Смешанные хозяйственные стратегии компаний и экономический рост

1. Введение в проблему

В настоящее время темпы экономических изменений возрастают, увеличивается динамичность институциональных и технологических сдвигов. В этой связи все более актуальными становятся исследования по установлению общих закономерностей трансформации как отдельных хозяйственных участников, так и целых экономических систем. Одним из плодотворных направлений такого класса исследований является экономическая теория, которую можно называть теорией экономических (хозяйственных) ловушек. Исторически методологические основы этой теории были заложены В.М.Полтеровичем в развитой им теории институциональных ловушек [1]. В дальнейшем было получено много интересных результатов применительно к отдельным видам институциональных ловушек. Однако наиболее интересными представляются максимально общие свойства систем, попавших в неэффективное состояние. Некоторые из этих свойств были раскрыты в работах [2-4]. Впоследствии в работе [5] было показано, что выявленные функциональные свойства экономических систем характерны не только для институциональной, но и для технологической составляющей экономических агентов. Справедливости ради следует заметить, что внутри рассматриваемого предприятия выявленные свойства могут носить как технологическую, так и институциональную окраску. Однако все экстернальные (рыночные) механизмы возникновения, поддержания и преодоления «ловушечных» состояний носят преимущественно институциональный характер.

Таким образом, эффекты и закономерности, изначально установленные для институциональной среды, действуют в более широком диапазоне хозяйственных явлений, включая технологические особенности хозяйственных участников. Следовательно, можно говорить о том, что во внутренней (сфере производства) и во внешней (сфере взаимодействия с другими участниками рынка) сферах деятельности компании действуют некие универсальные законы функционирования. Данный факт позволяет говорить либо о теории институциональных ловушек в широком смысле, которая с учетом экстернальных механизмов раскрывает трансакционные и технологические особенности функционирования компаний, либо об общей теории экономических ловушек. На наш взгляд, последняя этимологическая трактовка нынешнего положения дел в экономической теории более адекватна, в связи с чем в дальнейшем будем ее использовать в качестве рабочего понятийного аппарата.

В данной статье будут обобщены полученные в предыдущих работах [3-5] выводы о влиянии структуры хозяйственных операций на экономический рост. Так, если ранее эти выводы делались, исходя из гипотезы о неизменности структуры хозяйственных операций компании, то в настоящей статье эта гипотеза снимается, что и позволяет получить более полную и ясную картину рассматриваемых экономических процессов.

2. Смешанные хозяйственные операции: виртуальная и реальная оптимизация при фиксированном спросе

Рассмотрим ситуацию, когда хозяйственная структура работает в рамках двух хозяйственных укладов. Если рассматривать институциональные уклады, то в качестве примера можно привести фирму, осуществляющую сбыт своей продукции как в монетарной, так и в бартерной форме. Если же рассматривать технологические уклады, то примером может служить компания, осуществляющая производство своей продукции на старом и новом оборудовании одновременно. В обоих случаях разные хозяйственные уклады будут различаться величиной издержек, что и позволяет их рассматривать в рамках единой модельной схемы.

Таким образом, ключевым понятием для нас выступает «смешанная» хозяйственная стратегия компании, под которой понимается ситуация, когда производственная или маркетинговая деятельность фирмы ведется в рамках двух или более хозяйственных укладов одновременно. Для наглядности всех последующих построений будем рассматривать случай двух укладов.

Рассмотрим компанию, максимизирующую свою прибыль в условиях работы в рамках двух хозяйственных укладов. Соотношение для объема прибыли фирмы π имеет вид:

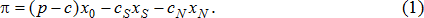
Если рассматривается смешанная технологическая стратегия фирмы, то c – удельные непроизводственные (трансакционные) издержки фирмы, а c_S и с_N – удельные производственные издержки фирмы в рамках старой и новой технологии соответственно. Если рассматривается смешанная институциональная стратегия компании, то показатель c несет нагрузку удельных производственных затрат предприятия, а c_S и с_N – удельных непроизводственных (трансакционных) издержек в рамках старого и нового институтов. Таким образом, изменение сферы, в рамках которой реализуются смешанные хозяйственные стратегии компании, ведет лишь к изменению интерпретации модельных переменных и не затрагивает саму аналитическую схему.

Теперь рассмотрим две задачи, которые приходится решать компаниям, работающим в рамках двух видов хозяйственных операций. Первая из них формулируется следующим образом: каков оптимальный объем операций в рамках старого (менее эффективного) хозяйственного уклада (x_S), обеспечивающий максимум чистой прибыли предприятия, при фиксированном спросе на производимую и реализуемую продукцию (то есть x₀ предполагается константой)?

Для определенности и конкретизации анализа предположим, что удельные текущие издержки каждой хозяйственной операции линейно зависят от объема производства:

Все входящие в формулы (2) и (3) параметры b_S, b_N, a_S и a_N положительны (это вытекает из существования эффектов масштаба и обучения dc_S/dx_S < 0 и dc_N/dx_N < 0).

Подставив выражения (2) и (3) в (1) с учетом, что x_N = x₀ - x_S, получим следующее соотношение:

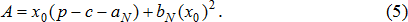
Из соотношения (4) несложно видеть, что зависимость прибыли от объема операций x_S представляет собой параболу, ветви которой направлены вверх. Тогда максимизация прибыли по x_S осуществляется на концах параболы. Таким образом, при фиксированном спросе на продукцию рассматриваемой компании ей невыгодно использовать два способа хозяйствования одновременно, а наоборот имеет смысл перейти к чистой стратегии, культивируя либо старый, либо новый способ хозяйствования. Следовательно, на начальной стадии принятия решения о целесообразных пропорциях между двумя хозяйственными укладами компании придерживаются чистых стратегий. Аналогичный вывод, основанный на теоретико-игровой схеме, был получен в [1] при рассмотрении бартерной ловушки.

Однако подобная безусловная оптимизация носит, как правило, виртуальный характер. Дело в том, что нами по умолчанию предполагалось, что предприятие может производить все свои операции в рамках одного из двух имеющихся укладов. Однако такое отнюдь не всегда возможно. Предположим, например, что спрос на продукцию фирмы возрастает и для его удовлетворения она приобретает и внедряет новое оборудование, более эффективное по сравнению со старым. Сам переход на двухукладный режим хозяйствования обусловлен невозможностью удовлетворения спроса при использовании только старых производственных мощностей. Однако и закупленная порция нового оборудования тоже не может покрыть имеющийся спрос на продукцию фирмы. В этом случае рассмотренная выше оптимизация теряет смысл и становится виртуальной (потенциальной), так как полный отказ от любого способа хозяйствования влечет за собой соответствующее падение прибылей.

Аналогичная проблема встает и при использовании двух институтов (норм). Например, перехода компании на полный бартер никогда не наблюдается, хотя бы потому, что какая-то часть операций фирмы должна производиться в денежной форме в целях оправдания ее существования. В данном случае жесткие технологические ограничения отсутствуют, но имеются правовые ограничения и ограничения партнеров фирмы на ее продукцию по тому или иному виду сделок.

Как же тогда модифицируется задача?

Ее можно сформулировать следующим образом: как влияет увеличение объема операций в рамках старого (менее эффективного) хозяйственного уклада (x_S) на чистую прибыль предприятия в условиях фиксированного спроса на производимую и реализуемую продукцию (x₀ предполагается константой)?

В этом случае анализ сводится к знаку производной dπ / dx_S. Оказывается, что результат зависит от того, на какой ветви параболы (4) мы находимся. Если x_S* – точка минимума искомой параболы, то при x_S < x_S* имеет место dπ/dx_S < 0; в противном случае имеем dπ / dx_S < 0. Таким образом, при достаточно большом объеме операций в рамках старого уклада его и дальше имеет смысл увеличивать для увеличения прибыли; при малой изначальной величине x_S ее целесообразно еще больше уменьшить.

Наиболее интересной является технологическая интерпретация выявленного эффекта: обновление производственных технологий должно производиться не малыми порциями, а достаточно большими партиями. Учитывая естественное неравенство π(x_S=0) > π(x_S=x₀), можно утверждать, что обновление не должно быть слишком уж масштабным, так как точка минимума x_S* смещена вправо.

Итак, процесс постепенного обновления производства при одновременной эксплуатации двух видов оборудования требует соблюдения определенных условий. Если указанные условия соблюдены, то новое оборудование будет использоваться в напряженном режиме при недозагрузке старого оборудования; в противном случае будет наблюдаться недозагрузка нового оборудования на фоне напряженного режима эксплуатации старого.

Раскрытая закономерность чрезвычайно любопытна, так как показывает, каким образом при наличии старого и нового оборудования может возникать парадоксальная ситуация, когда простаивание новых технологий оказывается выгодным с экономической точки зрения. Институциональная интерпретация аналогична.

Особый интерес представляет случай, когда прибыль может становиться отрицательной. Геометрически это означает, что парабола (4) пересекает ось абсцисс в двух точках – x_S1 и x_S2. Тогда ситуация усложняется из-за возникновения зоны убытков: x_S1 < x_S* < x_S2. Такие смешанные режимы являются вообще неэффективными. Подобный ход событий предъявляет еще более жесткие требования к обновлению технологий и институтов.

3. Структура хозяйственных операций и экономический рост: общий вид основных соотношений

Еще более интересной и важной является задача по определению влияния структуры хозяйственных операций фирмы на масштаб ее деятельности. Содержательно такая постановка задачи связана со случаем экзогенного роста спроса на продукцию компании. Как правило, наступление такого события считается желанным и благотворным для любой фирмы. Однако, как будет показано ниже, иногда сложившаяся нерациональная структура хозяйственных операций фирмы может блокировать расширение ее деятельности.

Как и ранее будем предполагать, что предприятие функционирует в режиме смешанных стратегий. Если спрос на рынке на продукцию фирмы растет, то она, стараясь покрыть его, будет увеличивать выпуск либо за счет равномерного увеличения загрузки обоих видов производственных мощностей, либо за счет более напряженной эксплуатации одного из них по сравнению с другим. Каковы же здесь закономерности?

Для понимания роли структуры хозяйственных операций в принятии решений о целесообразности роста производства и продаж компании рассмотрим условие dπ / dx₀ = 0, которое в нашем случае выступает в качестве условия хозяйственного равновесия. Чтобы представить это условие в развернутой форме введем в рассмотрение следующие параметры: ς – исходная доля производимой и реализуемой продукции в рамках старого хозяйственного уклада, то есть ς = x_S / x₀; μ – доля вновь производимой и реализуемой продукции в рамках старого хозяйственного уклада, то есть μ=dx_S / dx₀, где dx₀ = dx_S + dx_N. В данном случае мы предполагаем, что исходная структура хозяйственных операций компании не совпадает с той, которая складывается в процессе наращивания оборота и операций компании. Для явного учета этого факта целесообразно ввести еще один параметр: k=μ/ς.

Коэффициент k>0 выступает в качестве своеобразной характеристики степени консервативности хозяйственной стратегии компании при осуществлении наращивания своих операций. Так, если k=1, то руководство компании предельно консервативно и придерживается исходной структуры хозяйственных операций; если k=0, то компания осуществляет бескомпромиссный поворот в сторону нового хозяйственного уклада. Хотя теоретически k может принимать любые значения, для нас имеет интерес лишь его узкий интервал 0 ≤ k ≤ 1.

Используя естественные соотношения

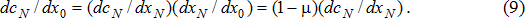
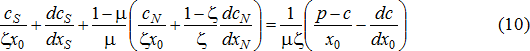
Задействовав коэффициент искажения структуры хозяйственных операций k, условие (10) можно свести к следующему уравнению относительно исходной доли хозяйственных сделок компании ς:

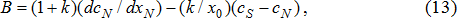
Если на практике при действующих параметрах имеет место ситуация, когда Aς₂ + Bς + U > 0, то рост производства и продаж фирме выгоден; в противном случае экономический рост компании приведет к падению ее прибылей. Таким образом, нарушение знака равенства в соотношении (11) в ту или иную сторону предопределяет характер дихотомии функционирования компании и влияние структуры ее сделок на возможный экономический рост.

Выведенное условие хозяйственного равновесия (11) является довольно сложным, так как коэффициенты (12)-(14) сами, как правило, зависят от структурного параметра ς. Конкретизация функциональной зависимости возможна при рассмотрении частных случаев связи между удельными издержками c_S (с_N) и объемом операций x_S (x_N).

4. Случай линейных издержек: теорема о смешанных хозяйственных стратегиях компании

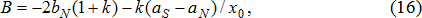
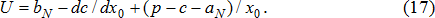
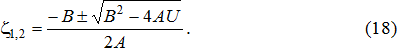
Учитывая, что dc / dx₀ < 0 несложно видеть, что параметры A и U всегда положительны, а параметр B при условии c_S > с_N всегда отрицателен. Это означает, что левая часть уравнения (11) представляет собой параболу, ветви которой направлены вверх. Следовательно, в общем случае рост операций фирмы целесообразен при доле ς, принадлежащей двум интервалам: [0;ς₁] и [ς₂;1] (с учетом того, что ς₁ < ς₂ и 0 < ς < 1).

Полученный содержательный результат можно сформулировать в виде теоремы о смешанных хозяйственных стратегиях компании.

Теорема: Если удельные издержки компании линейно зависят от объема хозяйственных операций, то при поддержании компанией одновременно двух видов хозяйственных операций наращивание ее рыночного потенциала (выпуска) является целесообразным только при условии, когда доля менее эффективной операции является либо достаточно малой, либо достаточно большой величиной.

Данная теорема подводит к пониманию той опасности, которая таится в самом факте смешанных хозяйственных стратегий. Наличие параллельных институтов и технологий, как оказывается, во многих случаях может препятствовать экономическому росту и провоцировать рецессию компании.

5. Коэффициент искажения структуры хозяйственных операций: роль операционной маневренности компании

Выведенные нами соотношения с одной стороны показывают роль структуры хозяйственных операций для жизненного цикла предприятия, а с другой – вскрывают роль фактора маневренности фирмы при переходе на новый хозяйственный уклад. Если первый фактор отображается переменной ς, то второй – параметром k. Оба указанных фактора тесно переплетены между собой. Так, изменение величины k приводит к деформации параболы и изменению зон роста и рецессии. В этой связи зададимся вопросом, как же влияет уровень консервативности компании в отношении существующих хозяйственных новшеств на их рыночные стратегии.

Прежде всего, заметим, что при k=1 имеет место полный консерватизм руководства компании в отношении существующих способов ведения хозяйственной деятельности. Это означает, что при осуществлении расширения своей деятельности компания в точности воспроизводит изначальную структуру хозяйственных операций. Если параметр k начинает отклоняться от единичной отметки в сторону уменьшения, то это свидетельствует о росте уровня адаптации предприятия к технологическим и институциональным новшествам. Если же коэффициент искажения структуры хозяйственных операций достигает точки k=0, то это свидетельствует об абсолютно бескомпромиссной политике фирмы в отношении внедрения инноваций. Иными словами, при k=0 хозяйственная структура «перекачивает» весь прирост производства и продаж на более эффективный способ ведения экономической деятельности.

Именно этот предельный случай k=0 и представляет для нас повышенный интерес, ибо посредством него мы можем установить роль исходной структуры хозяйственных операций при идеальном поведении экономического агента. Если сохранить предпосылку о линейности функций издержек, описываемых зависимостями (2) и (3), то из уравнения (11) легко получить следующее правило: если ς < ς*, то компании выгодно расширять свою деятельность; в противном случае рост оборотов компании приведет к падению ее прибылей. При этом критическая величина доли ς рассчитывается по следующей формуле:

Полученная формула довольно-таки интересна. Так, учитывая, что выражение в скобках всегда положительно, в соответствии с ней «опасная» доля старого хозяйственного уклада всегда больше 50%, то есть при высокой инновационной восприимчивости компании к имеющимся хозяйственным новшествам рост ее экономической деятельности блокируется только при явном доминировании старого хозяйственного уклада (ς > 50%). Помимо прочего, установленный факт позволяет определить и «зону безопасности» – ς < 50%. До тех пор, пока старый хозяйственный уклад оттягивает на себя меньше половины всего объема производства и продаж компании, до тех пор он не препятствует экономическому росту. Однако, как только пресловутая половина превышена, вероятность попадания компании в режим рецессии резко возрастает.

Выведенная формула (19) позволяет бросить общий взгляд на роль параметра k и нарисовать более полную картину его влияния на хозяйственные решения предприятия. Дело в том, что экстремальная точка (точка минимума) параболы (11) определяется по формуле: ς = -B / 2A. Для случая линейных издержек справедливо неравенство: dς / dk < 0.¹ С геометрической точки зрения это означает, что уменьшение k сдвигает точку экстремума параболы вправо, в сторону увеличения. При этом правая полоса сжимается и как бы «выдавливается» за пределы области определения ς, а левая полоса наоборот расширяется. Если данный процесс продолжается вплоть до момента, когда k=0, то точка экстремума оказывается за гранью ς=1, а на рисунке вместо трех полос остается только две. Тем самым высокая инновационная ориентация компании автоматически облегчает и упрощает процесс принятия решений о расширении экономической деятельности.

Особо подчеркнем тот факт, что даже при k=0 зависимость политики фирмы в отношении роста своих операций от их исходной структуры не исчезает. В любом случае имеется критическая точка для доли старого хозяйственного уклада, которая не должна быть превышена.

Теперь зададимся другим вопросом: а как влияет на процесс принятия решений вид функции удельных издержек? Сформулированная в предыдущем разделе теорема о смешанных хозяйственных стратегиях компании, разумеется, не является безусловным утверждением. Подчеркнем, что она справедлива лишь при линейной зависимости соответствующих удельных издержек от объемных характеристик произведенной и продаваемой продукции. Как же изменятся наши результаты, если вместо линейных функций (2) и (3) использовать гиперболические зависимости c_S = a_S + b_S / x_S и c_N = a_N +b_N / x_N?²

Оказывается, характер дихотомии будет задаваться следующим упрощенным правилом: если ς < ς*, то компании выгодно расширять свою деятельность; в противном случае – не выгодно. Критическая точка ς* оценивается по следующей формуле:

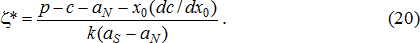
Из (20) видно, что в случае гиперболических издержек зависимость решений фирмы от структуры ее операций упрощается, в связи с чем корректируется и роль коэффициента k. Так, например, при k=0 расширение производства и сбыта компании всегда выгодно и не зависит от сложившейся структуры хозяйственных операций. Однако при k≠0 ситуация усложняется и структура хозяйственных операций начинает играть активную роль в формирования производственно-сбытовой политики фирмы. Таким образом, любое отклонение от бескомпромиссной инновационной стратегии и тяготение компании к своим прошлым решениям для поддержания сложившейся структуры хозяйственных операций активизирует и сам фактор структуры хозяйственных операций.

В целом же можно сделать любопытный вывод относительно роли геометрии удельных издержек: при повышении степени вогнутости кривых издержек влияние структуры хозяйственных операций на экономическую политику компании уменьшается. Иными словами это можно сформулировать так: чем более гибко реагируют удельные издержки на рост операций, тем больше свобода компании при выборе стратегии развития.

6. Смешанные хозяйственные стратегии как разновидность экономических ловушек

Рассмотренные в предыдущих разделах статьи эффекты, связанные с влиянием структуры хозяйственных операций на экономическую политику компании, имеют большое значение для понимания протекания переходных процессов и, прежде всего, процессов замещения одного хозяйственного уклада другим. В данном случае наиболее существенным для нас является тот факт, что функционирование предприятия в режиме смешанных хозяйственных стратегий может препятствовать экономическому росту. Во многих случаях доминирование старого хозяйственного уклада делает невыгодным расширение производственных и торговых операций фирмы. Относительно подобных ситуаций принято говорить, что на предприятии сложилась нерациональная структура производства и сбыта продукции, которая для данного предприятия превращается в своеобразную экономическую ловушку, которая может принимать форму институциональной или технологической ловушки.

Данные состояния правомерно считать ловушками, так как с одной стороны они неэффективны, ибо провоцируют рецессию компаний, а с другой – они могут стимулировать отказ производителя от новых форм хозяйственной деятельности в пользу менее эффективных старых. С формальной точки зрения это означает, что коэффициент искажения k будет выбираться таким образом, чтобы обеспечить выгодность роста фирмы (dπ / dx₀ > 0), а это во многих случаях возможно только при k>1, что равносильно подавлению удельного веса и роли нового хозяйственного уклада. В данной работе мы не рассматриваем условия, при которых происходит подобный возврат к старым институтам и технологиям, однако сама его возможность имеет принципиальное значение.

Насколько опасны смешанные хозяйственные стратегии?

На наш взгляд, ответ на этот вопрос требует отдельного и довольно тонкого исследования. Однако, учитывая механизм вытеснения старых хозяйственных укладов, можно утверждать, что смешанные хозяйственные стратегии способны оказывать депрессивный эффект, как правило, в краткосрочном периоде. Так, если на каждом шаге принятия решений руководство компании будет придерживаться правила перераспределения своих ресурсов с k<1, то через определенное число шагов доля ς уменьшится настолько, что уже не будет сдерживать экономический рост. Тем не менее, на протяжении некоторого переходного периода компания должна быть готова нести убытки. Разумеется, это всего лишь общая схема процесса, требующая детализации и уточнения.

Последнее, что хотелось бы подчеркнуть относительно полученных взаимосвязей между экономическим ростом и структурой хозяйственных операций компании, это их противостояние известному результату, который в экономической теории фигурирует как теорема Модильяни-Миллера. В соответствии с этой теоремой стоимость фирмы не зависит от структуры ее капитала [6]. Столь парадоксальный результат до сих пор вызывает споры и обсуждения. В нашем случае ситуация диаметрально противоположная: структура производства и реализации продукции фирмы в значительной мере предопределяет дальнейшие действия фирмы по производству и реализации продукции. Таким образом, закономерности, характерные для сферы управления финансами, нарушаются в сфере реального производства и сбыта.

7. Некоторые эмпирические подтверждения

Полученные теоретически закономерности функционирования предприятий нуждаются хотя бы в самой предварительной верификации. Найти в хозяйственной практике пример, который бы полностью отвечал всем условиям теоретической схемы, довольно трудно. Между тем некоторые аналогии иногда возникают. К их числу можно отнести интересный эмпирический результат в отношении приватизации в России. Так, в соответствии с исследованием Ю.В.Перевалова, И.Э.Гимади и В.В.Добродея, результаты приватизации существенно зависят от доли акций предприятия, находящихся в руках государства. Как оказывается, увеличение данной доли отрицательно сказывается на многих экономических показателях компаний, включая объем производства, только в том случае, когда она находится в интервале от 5 до 51% [7, с.6]; в противном случае активность компаний возрастает. Это означает, что для того, чтобы предприятие имело стимулы к росту, государство должно либо обеспечить себе контрольный пакет акций (более 50%), либо свести свое участие к минимуму (менее 5%), т.е. действовать на интервалах [0;0,05] и [0,5;1,0]. В промежуточной зоне возникает депрессивный эффект.

В описанном примере речь идет по сути дела о существовании некоей параболической зависимости относительно доли государственного (частного) института собственности, что очень напоминает обсуждаемый в данной статье эффект. Адаптируя «эффект приватизации» к нашей теоретической схеме, можно считать, что часть реализуемой продукции предприятия принадлежит частным лицам, а другая часть – государству. Хотя на практике жесткого разделения двух видов продукции не происходит, а все процессы происходят внутри самой компании, аналогия все же налицо. Тем самым есть основания полагать, что теорема о смешанных хозяйственных стратегиях компании не является чисто теоретической конструкцией, а имеет реальное значение для формирования производственных стратегий предприятий.

1. Полтерович В.М. Институциональные ловушки и экономические реформы// «Экономика и математические методы», Том 35, №2, 1999.
2. Polterovich V.M. Rent Seeking, Tax Policy and Economic Growth. New Economic School, Working Paper, 2001/027.
3. Балацкий Е.В. Непроизводственные издержки в теории институциональных ловушек/ В сб.: «Актуальные проблемы государственного строительства и управления». М.: ГУУ, 2000.
4. Балацкий Е.В. Функциональные свойства институциональных ловушек// «Экономика и математические методы», №3, 2002.
5. Балацкий Е.В. Экономический рост и технологические ловушки// «Общество и экономика», №11, 2003.
6. Модильяни Ф., Миллер М. Сколько стоит фирма? Теорема ММ. М.: Дело. 2001.
7. Перевалов Ю.В., Гимади И.Э., Добродей В.В. Анализ влияния приватизации на деятельность промышленных предприятий. М.: РПЭИ, 2000.

 

¹ Данный факт вытекает непосредственно из развернутого соотношения для ς*:

² Гиперболические функции издержек в каком-то смысле являются даже более естествен-ными, чем линейные. Например, на практике совокупные издержки фирмы CS описываются классическим соотношением C_S = b_S + a_Sx_S, где b_S – постоянные издержки производства, a_S – коэффициент роста переменных издержек, a_Sx_S– величина переменных издержек. Если данное соотношение разделить на x_S, то мы перейдем непосредственно к гиперболическим функциям удельных издержек c_S = C_S / x_S.