Рыночное ценообразование и производственные циклы

1. ВВЕДЕНИЕ

Одним из ключевых направлений исследований экономистов-теоретиков всегда был и остается механизм ценообразования. Однако, несмотря на это, в данной области все же еще остаются не до конца решенные вопросы. К числу таковых относится проблема синтеза двух аспектов ценообразования. Так, с одной стороны классическая теория фирмы утверждает, что в случае производственного равновесия цена выпускаемой предприятием продукции должна быть равна предельным издержкам. С другой стороны «паутинная» теория рыночного ценообразования говорит, что равновесная цена соответствует равенству спроса и предложения на рынке. Таким образом, одна теория изучает процесс ценообразования с точки зрения производителя, а другая – с точки зрения рынка и отчасти потребителя. Одна теория акцентирует внимание на процессах в сфере создания продукта, а другая – в сфере его реализации. Однако совершенно очевидно, что на практике эти два типа процессов протекают одновременно и, переплетаясь между собой, определяют динамику всей экономической системы. Между тем теории, увязывающей указанные стороны ценообразования в рамках единой схемы, до сих пор нет.

Тем не менее, сейчас хорошо просматриваются две линии исследований, которые позволяют подойти к решению поставленной проблемы. Так, с одной стороны уже предпринимались попытки построения синтетической схемы ценообразования, включающей затратный и рыночный аспекты [1]. С другой стороны накоплен большой опыт в исследовании производственных циклов на базе построения моделей динамических систем [2]. Однако здесь имеются определенные «неувязки». Например, теоретическая синтетическая схема ценообразования, рассмотренная в [1], носит слишком общий, преимущественно макроэкономический характер, а, главное, является статичной. Это предопределяет не слишком эффективные интерпретации разных частных случаев, которые имеют ключевое значение для понимания сути проблемы. В то же время ставшие уже классическими модели делового цикла, включая модели У.Чанга и Д.Смита, В.Торре, Г.Скинаси, Х.Роуза и Ж.-П.Бенасси [2], не включают в себя ценовые механизмы.

В настоящее время, на наш взгляд, ничто не мешает соединить рыночный механизм балансировки спроса и предложения и производственный механизм учета прибыли и издержек в рамках простой динамической модели. Этому вопросу и посвящена данная статья.

2. БАЗОВАЯ МОДЕЛЬ ДИНАМИКИ ПРОИЗВОДСТВА И ЦЕН

Здесь и далее будем рассматривать следующую динамическую модель, описывающую динамику цен и производства:

Поясним соотношения модели. Уравнение (1) представляет собой классическую модель рыночного ценообразования, часто фигурирующую в литературе в качестве модели П.Самуэльсона. В ее основе лежит «паутинная» схема формирования цены, основанная на механизме «нащупывания» точки равновесия между спросом и предложением: при D>Y цена возрастает, в противном случае – убывает. Уравнение (2) описывает механизм нащупывания производителем точки равновесия между ценой и предельными издержками по выпуску. В данном случае предполагается, что это равновесие постоянно нарушается, что и приводит в действие процедуру корректировки объема производства: если P>dC/dY, то прибыль PY - C(Y) производителя растет при увеличении выпуска и ему выгодно и наращивать производство, в противном случае ему следует сокращать производственную активность.

В основе построенной модели (1)-(2) лежит ряд упрощающих анализ предпосылок. Во-первых, в ней рассматривается монопродуктовое производство. Во-вторых, речь идет о локализованном рынке сбыта, когда все предложение продукта формируется одним производителем. Возможна и другая интерпретация, когда предложение товара определяется групповым производителем, но тогда уравнение (2) описывает также производство группы предприятий. В-третьих, нами моделируется «смешанный» механизм ценообразования, когда производитель и продавец товара выступают в одном лице и производитель является частично прайс-тейкером (пассивно учитывает рыночные цены), а частично прайс-мейкером (сам участвует в их формировании). На наш взгляд, указанные допущения не являются настолько сильными, чтобы построенная на их основе модель генерировала ошибочные или неточные содержательные выводы.

Основным достоинством модели (1)-(2) является именно уравнение (2). Насколько нам известно, несмотря на его простоту и очевидность, оно еще ни разу в явном виде не фигурировало в модельном анализе и тем более в связке с ценовой моделью П.Самуэльсона. Благодаря уравнению (2) в схему ценообразования вводится не только спрос и предложение, но и затратный (технологический) фактор производства. Это позволяет исследовать производственные траектории различных типов предприятий (с разной эластичностью издержек по выпуску) в условиях рыночного ценообразования.

Разумеется, уравнения (1) и (2) представляют собой частные и самые простые случаи механизмов нащупывания экономического равновесия. В принципе можно рассмотреть и различные модификации указанных механизмов. Например, вместо модели П.Самуэльсона можно использовать известную модель Ф.Дрэша [3]. Можно использовать и нелинейные связи между переменными. Вообще говоря, модель (1)-(2) можно было бы расширить путем введения еще одного уравнения, описывающего динамику спроса. Однако в первом приближении можно остановиться на построенной модели для уяснения ключевых закономерностей взаимовлияния механизма рыночного ценообразования и процесса производства.

Целью дальнейшего анализа является изучение динамических свойств производства в условиях рыночного ценообразования. Особый интерес здесь представляет рассмотрение разных типов производства: с высокой и низкой эластичностью издержек по выпуску. Кроме того, наш пристальный интерес будет сосредоточен на выяснении условий возникновения колебаний выпуска, ведущих к возникновению производственных циклов.

3. АНАЛИЗ МОДЕЛИ: СЛУЧАЙ ФИКСИРОВАННОГО СПРОСА

Для упрощения формального анализа предположим, что рыночный спрос является фиксированным: dD / dt = 0. Речь идет о том, что спрос задан экзогенно и не зависит от цен. Данный постулат является неоднозначным. Дело в том, что, хотя нет сомнений в том, что цены влияют на спрос, имеется много случаев, когда можно наблюдать довольно интересную картину: спрос формируется по каким-то своим внутренним законам, основанным на потребностях людей, и почти никак не связан с ценами. Впоследствии мы рассмотрим и случай эндогенного спроса как функции цен, но пока остановимся на предпосылке о его неизменности.

Проведем качественный анализ системы (1)-(2) с учетом сделанного предположения. При этом не будем вдаваться в формальные детали этого анализа, а сконцентрируем внимание на характере влияния технологической спецификации производства на поведение системы (1)-(2).

Якобиан (J) системы (1)-(2), в том числе в особых точках, равен: J = βγ > 0. Следовательно, особая точка системы заведомо не является седловой, а сама система не является принципиально неустойчивой. Из анализа дивергенции модели (1)-(2), которая равна div(P,Y) = -γC", вытекают следующие представления о поведении системы.¹ При c" > 0 особая точка (P*;Y*) устойчива²; при c" = 0 особая точка, скорее всего, является центром и в системе возникают периодические незатухающие колебания; при c" < 0 особая точка становится неустойчивой. Мы не проводим окончательную идентификацию особых точек типа центра, фокуса и узла, т.к. полученного результата нам достаточно для уяснения характера воздействия затратных свойств производства на динамику системы (1)-(2). В данном случае мы видим, что пропорциональные (линейные) издержки провоцируют постоянные флуктуации цен и производства. При возникновении позитивного эффекта масштаба производства (c" < 0) циклические флуктуации «искривляются» и динамика системы еще больше усложняется. Если же мы имеем дело с ресурсоемким производством (c" > 0) с опережающим ростом издержек по сравнению с выпуском (т.е. в системе доминирует закон падающей отдачи факторов производства), то, как оказывается, в системе возникает стабилизирующий эффект.³

Таким образом, традиционный постулат экономической теории о снижении удельных издержек при росте выпуска под воздействием эффекта масштаба производства имеет важное следствие в виде дестабилизирующего влияния на динамику цен и производства. В связи с этим имеет смысл остановиться на кратком обсуждении данного постулата. Дело в том, что в соответствии с неоклассической теорией фирмы достаточным условием оптимальности объема выпуска является условие c" > 0 [4]. Однако на самом деле это очень сильное условие, которое отнюдь не всегда имеет место в реальности. Более того, если увеличение издержек происходит таким образом, что все ресурсы (факторы) производства увеличиваются пропорционально, то данное условие не выполняется, т.к. оно вступает в противоречие с эффектом масштаба производства. Если мы имеем дело с линейно однородной производственной функцией, степень однородности которой больше единицы, то эффект масштаба выполняется автоматически. Возможна и обратная ситуация, когда степень однородности производственной функции меньше единицы. Именно этот случай и рассматривается неоклассической теорией фирмы в качестве типичного.

Следует отметить также, что для динамической постановки задачи и, в частности, для уравнения (2), гипотезы о знаке второй производной C", вообще говоря, не имеют принципиального значения. Так, если при C" < 0 неоклассическая задача фирмы теряет содержательный смысл, то модель (1)-(2) сохраняет свою логику и реалистичность.

После сделанных замечаний можно перейти к анализу частного, но важного случая, когда издержки задаются квадратичной функцией выпуска:

Подобная спецификация затрат обусловлена тем, что позволяет очень хорошо отобразить свойства выпуклости и вогнутости функции и, следовательно, эффект масштаба производства. Одновременно с этим конкретный вид функции (3) позволяет получить все решения модели (1)-(2) в явном виде. Для этого редуцируем систему (1)-(2) к следующему уравнению относительно Y:

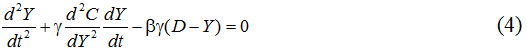
Учитывая упрощающие допущения, уравнение (4) сводится к обыкновенному неоднородному дифференциальному уравнению второго порядка:⁴

В общем случае решение уравнения (5) имеет вид:

Зависимости (9) и (10) находятся из начальных условий:

При выполнении условия γa² < β в системе возникают циклические колебания, а решение уравнения (5) приобретает следующий вид:

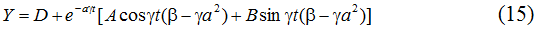
Отсюда непосредственно видно, что при C" < 0 и, следовательно, при a < 0, в системе идут нарастающие колебания. Таким образом, эффект масштаба производства при соответствующих условиях ведет к дестабилизации динамики самого производства и цен. Если же действует сильный закон падения эффективности производственных ресурсов С" > 0, то колебания в системе становятся затухающими. Данный вывод находится в согласии с предшествующим качественным анализом системы (1)-(2). Кроме того, при С" = 0 циклы в системе возникают безальтернативно, что подтверждает ранее сделанный вывод о том, что в данном режиме особая точка модели (1)-(2) является центром.

Функция (15) может быть представлена в следующем, более компактном виде [5]:

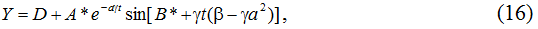
Отсюда можно в явном виде определить длительность периода колебаний T [6]:

Из соотношения (17) хорошо просматривается влияние каждого параметра на частоту колебаний и длительность производственного цикла. Прежде всего, видна следующая закономерность: чем выше чувствительность процесса «паутинного» ценообразования, тем короче производственный цикл и тем чаще неустойчивее динамика выпуска продукции. Одновременно с этим действует другая интересная зависимость: чем больше выпуклость кривой издержек (причем неважно, в какую сторону), тем больше длина производственной волны. Иными словами, чем сильнее выражена нелинейность кривой издержек и соответственно ее отклонение от прямой линии, тем устойчивей производственная динамика. Несколько сложнее обстоит дело с параметром чувствительности γ. Оказывается для него имеется критическая точка

Более тщательный анализ решения (6) показывает, что в системе может возникать и гладкий рост производства без «перегибов» кривой (6) во времени. Однако для этого требуются довольно жесткие условия. В частности, при C" < 0 характеристические корни (7) и (8) положительны и λ_S > λ_F. Тогда монотонный рост производства происходит при положительности обеих постоянных интегрирования (9) и (10), что возможно только при выполнении следующих начальных условий:

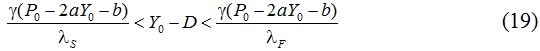
Таким образом, устойчивый рост возможен только, если изначальное неравновесие на рынке между спросом и предложением не слишком мало и не слишком велико. В остальных случаях, когда для нашего случая постоянные интегрирования имеют разный знак, на кривой Y(t) образуются либо «горбы», либо «ямы» с вершиной в точке

Следовательно, в большинстве случаев образуется «неправильная» волна, которая может трактоваться как иррегулярный производственный цикл.

Примечателен следующий факт: выполнение условия возникновения циклический колебаний γa² < β не зависит от знака C". Иными словами, система срывается в устойчивый колебательный режим не в зависимости от характера кривизны функции издержек (выпукла она или вогнута), а от степени ее кривизны (насколько сильно она выпукла или вогнута). При этом прослеживается следующая закономерность: при │C"│ > 1 слишком гибкое рыночное ценообразование с большим значением параметра β провоцирует нарушение стабильности в системе; если │C"│ < 1, то циклы рождаются при слишком активной реакции производителя на ценовое неравновесие с большим значением параметра γ. Можно сказать, что в зависимости от абсолютной величины C" источники нестабильности системы меняются местами.

Остановимся на экономико-математической интерпретации данного вывода. Казалось бы, более эффективное производство должно стабилизировать производственный процесс, почему же происходит обратное? На самом деле выявленный эффект является вполне естественным. Допустим, имеет место ситуация C" < 0. Тогда стационарная точка кривой издержек является точкой минимума. Если в этом случае цена выше предельных издержек производителя, то он будет увеличивать свой выпуск, удаляясь от стационарной точки, являющейся своеобразной точкой притяжения. Возможно, что в этом случае процесс роста производства будет идти с определенным ускорение. Кроме того, сам рост оказывается неограниченным, т.к. естественный ограничитель в виде стационарной точки остался позади – производитель ее уже проскочил. При C" > 0 стационарная точка является точкой максимума. Если цена выше предельных издержек производителя, то начинается рост выпуска в направлении стационарной точки притяжения. Данная точка является естественным ограничителем роста, и по мере приближения к ней будет наблюдаться некоторое замедление процесса. Таким образом, условие C" < 0 в отличие от условия C" > 0 стимулирует ничем не ограниченные сдвиги в выпуске, а это в свою очередь приводит к более мощному рывку в динамике цен на рынке и т.д. Тем самым наличие эффекта масштаба производства инициирует более «размашистые» действия производителя, что и является источником нестабильности всей системы.

4. АНАЛИЗ МОДЕЛИ: СЛУЧАЙ ЭКЗОГЕННОГО СПРОСА

Рассмотрим более общий случай, когда рыночный спрос формируется под воздействием каких-то экзогенных причин и задается некоей функцией времени. Для определенности предположим, что он растет с постоянным темпом r: D = D₀e^rt, где D₀ – спрос в начальный момент времени. Тогда уравнение (5) немного усложнится и примет вид:

В этом случае решение уравнения (21) имеет вид:

Отсюда видно, что при r>0 слагаемое ψ<0 при λ_F < r < λ_S. В противном случае ψ>0, т.е. когда темп роста спроса либо слишком мал, либо слишком велик. Отсюда вытекает интересный парадокс: казалось бы, растущий спрос должен однозначно стабилизировать производство и способствовать его росту, однако, как оказывается, это отнюдь не всегда так.

Таким образом, при экзогенном спросе в системе возникает дополнительный фактор «искривления» производственной кривой. В частности, ярким случаем является ситуация, когда выполняется условие (19) и система с фиксированным спросом находится в режиме стабильного производственного роста. Если при этом спрос оказывается экзогенно растущим и выполняется условие λ_F < r < λ_S, то ψ<0 и траектория (22) деформируется в направлении образования производственного цикла – ямы или горба в зависимости от начальных условий.

Рассмотренный случай показывает еще один возможный источник нестабильности системы в виде спроса. Переплетение спроса с другими свойствами системы может приводить к неочевидным последствиям.

5. АНАЛИЗ МОДЕЛИ: СЛУЧАЙ ЭНДОГЕННОГО СПРОСА

Следующим шагом в усложнении исходной модели (1)-(2) является введение эндогенного спроса, зависящего от цены. В частном, наиболее простом случае можно задать функцию спроса в следующем виде: D = K / P, где K – доход потребителя в денежной форме, идущий на приобретение производимого товара. Однако даже при такой простой связи получающаяся система уже не может быть сведена к одному уравнению более высокого порядка. Данный момент является принципиальным, ибо рассматриваемая система, как оказывается, может быть исследована в явной форме только при наличии двух уравнений и двух взаимосвязанных факторов: производства и цен. Попытка интегрировать в систему фактор спроса, зависящего от цен, позволяет проводить только качественный анализ модели. Указанное расширение исходной модели делает детальный анализ ее траекторий невозможным, а сама система становится информационно избыточной и в методическом плане «зацикленной».

В дальнейшем для нас вполне удобно рассмотреть функцию спроса в общем виде как функцию цены: D = D(P). Здесь, как и раньше, мы наметим лишь самые общие контуры качественного анализа, не вдаваясь в формальные строгости. Это связано с тем, что, во-первых, мы хотим уяснить принципиальную роль спроса и технологической специфики производства, а во-вторых, даже проведя скрупулезный анализ, мы все равно не получим аналитических решений в явной форме.

Введя понятие эластичности спроса по цене E=(P/D)(dD/dP), якобиан системы (1)-(2) при произвольной функции спроса можно записать в виде:

Если сделать естественное предположение, что E<0, то легко видеть, что при выполнении условия C" / ED > C", т.е. при достаточно сильном эффекте масштаба производства, особая точка системы является седловой, и в системе возникают колебания производства и цен. Если данное условие нарушается или если C" > 0, то устойчивость системы повышается.

Если выполняется условие

Особо следует отметить следующий момент. Нами рассматривались убывающие кривые спроса. Однако, как известно, иногда возникает так называемый гиффиновский эффект, когда E>0⁶. В этом случае все сделанные нами выводы переворачиваются на прямо противоположные: эффект масштаба производства и низкая эластичность спроса увеличивают устойчивость системы.

6. ЗАКЛЮЧЕНИЕ

Построенная модель (1)-(2) позволяет соединить две стороны ценообразования: затратную и рыночную. Кроме того, данное объединение происходит в рамках динамической схемы механизма нащупывания системой экономического равновесия. Это уже само по себе можно считать определенным продвижением вперед по пути построения более комплексной теории ценообразования и производственных циклов.

Рассмотрим указанные моменты более подробно.

Во-первых, нами была выполнена «динамизация» статической теории фирмы, которая не рассматривает реальные адаптивные механизмы действий производителя.

Во-вторых, указанная динамизация теории фирмы была дополнена рыночным механизмом ценообразования. Это позволило учесть фактор рыночного спроса и степень гибкости рыночных цен.

В-третьих, построенная модель позволила принципиально «расширить» статическую теорию фирмы, которая традиционно исключает из рассмотрения случай, когда предельные издержки убывают по мере роста производства. Такое игнорирование случая c" < 0 приводило к отсечению от экономической теории огромного класса производственных объектов, для которых имеет место положительный эффект масштаба производства.

В-четвертых, модель (1)-(2) позволила установить, как влияет производственно-технологическая специфика предприятия, задаваемая свойствами кривой издержек и, в частности, условиями c" < 0 и c" > 0, на динамику выпуска и цен. Зависимость производственных и ценовых циклов от вида кривой издержек, на наш взгляд, является относительно новым теоретическим результатом. Кроме того, было выяснено, что активный эффект масштаба производства (c" < 0) оказывает дестабилизирующее влияние на траектории цен и производства. Была дана также содержательная экономико-математическая интерпретация причин «подталкивания» системы к неустойчивым режимам под воздействием эффекта масштаба производства.

В-пятых, был уточнен характер влияния экзогенного и эндогенного спроса на поведение системы. В частности, показано, что экзогенно растущий спрос при определенных условиях может отрицательно действовать на производственную динамику и приводить к образованию апериодических производственных циклов. Кроме того, для эндогенного спроса, зависящего от цены, уточнены возможные режимы функционирования системы для двух важнейших классов товаров: обыкновенных (E<0) и гиффиновских (E>0).

Предложенная модель (1)-(2) предполагает развитие и обобщение. Например, ее можно дополнить уравнением, описывающим динамику спроса в зависимости от цен и дохода, и уравнением, описывающим динамику дохода в зависимости от выпуска. Можно ввести в рассмотрение ожидания цен и спроса, а также использовать более сложные стратегии поведения производителей, включая их отношение к неопределенности и т.п. Однако в любом случае анализ таких моделей в подавляющем большинстве случаев может быть проведен только на качественном уровне.

1. Балацкий Е.В. Издержки и полезность как факторы ценообразования// «Вестник Московского университета. Серия 6, экономика», №4, 2000.
2. Поманский А.Б., Трофимов Г.Ю. Математические модели в теориях экономического цикла// «Экономика и математические методы», Т.25, №5, 1989.
3. Klein L.R., Preston R.S. Stochastic nonlinear models// «Econometrica», Vol.37, No.1. 1969.
4. Интрилигатор М. Математические методы оптимизации и экономическая теория. М.: Прогресс. 1975
5. Выгодский М.Я. Справочник по высшей математике. М.: Физматгиз. 1963.
6. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. М.: Наука. 1986.