Моделирование и прогнозирование валютных курсов является чрезвычайно сложной проблемой. Почему? В связи с чем возникают непреодолимые трудности? Что необходимо учитывать при исследовании валютной динамики? Какие подходы могут быть предложены для преодоления инструментальных проблем?
В настоящее время проблема моделирования и прогнозирования динамики валютных курсов стоит по-прежнему достаточно остро. Это связано с глобальными сдвигами в мировой экономике. Во-первых, на арену вышла новая мировая валюта – евро. Недолгая история его существования показывает, насколько не простыми оказались его отношения с долларом, а также насколько жесткой может идти борьба между странами за удержание определенного валютного курса. Во-вторых, развитие международного рынка капитала и либеральной системы плавающих валютных курсов привело к полной потере ориентиров в отношении возможной динамики валютных курсов. В-третьих, к мировой валютной системе подключаются «новые» страны с так называемой переходной экономикой, обладающие весьма специфическими условиями и механизмами формирования валютного климата.
Указанные факторы актуализируют проблему выбора модельно-теоретического инструментария, способного хоть как-то сориентировать и отдельных экономических агентов, и целые государства в отношении возможных сдвигов в величине валютных курсов. Однако, чтобы сделать обоснованный выбор, необходимо проанализировать недостатки имеющихся подходов. Остановимся на моделях, учитывающих фундаментальные факторы формирования валютных курсов.
1. Недостатки существующих модельно-теоретических схем формирования валютных курсов
1. Классическая теория паритета покупательной силы. Одним из направлений моделирования и теоретического объяснения динамики валютных курсов является классическая теория паритета покупательной силы (ППС), смысл которой сводится к простому соотношению
Однако в такой форме теория ППС, помимо всего прочего, имеет тот кардинальный недостаток, что не учитывает обратные связи в экономической системе. Действительно, уровень валютного курса зависит от уровней цен в рассматриваемых странах, однако он же сам в значительной мере определяет уровень цен внутри страны. Например, для России валютный курс являлся и продолжает являться своеобразным «инфляционным якорем», так как цены на импортные товары, доля которых в стране составляет примерно половину всего потребительского рынка, жестко привязаны к курсу (с учетом надбавки за проведение импортных операций). Кроме того, сдвиги в динамике курса могут приводить к серьезным сдвигам в преференциях населения в отношении валютной структуры сбережений. Например, в России обесценение национальной валюты приводило к осознанию целесообразности хранения денежных средств в банкнотах США, а не в рублях, что еще больше стимулировало спрос на иностранную валюту и рост цен в стране.
Таким образом, теория ППС однобоко воспроизводит процесс формирования валютных курсов и не позволяет понять механизм самоподдерживающегося режима их роста. Между тем для нестационарных систем и, особенно, для переходных экономик такой механизм имеет принципиальное значение. Достаточно указать, что этот механизм лежал в основе инфляционного хаоса первых лет экономических реформ в России, которая к тому времени имела соотношение внутренних цен на продукцию добывающей и обрабатывающей промышленности намного ниже, чем в развитых капиталистических странах. Достижение структурно-ценового паритета российское правительство попыталось осуществить в 1992 г. путем административного (принудительного) повышения цен на продукцию топливно-энергетического комплекса. Однако такие действия не решили поставленной задачи из-за запуска механизма, нейтрализующего рост внутренних цен. Общая схема его такова: рост внутренних цен на продукцию топливно-энергетического комплекса стимулировал рост цен в остальных секторах экономики; возникший инфляционный импульс приводил к нехватке платежных средств и необходимости денежно-кредитной эмиссии; в полном соответствии с классической теорией ППС инфляция и рост рублевой денежной массы вели к девальвации рубля; возросшие внутренние цены на энергоресурсы, пересчитанные по упавшему валютному курсу рубля, оказывались приблизительно на прежнем уровне2. Далее указанный цикл повторялся, приводя к бесконечной эскалации инфляции и девальвации рубля.
Сказанное подводит к выводу, что выбрать классическую модель ППС в качестве ведущей при исследовании динамики валютного курса нельзя. Как было указано выше, это связано с тем, что в ней эндогенный механизм «валютный курс–внутренние цены» заменяется на одностороннюю связь, в которой цены выступают в качестве экзогенного фактора формирования курса.
2. Монетаристская теория паритета покупательной силы. Попытка «спасти» классическую теорию ППС путем придания ей явной монетаристской окраски не решает проблемы. В этом случае динамика валютного курса описывается следующим соотношением:
В основе этой модели лежит представление о том, что внутренние цены зависят от динамики денежной массы. Несмотря на то, что в принципе этот тезис является справедливым, его использование в конкретной модели может приводить к серьезным ошибкам. Так, например, в Японии после начала финансового кризиса в Юго-Восточной Азии денежная масса была увеличена на 60%, однако это не привело к инфляции и заметному падению курса иены3. Следовательно, при соблюдении определенных условий в экономику можно эмитировать довольно большие суммы денежных средств без вреда для национальной валюты. (Для сравнения: в России с августа 1998 г. до конца 1999 г. объем денежной массы возрос вдвое, а курс рубля упал в 4 раза4, т.е. в отличие от Японии эластичность курса по денежной массе в России была чрезвычайно высока). Это в свою очередь означает, что монетаристская модель ППС слишком грубо отражает взаимодействие валютного курса и денежных агрегатов. Хотя наличие связи между указанными характеристиками никем не оспаривается, механизм их переплетения, по-видимому, гораздо сложней, чем это постулируется монетаристской моделью ППС и ее модификациями.
Таким образом, опереться на монетаристскую модель ППС при исследовании динамики валютных курсов не представляется возможным. Пожалуй, особые трудности в использовании данной теории возникают для экономик с хорошо отлаженным эмиссионным механизмом и эффективной банковской системой.
3. Неравновесная теория паритета покупательной силы. Основой двух предыдущих теорий является постулат о равенстве валютного курса и паритета покупательной способности. Однако в реальности такое равенство почти никогда не наблюдается. Более того, динамика расхождения валютного курса и ППС уже стала самостоятельной научной проблемой. Данный факт стимулировал создание неравновесных теорий ППС.
Если ввести в рассмотрение относительный коэффициент валютного неравновесия
Данная модель основана на, казалось бы, естественной предпосылке стремления системы к равновесию. В соответствии с ней любое рассогласование между валютным курсом и ППС приводит в действие механизм перелива иностранной валюты, направленный на восстановление равновесия. Однако, как показывают последние исследования, на пути к пресловутому равновесию стоят определенные барьеры. Остановимся на этом моменте более подробно.
Соотношение между валютным курсом и ППС изучается давно. В частности, был установлен так называемый эффект Б.Балаша5, в соответствии с которым отношение паритета к курсу в разных странах сильно различается и снижается по мере сокращения душевого ВВП6. Еще в начале 70-х годов было замечено, что указанный эффект подчиняется довольно жесткой регрессионной зависимости. К настоящему моменту подобные расчеты «обновлены» В.А.Волконским и А.И.Кузовкиным на основе отчетных данных за 1998 г. по 106 странам мира. Результатом таких масштабных исследований стала следующая эконометрическая закономерность:
В соответствии с эконометрической закономерностью Волконского-Кузовкина при переходе к более бедным странам (росте g) происходит рост коэффициента рассогласования (Ω) между валютным курсом и паритетом покупательной силы. Иными словами, чем беднее страна, тем дороже для нее иностранная валюта.
Любопытно, что данный эмпирический факт имеет и строгое теоретическое обоснование. Так, например, Г.Ю.Трофимовым была построена модель общего равновесия, из которой явствует, что в условиях несовершенной конкуренции, когда число хозяйственных участников (экспортеров и импортеров) невелико, рассогласование между валютным курсов и ППС наблюдается практически всегда7. Данный факт позволяет добавить недостающее логическое звено в схему формирования динамики обменного курса: чем беднее страна, тем меньше в ней конкурентов, тем дальше экономические условия хозяйствования от совершенной конкуренции и тем дальше номинальный курс от ППС.
Рассмотренный эконометрический результат, вообще говоря, противоречит модели А.А.Первозванского. Причем это противоречие идет по нескольким направлениям. Рассмотрим их более подробно.
Во-первых, А.А.Первозванский исходил из того, что механизм возникновения и ликвидации рассогласования между валютным курсом и ППС целиком и полностью формируется внутри рассматриваемой страны. Эконометрическая закономерность Волконского-Кузовкина отвергает этот постулат, так как в соответствии с ней расхождение между валютным курсом и ППС зависит не только от самой страны, но и от всей мировой экономики. Более строго, указанное расхождение зависит от места страны в иерархии стран мировой экономики. Тем самым в модели не учитывается, с одной стороны, некий фактор валютного диспаритета в виде уровня жизни в стране, а с другой стороны, некий экзогенный фактор в лице эталонного уровня жизни (в частности, в США).
Во-вторых, модель А.А.Первозванского оперирует точкой равновесия, равной Ω=1, к которой сходится процесс. Между тем из закономерности Волконского-Кузовкина вытекает, что подобная «точка притяжения» может иметь место только для стран с уровнем жизни, примерно равным американскому эталону. К числу таких стран относятся Япония, Канада, Австралия, Гонконг, Сингапур и страны Западной Европы. Однако Россия к этой группе не принадлежит и для нее характерна совсем другая точка равновесия.
В-третьих, в модели А.А.Первозванского точка равновесия предполагается величиной, не изменяющейся с течением времени. Однако из регрессии Волконского-Кузовкина следует, что с изменением относительного уровня жизни в стране изменяется и точка равновесия, к которой будет стремиться величина расхождения Ω. Таким образом, точка равновесия является «плавающей» величиной, что, конечно же, придает более сложный рисунок процессу «нащупывания» равновесия между валютным курсом и ППС.
Таким образом, применить простейшую неравновесную теорию ППС к процессу формирования валютного курса нельзя. Особенно актуально это для стран с уровнем жизни, сильно отличающимся от эталонного (американского).
4. Концепция торгового баланса. Еще одним важным направлением объяснения динамики валютных курсов является концепция, в соответствии с которой величина валютного курса определяется торговым балансом страны или, что то же самое, соотношением импорта и экспорта. Типичным примером такого рода моделей может служить эконометрическая зависимость Ю.В.Ермолаевой8:
Хотя в общем случае отрицать подобную зависимость нельзя, в ряде особых случаев ее использование неправомерно. Недостаток концепции торгового баланса такой же, как и теории ППС, то есть она не учитывает обратные связи в экономической системе. Действительно, уровень валютного курса зависит от соотношения импорта и экспорта в рассматриваемой стране, однако он же сам в значительной мере определяет внешнеторговую активность. В этой связи интересно исследование В.А.Евсеева, показавшее сильную зависимость динамики импорта и экспорта от соотношения ППС к валютному курсу (в прежних обозначениях 1/Ω). Рассмотрим данный эффект более подробно.
Проведенные исследования позволили установить, что коэффициент 1/Ω имеет верхнюю и нижнюю планки. Так, если величина 1/Ω превышает 60%, то это приводит к резкому сокращению экспорта; если 1/Ω становится меньше 30%, то «режется» импорт9. Однако сильная деградация одного из внешнеторговых агрегатов быстро ведет к деградации другого и затуханию внешнеторгового обмена. И хотя соотношение между импортом и экспортом в этом случае может мало измениться, валютный курс, как правило, оказывается подвержен катастрофическим колебаниям. При этом даже если соотношение между импортом и экспортом впоследствии полностью придет в норму, то значение валютного курса, как правило, уже не восстанавливается. Такое развитие событий не вписывается в классическую схему торгового баланса.
Сказанное означает следующее. Модели торгового баланса могут применяться только в диапазоне «полосы В.А.Евсеева», когда 30%<1/Ω<60%. Если отношение ППС/курс выходит за эти пределы, то обратное влияние курса на внешнеторговый баланс возрастает настолько, что пренебречь им принципиально нельзя. Следовательно, валютный курс для России является не только «инфляционным якорем», но и своеобразным «внешнеторговым якорем». По ориентировочным оценкам В.А.Евсеева, для России полоса эффективных значений, когда в валютной сфере не наблюдается сильных возмущений, оказывается довольно узкой – 40%<1/Ω<45%. По-видимому, только в этих рамках возможно эффективное применение эконометрических зависимостей курса, основанных на учете объемов экспорта и импорта.
Таким образом, слепое использование моделей торгового баланса при исследовании динамики валютных курсов представляется довольно рискованным. Особые трудности в применении концепции торговых балансов возникают для экономик, находящихся в кризисном или предкризисном состоянии.
5. Модели биржевых торгов. Чрезвычайно важным подходом, направленным на исследование динамики валютных курсов в краткосрочном аспекте, является идея формирования обменного курса на основе биржевого механизма. Наиболее плодотворной попыткой формализации этой идеи применительно к российской ситуации может считаться модель биржевых валютных торгов, предложенная Ю.П.Лукашиным и А.С.Лушиным10. В общем виде эта модель выглядит следующим образом:
Данная модель практически никак не стыкуется с моделями динамики валютных курсов, рассмотренными нами ранее. Это и понятно, так как модель Лукашина-Лушина работает на принципиально более коротких временных интервалах. Однако даже для краткосрочных эффектов модель Лукашина-Лушина может быть применена отнюдь не всегда.
Как справедливо отмечается в литературе11, в этой модели имеется существенный недостаток из-за того, что в ней опять-таки отсутствует обратная связь между золотовалютными резервами Центрального банка (ЦБ) страны и осуществляемыми им валютными интервенциями. Фактически в данной модели золотовалютные запасы ЦБ предполагаются «бездонными»; в лучшем случае они выступают в качестве экзогенного агрегата. Такой подход приводит к тому, что модель не учитывает возможного истощения резервов ЦБ и возможной импульсной девальвации национальной валюты. Кроме того, импульсный эффект может возникнуть в результате «перелива» денежных средств с фондового рынка на валютный рынок. Таким образом, важным недостатком модели Лукашина-Лушина является автономное рассмотрение валютного рынка, в то время как биржевой механизм формирования валютного курса является единым и должен учитывать все составляющие финансового рынка. Возможные эффекты взаимного перелива денежных средств между фондовым и валютным рынками в рамках биржевого механизма единого финансового рынка существенно ограничивает предсказательные возможности рассмотренной модели биржевых торгов.
С эконометрической точки зрения модель Лукашина-Лушина ориентирована на исследование «малых» флуктуаций в динамике валютного курса. Например, коэффициент пропорциональности в ней меняется в зависимости от того, падающим или возрастающим является валютный курс. Таким образом, даже небольшие «откаты» валютного курса вниз модель Лукашина-Лушина воспринимает плохо, взрывные же эффекты курса (неважно, вверх или вниз) она и вовсе не «чувствует».
Похоже, что теоретико-модельный подход к учету возможных «незапланированных» импульсных эффектов в динамике валютных курсов уже не оправдывает себя. На наш взгляд, теоретические модели нуждаются в помощи со стороны прикладных эмпирических методов. Надо сказать, что последние сейчас выделились в самостоятельное направление экономических исследований и сейчас находятся в стадии бурного развития. Так, по мнению В.Л.Макарова, в настоящее время наблюдается взрывообразный процесс появления новых индексов12. И речь здесь идет не о конструировании статистиками и математиками каких-то экзотических формальных показателей, а об отражении новых явлений в относительно простых статистических индексах на основе более полного и глубокого понимания социально-экономических процессов. К числу таких индексов можно отнести показатель гарантированного обменного курса (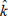 ) С.В.Дубовского, который выглядит следующим образом13:
) С.В.Дубовского, который выглядит следующим образом13: 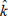 (t) = G(t) / R(t)
(t) = G(t) / R(t)
Данный подход базируется на идее, что рублевые средства, вложенные в ГКО-ОФЗ, по своей сути являются типичными «быстрыми деньгами», которые в любой момент (с учетом сроков погашения) могут перекочевать на валютный рынок. Курс, балансирующий рублевые авуары инвесторов и золотовалютные резервы ЦБ, и является гарантированный валютным курсом С.В.Дубовского. Таким образом, при таком подходе обеспечивается «сцепление» рынка облигаций и валютного рынка, что отсутствует в модели Лукашина-Лушина. По сути дела подобное сцепление двух сегментов финансового рынка означает внесение в анализ фактора неравновесия. Действительно, возможное перетекание средств с рынка облигаций на валютный рынок нарушает имевшееся на нем равновесие и стимулирует установление обменного курса на новом равновесном уровне. Следовательно, здесь речь идет о своеобразном «разрыве» биржевого валютного равновесия.
Проведенные эмпирические расчеты показали, что еще в 1996 г. в России номинальный и гарантированный валютные курсы «рубль/доллар» были близки. Однако уже в начале 1998 г. гарантированный курс вышел на уровень 25 рубль/доллар. Именно до этого уровня и дошла девальвация рубля после августовского валютного кризиса 1998г. Таким образом, гарантированный обменный курс С.В.Дубовского продемонстрировал хорошие диагностические качества в отношении импульсной девальвации национальной валюты.
Между тем гарантированный курс С.В.Дубовского также имеет недостатки. Так, для курса «рубль/доллар» его величина будет играть роль своеобразной «линии поддержки», наподобие той, которая используется в техническом анализе. Однако остается открытым вопрос о «линии сопротивления», которая должна присутствовать в силу принципа симметрии и фиксировать тот уровень курса, до которого он может опуститься при неких катастрофических обстоятельствах. В настоящий момент никаких индексов для построения «линии сопротивления», к сожалению, не предложено. Кроме того, курс С.В.Дубовского хорош при возникновении «взрывов» в динамике валютного курса: в этот момент его величина становится близка к фактической величине курса. В остальные периоды времени данный индекс не имеет никакой ценности, т.к. фиксирует гипотетическую «линию поддержки», весьма далекую от реальных значений курса.
Из сказанного следует, что биржевая модель Лукашина-Лушина не может быть использована для экономик со «слившимися» рынком капиталов и валютным рынком. Взаимообусловленность валютной и долговой политики государства практически полностью исключает приложение простых равновесных схем биржевых торгов для прогнозирования динамики валютного курса. Особенно проблематично их применение для стран, испытывающих сложности в обслуживании внутреннего и внешнего долга.
6. Необходимость построения синтетических моделей динамики валютных курсов. Проведенный анализ позволил выявить те проблемы, которые встают при прогнозировании валютных курсов. Мы просмотрели, пожалуй, самые перспективные модели формирования валютных курсов, однако ни одна из них не может применяться в готовом виде. Между тем каждая из этих моделей вскрывает какой-то очень важный момент исследуемого процесса и поэтому не может быть огульно отвергнута.
Довольно любопытной является «история жизни» некоторых рассмотренных моделей. Так, например, модель А.А.Первозванского великолепно воспроизводила начавшийся в России в 90-х годах процесс сближения ППС и валютного курса. Однако она оказалась принципиально неспособной предсказать обвальную девальвацию рубля в 1998 г. Можно сказать, что валютный кризис 1998 г. «отбросил» неравновесную модель А.А.Первозванского в качестве возможного инструментария объяснения и прогнозирования валютного курса в России.
Модель Ю.В.Ермолаевой также испытала на себе проблемы учета кризиса 1998 г. Так, чтобы построить удовлетворительную эконометрическую зависимость курса от соотношения экспорта и импорта авторам пришлось «чистить» ретроспективные ряды путем выкидывания некоторых кризисных точек. Строго говоря, такой подход является некорректным; в этом случае целесообразно было бы введение так называемых фиктивных (логических) переменных. Однако в любом случае ясно, что валютный «взрыв» 1998 г. в модель торгового баланса естественным образом не вписывается.
Другой вывод, который напрашивается из проведенного анализа, состоит в том, что ни одна из моделей не должна рассматриваться в отрыве от других моделей. Пресловутая «полоса В.А.Евсеева» это продемонстрировала в полной мере. Из ее существования, в частности, вытекает, что неравновесная теория ППС и теория торгового баланса внутренне едины и связаны между собой некими граничными условиями.
Модель Лукашина-Лушина даже для «обычных» валютных флуктуаций была не свободна от технических проблем. Например, при оценке параметров авторами проводилась серьезная фильтрация первичных статистических рядов. В частности, торги, на которых курс не менялся, были исключены из рассмотрения. Кроме того, для растущего курса были исключены два наблюдения с резким ростом курса, вызванным биржевой паникой, а для падающего курса были исключены 12 точек, характеризующихся неэластичным предложением и сверхэластичным спросом. Разумеется, при таком ограниченном диапазоне устойчивости модели отловить с ее помощью возможный 4-кратный рост курса в 1998 г. было просто невозможно. С ее помощью произошедший обвал рубля хорошо объясняется, но для точного или даже ориентировочного прогноза глубины этого обвала модель Лукашина-Лушина не годится.
Сказанное подводит к выводу, что прогнозирование валютных курсов должно строиться все-таки не на одной какой-то модели, а на некоем модельном комплексе. Такая идея высказывалась и ранее. Рассмотренные выше результаты исследований последних лет показывают, что довольно перспективным направлением в этой области может стать построение синтетической неравновесной модели ППС.
2. Вызов современной теории: синтетические модели динамики валютных курсов
Бесперспективность применения какой-либо одной модельной схемы для прогнозирования обменного курса осознана давно. Следующим логическим шагом в исследовании динамики курсов, как и следовало ожидать, стало построение синтетических моделей, которые бы включали множество факторов. Однако на практике такой подход принял довольно странные формы. Практически все прикладные модели аналитиков грешат одним недостатком – эклектичностью набора независимых факторов валютного курса. В данной статье мы не ставим задачу сделать полный обзор подобных моделей. Мы ограничимся лишь показом основных недостатков предлагаемых синтетических моделей динамики валютных курсов на примере некоторых из них.
Одной из наиболее «свежих» эконометрических зависимостей в данной области является модель В.С.Панфилова, которая имеет следующий вид14:
Во-первых, сам набор факторов принципиально эклектичен. Так, фигурирующий в ней индекс потребительских цен характерен для теорий и моделей ППС, а показатель золотовалютных резервов ЦБ – либо для теорий платежного баланса, либо для неравновесных концепций биржевых торгов. Такое совмещение столь разноплановых факторов вызывает сомнения. Например, если уж учитывается инфляция, то она должна учитываться в обеих странах (если рассматривается курс «рубль/доллар», то в России и США). Если же говорить о показателе золотовалютных резервов ЦБ, то он должен с чем-то соотноситься: либо с объемом ВВП страны, либо с объемами государственных долговых обязательств (как это делается при оценке гарантированного курса С.В.Дубовского). В любом случае в такой откровенно опримитивленной форме модель В.С.Панфилова, скорее всего, будет генерировать очень грубые прогнозные оценки.
Во-вторых, имеются и чисто эмпирические неувязки подобной схемы. Например, фактор инфляции устойчиво «работает» при формировании валютного курса при рассмотрении длинных динамических рядов с годовой разбивкой, в то время как золотовалютные резервы ЦБ оказывают заметное влияние на коротких кризисных этапах экономического развития страны. Более того, некоторые «пробные» расчеты показали, что даже при исследовании квартальных агрегатов фактор золотовалютных резервов ЦБ не влияет на динамику курса «рубль/доллар»15. И, наконец, сам В.С.Панфилов не привел в своей работе статистические характеристики качества построенной модели, что оставляет вопросы в правомерности ее широкого применения для прогнозных оценок.
Модификацией рассмотренной модели динамики валютного курса является эконометрическая модель Е.Т.Гурвича и А.В.Дворковича16. В ней вместо фактического валютного курса фигурирует его ожидаемая величина, а в качестве объясняющих используются следующие переменные: международные (золотовалютные) резервы, объявленный правительством темп инфляции (вместо фактического в модели В.С.Панфилова) и ожидаемый валютный курс предыдущего периода. И хотя построенная модель обладала весьма хорошими статистическими характеристиками, ей присущи те же недостатки, что и модели В.С.Панфилова. Более того, введение в рассмотрение виртуальных (ожидаемых и официально объявляемых) переменных присуще концепции капитальных активов и теории валютных экспектаций. Между тем данные направления моделирования курса в качестве объясняемой переменной рассматривают реальный (текущий) спот-курс, а в качестве объясняющей – ожидаемый форвардный курс. Модель Гурвича-Дворковича нарушает эту схему и переводит исследование в чисто виртуальную плоскость. Таким образом, в рассмотренной модели теоретическая эклектичность присутствует в еще большей степени, чем в модели В.С.Панфилова. Следовательно, можно утверждать, что модель Гурвича-Дворковича содержит довольно много теоретических шероховатостей, чтобы ее можно было рассматривать как удачный вариант синтетической модели формирования валютного курса.
Таким образом, попытка построить более сильную прикладную модель динамики курса, опираясь на «синтетическую» концепцию, не увенчалась успехом.
Сказанное наводит на мысль, что столь же несостоятельными будут и все другие попытки «усиления» прогнозных эконометрических моделей за счет «игры» с входящими в них факторами. Фактически это означает, что брошенный современной наукой вызов, базирующийся на построении синтетических эконометрических моделей, постепенно затих без видимых достижений. По-видимому, имеет смысл искать какие-то другие пути совершенствования прикладного аппарата прогнозирования валютных курсов. Подобные попытки набирают обороты. Рассмотрим некоторые из них.
Небезынтересной представляется методология логических цепей Дж.Сороса, позволяющая отследить возникновение рефлексивных связей на валютном рынке. Сущность данного подхода заключается в соизмерении «веса» основных групп факторов валютной динамики, в результате чего возникает эффект девальвации или ревальвации национальной валюты. Так, например, в соответствии с традиционной концепцией торгового баланса возрастание его дефицита ведет к девальвации национальной валюты и падению темпов экономического роста. Однако во время правления Р.Рейгана в США ухудшение торгового баланса сопровождалось усилением позиций доллара. Для объяснения подобного феномена Дж.Сорос использовал следующую простую логическую цепочку17:
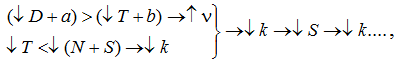
В соответствии с приведенной схемой увеличение бюджетного дефицита «перевесило» негативное влияние уменьшения торгового баланса и тем самым поддержало экономический рост. В это же самое время приток в страну спекулятивного капитала компенсировал долговые платежи и «перекрыл» уменьшение торгового баланса, приведя тем самым к укреплению доллара. В дальнейшем укрепление доллара стимулировало дополнительный приток спекулятивного капитала с последующим витком ревальвации и т.д. Схема «размыкается» и связи меняют направление, если условия в фигурных скобках не выполняются. В этом и состоит, пожалуй, главное достоинство логических цепей Дж.Сороса.
Подобные логические схемы напоминают химические формулы и направлены на определение качественных сдвигов в динамике валютных курсов. На наш взгляд, подобные схемы в будущем могут представлять серьезную альтернативу современным экономико-математическим моделям, также как химические формулы и модели в определенном смысле сейчас противостоят математическим формулам и моделям. Тем не менее, логические цепи в нынешнем виде имеют определенные недостатки.
Во-первых, все переменные схемы должны быть полностью выверены и хорошо верифицированы, чего сейчас не наблюдается. Во-вторых, сама справедливость логических условий должна быть проверена на реальных статистических данных. В-третьих, необходимо определить прочие неучтенные факторы, оценить их количественно и непротиворечивым образом интегрировать их в общую схему. В-четвертых, следует определить временной интервал, на котором действуют рассмотренные логические условия. Пока эти задачи не будут решены, логические цепи Дж.Сороса не смогут стать эффективным рабочим инструментом прогнозирования валютных курсов.
Другим подходом к решению проблемы прогнозирования динамики курсов был высказан Е.В.Балацким18. В соответствии с ним имеет смысл сконцентрировать усилия на механизме «чередования» и взаимоувязки частных моделей динамики курсов. Однако высказанная, на наш взгляд, плодотворная идея не была доведена до конкретной реализации. Видимо, разработка синтетического модельного комплекса с соответствующим алгоритмом его работы и является наиболее перспективным направлением в данной области, вписывающимся в современные инструментальные императивы синтетических моделей.
3. Динамика валютного курса в России с точки зрения теории равновесия
Выше нами было сказано, что неравновесная модель А.А.Первозванского описывает слишком гладкие траектории соотношения «курс/ППС». Вместе с тем эконометрическая зависимость Волконского-Кузовкина позволяет в каком-то смысле уточнить ее путем введения более точного понятия равновесного значения соотношения «курс/ППС» (Ω*), которое рассчитывается по формуле:
В соответствии с полученными оценками, равновесное отношение «курс/ППС», хотя и меняется во времени, но настолько незначительно, что его можно полагать константой:
Дело в том, что в соответствии с логикой А.А.Первозванского отношение Ω, достигнув в 1995 г. своего «дна» (табл.1), должно было и дальше постепенно уменьшаться, стремясь к единице. Однако этого не произошло, и в последующие годы начался подъем величины Ω вплоть до своего «пика» в 1999 г. (1992 год был нерепрезентативным, так как в это время в России только начала формироваться система плавающего валютного курса). После этого снова началось длительное снижение Ω, однако оно оказалось не столь быстрым, как этого можно было ожидать. Подобные «откаты» от предсказанной тенденции стремления к идеальному равновесию Ω=1 легко объясняются путем введения уточненного равновесия
| Годы | Фактическое отношение «курс/ППС» | Равновесное отношение «курс/ППС» |
|---|---|---|
| 1992 | 11,5 | 2,9 |
| 1993 | 3,7 | 2,8 |
| 1994 | 3,1 | 2,7 |
| 1995 | 1,9 | 2,7 |
| 1996 | 2,3 | 2,7 |
| 1997 | 2,3 | 2,8 |
| 1998 | 3,4 | 2,9 |
| 1999 | 5,3 | 3,0 |
| 2000 | 3,8 | 3,0 |
| 2001 | 3,3 | 2,9 |
Зафиксированные статистикой колебания величины Ω относительно своей равновесной точки притяжения
В настоящий момент с учетом «обновленных» представлений о курсообразовании можно предложить трехступенчатую долгосрочную модель динамики валютного курса. Рассмотрим принципы ее построения и основные составляющие.
Во-первых, она должна базироваться на классической схеме «нащупывания» величиной Ω своего равновесия Ω*, т.е. динамика Ω должна определяться ее текущим отклонением от точки Ω*. Только в этом случае мы сможем отобразить в модели выявленный колебательный режим фактической величины Ω относительно своего равновесного состояния Ω*.
Во-вторых, схема «нащупывания» должна включать механизм инерции и запаздывания реакции Ω на возникающее отклонение от равновесия Ω*. Выявленные 2-3-годовые циклы в движении Ω относительно равновесной величины Ω* (табл.1) объективно предполагают наличие временных лагов в выравнивании двух величин.
В-третьих, необходимо использовать скользящее прогнозирование точки равновесия Ω*, т.е. учитывать ее возможные динамические изменения. В условиях резких сдвигов в темпах экономического роста и уровне жизни корректировка точки равновесия становится значимой процедурой прогнозирования.
В-четвертых, помимо модели прогнозирования величины Ω, необходима модель прогнозирования показателя ППС, который учитывает ценовые сдвиги внутри страны и за ее пределами. Корректировка величины ППС становится особенно значимой в периоды высокой инфляции. Здесь же следует сказать, что работа с показателем ППС требует унификации самой методики ее расчета. Дело в том, что сейчас в России существует множество альтернативных оценок ППС «рубль/доллар», которые подчас принципиально различаются. Поэтому унификация методики и информационной базы для расчета ППС является необходимым условием проведения прикладных расчетов динамики величины Ω.
В-пятых, величина валютного курса должна определяться непосредственно на основе прогнозных оценок Ω и ППС. Иными словами, величины Ω и ППС являются вспомогательными для определения собственного валютного курса.
На наш взгляд, учет всех перечисленных моментов позволяет сформировать вполне удовлетворительную модель долгосрочного прогнозирования валютного курса. Рассмотрим ее звенья.
1-ое звено – прогноз отношения Ω. Для прогнозирования данной относительной величины сначала необходимо установить ретроспективную закономерность ее движения во времени. На наш взгляд, это можно сделать с помощью эконометрической модели следующего вида:
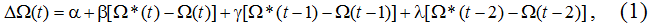
В соответствии с моделью (1) величина изменения Ω определяется текущим расхождением с точкой равновесия и расхождением, имевшим место в прошлый и позапрошлый периоды (годы). При необходимости модель (1) можно уточнить путем введения нелинейных элементов. Таким образом, зависимостью (1) моделируется распределенный эффект влияния неравновесных «зазоров» на будущую динамику этих «зазоров». Фактически мы здесь имеем адаптивный механизм нащупывания равновесия, который и генерирует колебательный режим.
На основе расчетов по модели (1) можно перейти непосредственно к прогнозной величине Ω с учетом прогнозируемой величины точки равновесия

Заметим, что модель (1) является ядром предлагаемой синтетической модели. Это связано с тем, что именно величина Ω имеет определенные закономерности формирования в динамике и именно за этот факт и следует «зацепиться» при осуществлении прикладных прогнозов.
2-ое звено – прогноз ППС Θ(t+1). Для прогнозирования данной величины необходимо иметь прогнозы инфляции в двух рассматриваемых странах, а также возможные сдвиги в товарных наборах, которые используются для вычисления ППС.
3-ое звено – прогноз валютного курса k(t+1). Для прогнозирования курса достаточно воспользоваться данными предыдущих двух этапов и тождественным соотношением:

Философия предложенного подхода проявляется именно на третьей стадии при осуществлении процедуры (3). Дело в том, что, как показывало наше исследование, никаких надежных методов прогнозирования такой неустойчивой величины как валютный курс не существует. Зато можно более или менее уверенно прогнозировать относительно устойчивую величину Ω. Именно поэтому мы и идем в таком направлении, что сначала осуществляем прогноз более стабильной величины Ω, а уже потом на нее «навешиваем» прогнозную величину ППС и на этой основе определяем искомую величину валютного курса.
Эмпирическая проверка теоретической модели (1) позволила получить следующую эконометрическую зависимость:
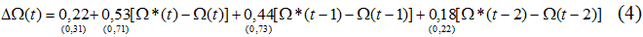
В скобках под коэффициентами регрессии указаны значения их t-статистик; под уравнениями регрессии приведены коэффициент детерминации и число статистических наблюдений.
Как показывают расчеты, F-статистика модели (4) равна F=0,89, что намного превышает ее критическое значение в 0,51. Таким образом, построенная регрессионная зависимость (4) проходит основной статистический тест и может быть признана удовлетворительной.
Так как длина циклических колебаний в исходной траектории фактического значения «курс/ППС» относительно точки равновесия почти все время равна трем годам, то и регрессия (4) предполагает глубину временного лага в два года.
В целом модель (4) можно считать весьма удачной. Помимо удовлетворительных статистических характеристик этому факту содействуют еще два момента. Во-первых, зависимость (4) совершенно верно отражает направление изменений фактической величины. Во-вторых, рассмотрение структуры коэффициентов модели (4) свидетельствует о выполнении классической гипотезы распределенных моделей, а именно: значение коэффициентов модели уменьшается по мере возрастания глубины запаздывания. Это означает, что для рассматриваемой системы неравновесные «зазоры», более отдаленные во времени, играют меньшую роль при формировании текущего курса, нежели «зазоры», более близко примыкающие к текущему моменту. Иными словами, память системы обладает своеобразным свойством постепенного «забывания» происходящих событий.
Выше мы предложили общие контуры синтетической неравновесной модели ППС. Настаивать на окончательном виде модели (4) было бы неверно, так как эмпирическая проверка ее затруднительна из-за плохого информационного обеспечения. Во-первых, пока имеются очень ненадежные данные как о фактических, так и о равновесных значениях показателя Ω. Во-вторых, пока мы имеем короткие динамические ряды. Учитывая, что модель (4) предусматривает временные запаздывания глубиной в 2 года, на сегодняшний день мы имеем всего лишь 8 отчетных точек, которые могут использоваться при построении эконометрической зависимости. Этого явно недостаточно для установления высоконадежной связи. Однако через 3-4 года уже можно будет проводить более серьезные «пробы» трехступенчатой схемы.
Предложенная схема имеет ряд плюсов по сравнению со многими рассмотренными выше подходами. Во-первых, она чрезвычайно проста в вычислительном плане. Одна простая регрессионная модель, одна экстраполяционная формула и два тождества исчерпывают весь вычислительный арсенал предложенной схемы. Во-вторых, она очень проста в плане интерпретации, так как не «утяжелена» многочисленными объясняющими факторами. Все движения курса объясняются существующей инерционностью системы в подстраивании под равновесное состояние. В-третьих, она позволяет надеяться на более стабильный результат, так как она основана не на факторной закономерности формирования валютного курса, а на временной закономерности. Иными словами, вместо многочисленных сложных факторов, живущих своей собственной «жизнью», мы имеем только один фактор – время. И этот фактор уже «вложен» в структуру модели и его самостоятельный прогноз не требуется.
Разумеется, дальнейшие экспериментальные расчеты могут несколько скорректировать формулу (4). Однако даже это не меняет логики предложенной схемы. Более того, при проведении скользящих прогнозных расчетов модель (4) должна постоянно корректироваться, за счет чего будет происходить ее своевременная адаптация к возможным изменениям самого механизма настройки системы на свое равновесное состояние.
Предложенная модель позволяет сформировать долгосрочную прогнозную траекторию валютного курса. Подобный прогноз может использоваться государственными органами исполнительной власти в качестве элемента более масштабных правительственных прогнозов экономического развития страны, а также крупными коммерческими структурами для оптимизации своих долгосрочных производственных и торговых программ.



































Написать комментарий