Расчет эффективности инвестиций в образование с учетом их кредитного характера

Стоит ли брать кредит под образование? Является ли высшее образование рентабельным проектом, в который стоит вкладывать заемные средства? Как рассчитать эффективность таких вложений? Каковы количественные оценки подобного рода инвестирования?
Становление в России рыночных отношений предполагает формирование рынка человеческого капитала. В свою очередь наличие последнего невозможно без развитого рынка инвестиций в человеческий капитал, который состоит, по крайней мере, из двух сегментов: собственных и заемных средств хозяйственных субъектов, использующихся ими в качестве инвестиций для получения общего и специального образования. На каждом из указанных двух сегментов рынка инвестиций в образование действуют свои закономерности, которые до сих пор не нашли должного отражения в специальной литературе. Между тем актуальность данной проблемы становится все более очевидной в силу продолжающегося расширения сферы платного образования. Одновременно с этим обучение на коммерческой основе в значительной мере сдерживается недостаточно высокими доходами населения, а, следовательно, и его низкой инвестиционной активностью.
На наш взгляд, серьезным резервом в расширении рынка инвестиций в человеческий капитал являются кредитные ресурсы коммерческих банков и инвестиционных фондов. Однако данные структуры пока никак не подключены к данному процессу. Что же мешает активному задействованию кредитного фактора? Какие необходимы изменения для улучшения ситуации на таком важном рынке, как рынок инвестиций в высшее и послевузовское образование? Попытаемся разобраться в данных вопросах путем уяснения существующих в данной области количественных связей.
1. Рентабельность вложений в образование с учетом их кредитного характера; основные соотношения
В более ранних работах, посвященных инвестициям в человеческий капитал, была разработана методика оценки рентабельности собственных средств частных лиц, используемых в качестве инвестиций в знания [1]. Однако использование кредитных средств на образовательные нужды индивидуумов предполагает существенную модификацию данной методики. Это связано с тем, что сам процесс использования экономическими агентами кредитов на «покупку» образования кардинально отличается от аналогичного процесса с использованием ими собственных финансовых ресурсов. Какими формулами можно воспользоваться, чтобы оценить рентабельность кредитных вложений в образование?
Как и в случае собственных средств, рентабельность (r) кредитных вложений в образование следует рассчитывать по следующей формуле [1]:

В соответствии с соотношением (1) рентабельность вложений в получение образования отождествляется с нормой прибыли данной операции, предполагающей полные затраты на образование R, доход (выигрыш) от его получения π и период (год) выхода индивида на пенсию Θ. Это означает, что за время Θ хозяйственный субъект получает образование и путем его эксплуатации «оборачивает» изначальные издержки R, получая суммарный денежный эффект π. Таким образом, величина r представляет собой доход на каждый рубль, вложенный в получение образования.
Раскроем компоненты формулы (1). Для этого прежде всего оценим полные затраты человека в образование. Они складываются из денежных затрат на образование в виде платы за учебу G и упущенных заработков W. В соответствии с современными представлениями помимо прямых издержек G на получение знаний учитываются еще и альтернативные издержки W, связанные с затратами времени на обучение T, которое могло бы быть использовано для зарабатывания денег [2, с.112]. Таким образом, «потерянные заработки», то есть доход, недополученный учащимися за годы учебы, входит в состав издержек обучения в качестве главного элемента. По существу, потерянные заработки измеряют ценность времени учащихся, затраченного на формирование их человеческого капитала [3, с.21]. В соответствии с таким подходом рыночная цена учебы суммируется с упущенными заработками, которые вычисляются в виде произведения времени учебы и ставки заработной платы, по которой мог бы реально оплачиваться труд учащегося. Такие полные затраты, осуществляемые в каждом году, должны дисконтироваться на протяжении всего периода учебы в соответствии с минимальной процентной ставкой.
Обоснованием подобной процедуры дисконтирования служит тот простой факт, что данная сумма могла быть вложена, например, на депозитный вклад в банк или в государственные ценные бумаги, которые ежегодно приносили бы определенный процент. Получившаяся таким образом сумма должна дисконтироваться на протяжении периода времени, следующего сразу после завершения учебы и заканчивающегося в момент выхода человека на пенсию. Итоговая формула для оценки полных приведенных затрат на образование R для случая собственных средств может быть записана следующим образом:
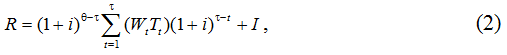
Формула для оценки полных приведенных затрат на образование R для случая заемных средств может быть записана аналогичным образом:

Для оценки совокупного дохода π, получаемого от инвестиций в образование, необходимо сопоставить доходы Wt, которые человек мог бы получать в течение жизни после окончания срока учебы, не имея образования, с доходами Dt, который он будет получать, имея образование. Разница между этими величинами должна дисконтироваться на протяжении всего периода времени от момента завершения учебы до момента выхода на пенсию. Учитывая сказанное, полный приведенный доход от образования π для случая кредитных средств может оцениваться точно также, как и для случая собственных средств [1]:

Имея соотношения (2)-(4), можно для каждого конкретного случая легко рассчитать по формуле (1) рентабельность вложений в образование.
Так как первый компонент правой части в формулах (2) и (3) совпадает, то особого комментария заслуживают лишь показатели I и K, которые, собственно говоря, и несут в себе принципиальное различие, заложенное в функционировании рынков собственных и заемных средств.
Если индивидуум вносит плату за предоставляемое ему образование всю сразу, т.е. до начала учебы, то в этом случае величина I может оцениваться по простейшей формуле:

Если же инвестор не сразу вносит всю плату за образование, а равномерными порциями по годам, то расчетная формула примет следующий вид:

Перейдя в формуле (6) от дискретных величин к непрерывным, зависимость (6) можно переписать в более функциональной форме1:

Формулы (5) и (6) воспроизводят ситуацию, когда цена образования выплачивается человеком за счет его собственных средств. Грубо говоря, эти средства он достает из кармана и отдает за свое обучение, вместо того, чтобы положить их на депозитный счет в банке и до конца жизни получать с них проценты. Безусловно, такая альтернатива увеличивает итоговую цену образования, что и учитывается формулами (5) и (6).
Если же плата за образование вносится хозяйственным субъектом за счет кредитных средств, то формулы (5)-(7) перепишутся в следующем виде:



В отличие от случая (8), когда индивидуум берет в банке сразу всю сумму для оплаты своего обучения, формула (10) отображает ситуацию, когда кредит берется равномерными порциями каждый год, а накопленная за годы учебы общая сумма кредита погашается единовременно, т.е. вся сразу. Чтобы не усложнять расчетно-аналитическую схему мы в дальнейшем не будем учитывать случай поэтапного, «порционного» погашения кредита. Обобщение на данный случай довольно очевидно, однако весьма громоздко и не несет содержательных методических новаций.
Записанные в данном разделе статьи соотношения позволяют оценить уровень рентабельности кредитных вложений в образование. Как видно из формул (5)-(10), в общем случае отдача от собственных и заемных средств различна, чем и обусловлена необходимость корректировки соответствующего методического инструментария.
2. Временная структура процесса инвестирования в образование с использованием кредитных средств
В нашем анализе фигурируют три основные временные характеристики: τ – период учебы, m – время возврата кредита и Θ – время выхода индивидуума на пенсию. Данные величины являются главными слагаемыми жизненного цикла человека. Однако определенного комментария заслуживает способ их учета. Дело в том, что нулевой период в нашей схеме сопряжен в моментом начала учебы и дальнейший отсчет времени идет именно от этой точки. Срок погашения кредита составляет величину, которая складывается из периода учебы τ и послеучебного периода m–τ, в течение которого человек «отрабатывает» полученный заем. Временной интервал от начала учебы до момента выхода индивида на пенсию Θ представляет собой инвестиционный (можно сказать, учебно-производственный) цикл, в рамках которого протекает вся его активная деятельность. Соответственно, период Θ–τ предназначается для эксплуатации полученных навыков и знаний и именно на этом отрезке жизненного пути человека происходит формирование нормы прибыли от вложений в образование.
Помимо указанных временных характеристик в состав жизненного цикла человека входят еще две временные «полосы»: h – период до начала учебы и n – пенсионный период. В нашей схеме рождение индивида происходит в точке –h, а момент его смерти приходится на момент времени Θ+n. Сумма h+Θ+n и составляет жизненный цикл человека. Общая схема жизненного цикла экономического агента и его составляющих приведена на рис.1.
«Вырезание» из нашего анализа временных отрезков h и n связано с тем, что они, вообще говоря, не влияют на эффективность инвестиций в образование. Можно сказать, что изменение длины h автоматически сказывается на величине Θ, поэтому базовые временные характеристики имеет смысл «очистить» от избыточных факторов. Однако определенный вопрос остается в отношении пенсионного периода. Так, в соответствии с нашей методикой приведение всех финансовых показателей к единой базе происходит до момента выхода человека на пенсию. Тем самым нами предполагается, что после завершения трудовой деятельности индивид «теряет» все инвестиционные эффекты. В общем случае это не совсем так. Действительно, сэкономленные на учебе деньги, также как и чистый доход от полученного образования расходуются не сразу после выхода на пенсию, а постепенно. Это означает, что проценты на данные суммы будут еще некоторое время «накручиваться»: либо вплоть до смерти человека, либо до момента полной растраты накопленной суммы. Однако данный аспект инвестирования средств в образование, во-первых, является не слишком важным, а, во-вторых, предполагает много методических нюансов, учет которых не оправдывает себя. Поэтому мы в данном случае следуем традиционному подходу, который игнорирует пенсионный период жизненного цикла инвестора.
3. Особенности инвестирования в образование на рынках собственных и заемных средств.
Из формул (8)-(10) хорошо видна принципиальная разница между случаями собственных и заемных средств. Так, в случае заемных средств суммарная цена образования увеличивается за счет начисляющихся процентов за кредит до момента его полного погашения. В случае собственных средств суммарная цена образования увеличивается за счет упущенных депозитных процентов, начисляющихся в течение всего жизненного цикла индивида. При этом ясно, что процент за кредит больше процента по депозиту и, следовательно, «процентная» составляющая на рынке собственных средств оказывает менее болезненное воздействие на рентабельность инвестиционной операции, чем на рынке заемных средств. С другой стороны, период погашения кредита значительно короче жизненного цикла работника, что дает определенное преимущество рынку заемных средств по части «временной» составляющей. Таким образом, сказать заранее о том, какими средствами выгоднее воспользоваться (собственными или заемными) при осуществлении инвестиций в образование нельзя.
Заметим по ходу дела, что цена образования для заемных средств является совершенно реальной, т.к. проценты за кредит представляют собой фактическую надбавку к его исходной сумме. Наоборот, цена образования для собственных средств в значительной мере является фиктивной, ибо она учитывает возможный эффект от вложения денег в альтернативные инвестиционные проекты. Это означает, что при слабом и ненадежном банковском секторе, а также в условиях политической нестабильности роль дисконт-фактора i становится все менее заметной и, следовательно, все слабее проявляется «полная» цена образования для случая собственных средств хозяйственных участников.
В простейшем случае, описывающемся формулами (5) и (8), условие равной выгодности в осуществлении инвестиций в образование на базе собственных и заемных средств получается из равенства правых частей (5) и (8) и выглядит следующим образом:

Данное соотношение можно переписать в виде более простого и наглядного условия равновесия2:

Если условие (12) нарушается и записанное уравнение не выполняется, то возникает ситуация «перевеса» одного из анализируемых инвестиционных рынков. Так, при mq>iΘ более выгодно вкладывать в образование собственные денежные средства, а при mq<iΘ имеет смысл воспользоваться кредитом. Данная дихотомия достаточно важна и интересна. Из нее, в частности, следует, что в экономике могут возникать такие условия, при которых выгоднее быть «бедным» инвестором и взять для получения образования кредит, нежели быть «богатым» и вложить собственные финансовые ресурсы с заведомо более низкой отдачей.
Данный вывод противоречит обыденной логике и расхожему мнению, что свои средства всегда лучше, чем заемные. Действительно, на бытовом уровне кредитные деньги всегда «дороже» собственных. Однако в более сложном случае фактор дисконтирования, как было показано выше, опрокидывает данные примитивные рассуждения и приводит к прямо противоположному выводу. Характерно, что без учета фактора дисконтирования по депозитному проценту i условие равновесия (12) вырождается в тривиальное неравенство mq>0. Содержательно это означает, что использование заемных средств для осуществления инвестиций в образование всегда менее рентабельно, чем использование собственных. Таким образом, игнорирование депозитного дисконт-фактора при калькуляции полных затрат на получение образования может приводить к потере важных закономерностей функционирования рынка инвестиций.
Кроме того, на примере условия (12) мы фактически можем визуально наблюдать возможности государства по формированию определенного инвестиционного климата на рынке образования. Так, если в обществе «накопилось» много малообеспеченных людей, как, например, в современной России, то государство, правильно манипулируя процентными ставками, может поддержать спрос на рынке кредитов и тем самым обеспечить широким массам доступ к образованию. Разумеется, все сказанное справедливо для экономики с развитым механизмом процентных ставок, где не только государство, но и сами хозяйственные субъекты чутко реагируют на любые сдвиги в их величине.
Если ввести в рассмотрение понятие процентной маржи как разницы между кредитным и депозитным процентами


Если фактическая маржа меньше правой части (13) и (14), то для экономического агента целесообразно использовать заемные средства. Таким образом, для стимулирования спроса на кредит под образовательные услуги государство должно ограничивать прибыльность кредитных операций банков и финансовых компаний либо путем установления потолка для процента за кредит, либо путем лимитирования максимальной величины процентной маржи. В этой связи, несмотря на эквивалентность соотношений (13) и (14), более предпочтительной для практического использования следует признать формулу (13).
4. Ограничители потенциальных возможностей кредитного рынка; условие возврата заемных средств
Записанные выше соотношения позволяют без особых сложностей проводить расчеты рентабельности инвестиций в образование, осуществляемых на кредитной основе. Однако в общем случае практически все величины, фигурирующие в нашей схеме, являются нестационарными. Это означает, что на практике мы вынуждены работать с временными траекториями соответствующих показателей, а это уже само по себе отрицает возможность построения простых аналитических конструкций, которые могли бы использоваться как для лучшего понимания характера протекающих в обществе процессов, так и для ориентировочных прикладных расчетов. В связи с этим, сознательно идя на явное упрощение реальности, предположим неизменность во времени основных переменных нашей модели:
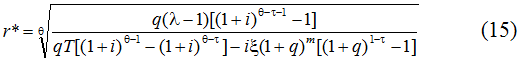
Однако вычисление уровня рентабельности по формуле (15), вообще говоря, недостаточно для полного понимания ситуации в сфере кредитования в образования. Дело в том, что между инвестициями на базе собственных и заемных средств имеется принципиальная разница. Так, при вложении собственных средств индивидуум должен учитывать только величину рентабельности таких инвестиций. Если же он использует заемные средства, то такого учета совершенно недостаточно. Помимо этого он вынужден оценивать возможности своих будущих заработков для своевременного покрытия взятого кредита. На практике может оказаться, что предполагаемый разрыв в оплате труда субъекта после учебы обеспечивает вполне удовлетворительную рентабельность вложений в образование, но не позволяет покрыть кредитные обязательства в нужный срок. В этом случае решение о взятии кредита на получение образования отклоняется. Аналогичная оценочная процедура проводится и самим кредитором, что позволяет ему застраховать себя от слишком рискованных операций.
Таким образом, помимо «итоговой» оценки эффективности заемных инвестиций в образование (15), экономический агент должен еще проводить «промежуточное» тестирование инвестиционной операции с точки зрения его возможностей расплатиться за взятый кредит. Условие погашения кредита в общем случае можно записать следующим образом:

В основе формулы (16) лежит представление о том, что кредит гасится через m лет после взятия его первой порции, причем погашение производится полностью, а не по частям. Одновременно с этим мы предполагаем, что первые годы после окончания учебы заемщик живет чрезвычайно скромно, довольствуясь минимумом; остальные деньги он копит для погашения кредита. Процесс накопления ускоряется за счет депозитного дисконта i. Как в теории, так и на практике в качестве величины M может использоваться не только прожиточный минимум, но и вообще любая величина, обеспечивающая накопление необходимой суммы для возврата долга; прожиточный минимум нами используется для большей конкретизации и наглядности проводимых в дальнейшем расчетов.
После введения в рассмотрение коэффициента
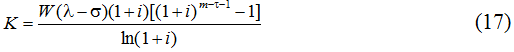
Для того, чтобы выписать окончательное условие возврата кредита следует приравнять правые части формул (10) и (17). В результате простейших преобразований получим следующее уравнение:
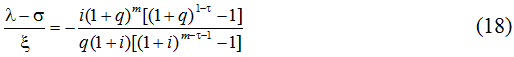
Формула (18) позволяет оценить минимальный разрыв в заработной плате индивидуума λ до и после получения образования. Если ожидаемая фактическая величина не дотягивает до ее критического значения, то кредитная сделка не состоится. Таким образом, оценка рентабельности инвестиций в образование предваряется проверкой условия (18). В этом состоит главное отличие процесса инвестирования на основе заемных средств по сравнению с использованием собственных финансовых ресурсов.
5. Учет динамики доходов инвестора в расчетах рентабельности вложений в образование
Выше нами были получены формулы в предположении постоянства доходов индивидуума как до, так и после получения образования. При этом нас особенно интересовал вопрос об эффективной величине разрыва в возможных заработках. Разумеется, на практике доходы человека меняются на протяжении жизненного цикла, причем динамика таких изменений, как правило, имеет ярко выраженный повышательный тренд. Учет данного факта предполагает определенную модификацию нашей модельной схемы.
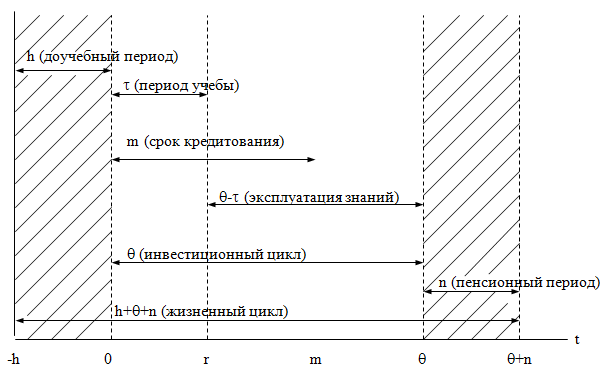
Рис.1. Временная структура процесса инвестирования в образование как часть жизненного цикла индивидуума.
Динамизация доходов предполагает довольно интересные моменты как в формальном, так и в содержательном плане. Например, в простейшем случае временная разверстка процесса изменения доходов может быть представлена на рис.2, где заработки инвестора после получения образования сразу становятся выше, чем без него (суммарный выигрыш представлен площадью заштрихованной фигуры). Значительно более интересным представляется случай, когда экономический агент после завершения учебы «садится» на зарплату ниже той, которую он мог бы получать, не имея образования. Однако в дальнейшем его заработки начинают расти быстрее, чем у «необразованного» субъекта и на определенном этапе (в точке t*) происходит окончательный перелом в его пользу (см. рис.3, где проигрыш на первом этапе эксплуатации знаний представлен фигурой с левосторонней штриховкой, а выигрыш на втором этапе – фигурой с правосторонней штриховкой). Безусловно, на практике возможны и более сложные временные траектории доходов с многократными точками перелома.
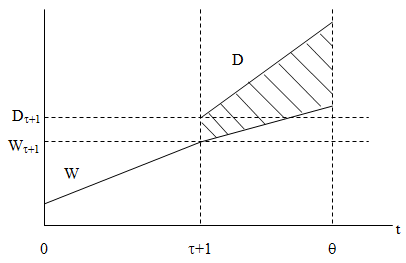
Рис.2. Временная структура динамики доходов индивидуума (случай линейного роста доходов).
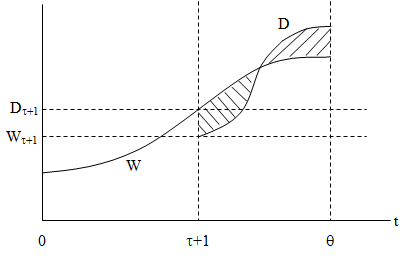
Рис.3. Временная структура динамики доходов индивидуума (случай логистического роста доходов).
Моделирование динамического случая предполагает использование различных гипотез в отношении характера роста доходов. Наиболее типичными являются случаи линейного, экспоненциального и логистического роста. Первый случай предполагает равномерный во времени рост доходов индивида (данный тип роста показан на рис.2), второй – рост с постоянным темпом прироста (для этого случая получены аналитические формулы в [1]), третий – быстрый рост с постепенным замедлением и стабилизацией около точки насыщения к концу трудового стажа (логистические кривые доходов представлены на рис.3). Для каждого из этих случаев можно вывести соответствующие зависимости, однако таковые будут довольно громоздкими и мы их здесь приводить не будем. Важно, пожалуй, лишь то, что во всех этих случаях показатель относительного разрыва в заработках индивида λ в явной форме исчезает. Для его расчета следует воспользоваться соответствующей динамизированной формулой, учитывающей кумулятивные доходы, т.е. доходы, полученные в течение всего цикла эксплуатации знаний:

Возьмем для примера случай экспоненциального роста доходов, где β – темп прироста возможных заработков «необразованного» субъекта Ht в послеучебный период; γ – темп прироста заработков «образованного» субъекта Dt после учебы. Тогда


Формула (21) позволяет задавать в расчетах такие темпы прироста заработков, которые обеспечат надлежащий уровень разрыва в их суммарных величинах λ и в начальный момент времени работы сразу после завершения учебы λ0.
6. Рынок инвестиций в образование: простейшие количественные закономерности
Прежде чем перейти к расчету более тонких эффектов на рынке образования остановимся на самых общих закономерностях. Для этого рассмотрим основополагающее уравнение (12) с точки зрения того, насколько реалистично его выполнение.
Надо сказать, что в реальности вариации процентных ставок по кредитам и депозитам довольно существенны. Причем в зависимости от рассматриваемой страны весьма сильно могут различаться как сами номинальные ставки (в основном из-за различных темпов инфляции), так и их процентная маржа. Так, в 1997 г. разница между ставками по кредитам и депозитам в Японии составляла немного больше 2%, в США – 3%, в Мексике – 10%, а в России – почти 30% [4, с.604]. Иногда наблюдаются еще более экзотические ситуации (как это, например, было в Польше в 1994 г.), когда данный показатель принимает и вовсе отрицательное значение (–0,6% годовых) [4, с.604]. Чтобы не увязнуть в малозначащих различиях сформируем 12 расчетных сценариев, в которых процентные ставки будут принимать некие усредненные величины.
Учитывая, что в уравнении (12) могут меняться не только процентные ставки, но и временные интервалы m и Θ, будем рассматривать три вида инвестиций в образование: на получение высшего образования (учеба в высшем учебном заведении), на получение ученой степени кандидата наук (учеба в аспирантуре) и на получение ученой степени доктора наук (учеба в докторантуре). В рамках каждой разновидности образования будем «обыгрывать» четыре сценария с меняющимися параметрами (табл.1).
| Сценарий расчета | Исходные параметры | Характер неравенства qm∼iΘ |
Выгоден или невыгоден кредит в образование | |||
|---|---|---|---|---|---|---|
| m, год | Θ, год | q, % | i, % | |||
| Высшее образование №1 |
10,0 | 43,0 | 13,0 | 3,0 | 1,30>1,29 | Не выгоден |
| №2 | 10,0 | 43,0 | 12,0 | 3,0 | 1,20<1,29 | Выгоден |
| №3 | 15,0 | 43,0 | 8,0 | 3,0 | 1,20<1,29 | Выгоден |
| №4 | 10,0 | 38,0 | 11,0 | 3,0 | 1,10<1,14 | Выгоден |
| Аспирантура №5 |
8,0 | 35,0 | 13,0 | 3,0 | 1,04<1,05 | Выгоден |
| №6 | 8,0 | 35,0 | 14,0 | 3,0 | 1,12>1,05 | Не выгоден |
| №7 | 10,0 | 35,0 | 10,0 | 3,0 | 1,00<1,05 | Выгоден |
| №8 | 10,0 | 35,0 | 11,0 | 3,0 | 1,10>1,05 | Не выгоден |
| Докторантура №9 |
7,0 | 30,0 | 12,0 | 3,0 | 0,84<0,90 | Выгоден |
| №10 | 7,0 | 30,0 | 13,0 | 3,0 | 0,91>0,90 | Не выгоден |
| №11 | 7,0 | 25,0 | 10,0 | 3,0 | 0,70<0,75 | Выгоден |
| №12 | 7,0 | 30,0 | 10,0 | 2,0 | 0,70>0,60 | Не выгоден |
Проведенные расчеты служат хорошей иллюстрацией по крайней мере двух тезисов. Первый из них носит «негативный» оттенок и его можно сформулировать так: ни один из уровней образования (высшее образование, аспирантура, докторантура) не предполагает явного доминирования какого-либо из двух видов инвестиционных средств (собственных или заемных). Игра экономических параметров может привести к «победе» или «поражению» кредитных средств на любом образовательном уровне. Причем такие сдвиги в значениях параметров находятся в рамках реально возможного хода событий. Придать сформулированному выводу «позитивный» характер с соответствующим выявлением закономерностей для каждого образовательного уровня можно только для экономики с очень стабильными параметрическими конфигурациями.
Второй тезис связан с чрезвычайной неустойчивостью равновесия на рынке инвестиций в образование. Малейшее изменение одного из четырех параметров уравнения (12) может привести к принципиальному пересмотру инвесторами своих решений. Так, например, если в сценарии №1 использование кредитных средств для получения высшего образования невыгодно, то в сценарии №2 уступка кредитором 1% в величине назначаемого им процента за кредит приводит к тому, что использование заемных ресурсов становится заметно выгодней по сравнению с собственными. Таким образом, в любой экономике с развитыми механизмом процентных ставок грань между выгодностью и невыгодностью использования собственных (кредитных) средств всегда будет чрезвычайно зыбкой.
7. Результаты прогнозно-аналитических расчетов
Для уяснения основных рыночных закономерностей в сфере инвестирования в образование проведем некоторые ориентировочные расчеты. Для этого воспользуемся соотношениями (18) и (15). При этом будем придерживаться следующего простого алгоритма анализа. Сначала проверим, насколько сильно ограничивают кредитные условия нижнюю планку заработной платы субъекта после завершения учебы. Это делается путем вычисления соответствующего значения λMIN с помощью уравнения (18). Затем посмотрим, какую рентабельность обеспечивает рост зарплаты λMIN. Если значение рентабельности окажется неудовлетворительным, то оценим необходимую величину разрыва в заработках λ до и после окончания учебы для обеспечения более приемлемой величины отдачи от инвестиций.
Чтобы легче было понять количественные закономерности, действующие на рынке инвестиций в образование, воспользуемся рассмотрением восьми сценариев, которые, несмотря на их некоторую условность, довольно полно раскрывают диапазон возможных ситуаций в реальной жизни. Исходные параметры, характеризующие данные сценарии, приведены в табл.2-3. В табл.4 указаны дополнительные параметры, необходимые для оценки уровня рентабельности инвестиций, и результаты проведенных расчетов по формулам (15) и (18).
| Сценарий | W, долл./мес. | М, долл./мес. | G, долл./год | ξ, % | σ, % |
|---|---|---|---|---|---|
| №1 | 300 | 100 | 1000 | 27,8 | 33,3 |
| №2 | 300 | 200 | 1000 | 27,8 | 66,6 |
| №3 | 300 | 200 | 1000 | 27,8 | 66,6 |
| №4 | 300 | 200 | 1000 | 27,8 | 66,6 |
| №5 | 300 | 200 | 2500 | 69,4 | 66,6 |
| №6 | 300 | 200 | 1000 | 27,8 | 66,6 |
| №7 | 300 | 200 | 2500 | 69,4 | 66,6 |
| №8 | 300 | 200 | 2500 | 69,4 | 66,6 |
| Сценарий | i, % | q, % | m, годы | τ, годы |
|---|---|---|---|---|
| №1 | 3 | 5 | 10 | 5 |
| №2 | 3 | 5 | 10 | 5 |
| №3 | 3 | 8 | 10 | 5 |
| №4 | 3 | 8 | 8 | 5 |
| №5 | 3 | 8 | 8 | 5 |
| №6 | 3 | 8 | 8 | 4 |
| №7 | 3 | 8 | 8 | 3 |
| №8 | 4 | 8 | 8 | 3 |
| Сценарий | Θ, годы | Т, % | λ, число раз | D, долл./мес. | r, % |
|---|---|---|---|---|---|
| №1 | 43 | 100 | 0,70 | 210 | –200,5 |
| №2 | 43 | 100 | 1,01 | 311 | –4,1 |
| №3 | 43 | 100 | 1,13 | 338 | –1,8 |
| №4 | 43 | 100 | 1,48 | 444 | +1,4 |
| №5 | 43 | 100 | 2,70 | 810 | +3,6 |
| №6 | 38 | 100 | 1,08 | 324 | –2,5 |
| №7 | 38 | 100 | 1,20 | 359 | –0,1 |
| №8 | 30 | 100 | 1,18 | 355 | –0,8 |
Какие же выводы можно сделать на основе анализа данных табл.4?
Во-первых, сдвиги в величине таких параметров, как σ и ξ в значительно большей мере влияют на формирование величины разрыва в заработках λ, нежели уровня рентабельности r. Изменения остальных параметров довольно сильно сказываются на обеих выходных переменных λ и r. Содержательно это означает, что цена обучения и уровень прожиточного минимума имеют большое значение, прежде всего, в краткосрочном плане, когда решается вопрос о возможности инвестора расплатиться за взятый им кредит. Изменение же процентных ставок i и q, а также длительности горизонтов «работы» инвестиций τ и Θ, имеют важное значение при формировании долгосрочной инвестиционной стратегии, когда инвестор прикидывает уровень возможной отдачи от производимых им вложений в образование.
Во-вторых, следует признать, что в общем случае условие возврата кредита (18) не является серьезным фактором, сдерживающим использование кредитных средств в качестве инвестиций в образование. В частности, среди рассмотренных нами восьми сценариев только в двух из них (в пятом и шестом) формируется такая величина разрыва в заработках λ, которая предполагает положительную, хотя и не очень высокую, отдачу от инвестиций в образование (см. табл.4). В остальных шести случаях инвестор, даже будучи в состоянии расплатиться с кредитом, все же не возьмет его, так как его рентабельность будет неудовлетворительной. Надо сказать, что практически все цифры минимального разрыва в заработках до и после получения образования являются весьма скромными. Так, например, чтобы в пятом сценарии инвестиции стали высокорентабельными и достигли отметки в 7,1% разрыв в зарплате должен подняться от минимального в 2,7 раза до 8 раз. Соответственно в восьмом сценарии выход на уровень отдачи в 7,4% возможен при обеспечении относительного разрыва в заработках в 3 раза. Таким образом, основные требования к уровню доходов индивида после обучения идут все же со стороны ожидаемой им рентабельности инвестиций, а не со стороны кредитора.
В-третьих, окупаемость инвестиций осуществляется гораздо легче для более поздних этапов обучения. Из приведенных выше данных видно, что в восьмом сценарии достичь высокой окупаемости оказывается гораздо легче, чем в пятом сценарии. При этом стоимость обучения в восьмом сценарии нами предполагалась в 2,5 раза выше, чем в пятом, а процент по депозитам на 1% выше. Однако решающее значение в формировании более благоприятного климата для окупаемости инвестиций в восьмом сценарии сыграл более короткий период «оборачиваемости» производимых инвестиций (в наших расчетах он на восемь лет меньше, чем в пятом сценарии). Сама структура дисконтирования доходов и издержек отрицает целесообразность построения инвестиционных планов с чрезмерно длительным периодом окупаемости приобретаемого в процессе обучения человеческого капитала. Отсюда следует чрезвычайно важный вывод: при принятии решения об инвестировании в образование нельзя исходить из желания эксплуатировать полученные знания в течение слишком длительного периода времени (например, до момента выхода на пенсию). Иными словами, инвестор должен быть готов в определенный момент времени либо «списать» приобретенный в результате обучения человеческий капитал и полностью его обновить, либо эффективно «нарастить» его и продолжить его эксплуатацию на оставшемся отрезке жизненного пути.
Сделанный выше вывод позволяет прийти к довольно оптимистичному заключению по поводу того, что хорошо продуманные планы по занятию наукой и написанию кандидатских и докторских диссертаций могут дать хороший экономический эффект даже, если они осуществляются в зрелом возрасте (35-40 лет) с помощью кредитных средств. Такое положение дел оставляет достаточно стимулов для молодых людей при построении научной карьеры.
8. Роль государства в подготовке специалистов по «нерентабельным» профессиям
При переходе к доминированию платной формы обучения могут возникнуть следующие проблемы. Ряд профессий может попасть в группу принципиально нерентабельных. Это связано с двумя причинами. Во-первых, всегда имеются дорогостоящие профессии и специальности в том смысле, что обучение им предполагает повышенные траты. Например, совершенно очевидно, что подготовка астрофизика предполагает более высокую «наукоемкость», нежели подготовка юриста. Так, если для первого требуется не только квалифицированный преподавательский состав, но и солидная материальная база, то для второго используется в основном только живой труд лекторов. Данный факт приводит к тому, что плата за обучение по специальности астрофизика будет объективно выше, чем по специальности юриста. Во-вторых, всегда существует целый ряд «нерыночных» профессий и видов деятельности, что не позволяет соответствующим специалистам рассчитывать на высокую оплату своего труда. Продолжая предыдущий пример, можно констатировать, что даже очень опытный астрофизик, как правило, не может рассчитывать даже на заработок начинающего юриста.
Подобное положение дел в условиях платного образования приведет к полному параличу целого ряда важнейших профессий. К примеру, дипломированный астрофизик будет наталкиваться на два препятствия, проявляющихся на разных временных горизонтах – краткосрочном и долгосрочном. Первое возникнет при невозможности расплатиться вовремя за взятый кредит, второе – при неудовлетворительной отдаче затрат на образование. Конечно, можно пустить события на самотек в надежде, что энтузиазм и альтруизм индивидов, желающих посвятить себя астрофизике, преодолеют возникающие трудности. Однако вряд ли такое решение можно считать оправданным. Что же можно сделать в подобной ситуации?
На наш взгляд, наряду с полным дотированием некоторых специальностей можно использовать следующий подход. С учетом складывающейся конъюнктуры государство может с помощью ориентировочных расчетов по формулам (15) и (18) очертить круг «неблагонадежных» профессий, подготовка по которым не может идти на основе рыночного инвестирования с использованием кредитов. В отношении таких профессий должна проводиться особая политика, предполагающая формирование государственных программ льготного кредитования образования. Параллельно необходимо пересматривать уровень заработков специалистов по данным профессиям на государственных предприятиях. На негосударственных объектах можно регламентировать нижнюю планку зарплаты данных специалистов. Выбор сроков кредитования, процентных ставок за кредит и величины зарплаты представителей «неблагонадежных» профессий можно осуществлять в результате итеративных расчетов по формулам (15) и (18) таким образом, чтобы были обеспечены, во-первых, возвратность кредитов, а во-вторых, приемлемая рентабельность вложений в обучение этим профессиям.
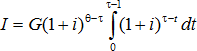
[1] Балацкий Е.В. Дисконт-фактор в расчетах рентабельности вложений в человеческий капитал// "Общество и экономика", №11-12, 2000.
[2] Беккер Г. Человеческий капитал. Главы из книги// "США: экономика, политика, идеология", №11, 1993.
[3] Капелюшников Р.И. Экономический подход Гэри Беккера к человеческому поведению// "США: экономика, политика, идеология", №11, 1993.
[4] Российский статистический ежегодник: Стат. сб. М.: Госкомстат России. 1999.


































Написать комментарий