Когда аналитики оценивают различные фискальные эффекты, то всегда возникает вопрос: насколько точны все эти расчеты? Что такое точки Лаффера и каковы их разновидности? Как их можно оценить? И как проверить то, насколько правильно проведены расчеты? Что такое инвариантность этих точек?
1. КРАТКАЯ ИСТОРИЯ ВОПРОСА
Интерес экономической науки к оптимальной настройке налоговой системы не уменьшается. Как правило, данная проблема решается путем отыскания так называемых лафферовых точек применительно к показателю общей налоговой нагрузки. Данное направление исследований само по себе является многообещающим, однако время показало методическую тупиковость большинства предлагаемых различными авторами моделей, методов и алгоритмов оценки точек Лаффера. Коснемся этого вопроса более подробно.
Насколько нам известно, само понятие точки Лаффера впервые в явной форме было введено С.В.Гусаковым и С.В.Жаком в работе [1]. Данный термин, будучи совершенно логичным, оказался довольно удачным и прочно вошел в современную теорию фискального регулирования. Однако позднее в работах [2] и [3] понятие точки Лаффера получило несколько иное содержательное наполнение, нежели то, которое изначально вкладывалось авторами [1]. Позднее, в работе [4] было проведено четкое разграничение между производственной и фискальной кривыми и уточнено исходное понятие точки Лаффера, в результате чего в научный оборот было введено понятие фискальных точек Лаффера 1-го и 2-го рода (их подробное определение будет дано ниже). В настоящее время указанная классификация может считаться общепринятой и окончательной. Это, разумеется, не означает, что эволюция понятия точки Лаффера на этом завершилась. Можно указать, в частности, на работу В.Г.Папавы [5], где традиционная фискальная кривая Лаффера, изображаемая на плоскости, дополняется фактором времени и располагается в трехмерном пространстве. По классификации В.Г.Папавы точка Лаффера 2-го рода в этом случае трансформируется либо в точку Балацкого, либо в точку Вишневского-Липницкого в зависимости от направления изменения фискального параметра. Однако в силу сложности восприятия и интерпретации «поверхности» Лаффера в трехмерном измерении и специфичности возникающих на ней экстремалий предложенные в [5] экономические категории пока не получили дальнейшего применения и развития.
Параллельно теоретической работе по уточнению понятия точки Лаффера велась и работа по ее количественной идентификации. Однако именно на этом пути встали самые серьезные проблемы. Дело в том, что аналитические модели и методы оценки точек Лаффера на практике дают, как правило, весьма странные результаты. В соответствии с ними точки Лаффера либо отсутствуют, либо имеют нереалистичные значения, либо неправдоподобно скачут по годам. Все это не может не настораживать при переходе к серьезным практическим расчетам.
Надо сказать, что перечисленные проблемы характерны как для оптимизационных, так и для дескриптивных моделей. При этом для оптимизационных моделей возникает дополнительная проблема субъективности выбора самого критерия оптимизации, изменение которого автоматически изменяет расчетные формулы для точек Лаффера и, разумеется, их количественные значения [2]. Таким образом, оптимизационным моделям имманентна проблема нарушения инвариантности (неизменности) лафферовых точек относительно критерия оптимизации. Для дескриптивных моделей проблема их верификации и оценки адекватности стоит не менее остро [3]. Если подобные модели игнорируют какие-то важные моменты динамики экономической системы, то они «рождают» совершенно бессмысленные точки Лаффера. Решить указанные проблемы оптимизационных и дескриптивных аналитических моделей в настоящее время не представляется возможным. Не исключено, что такого решения вообще не существует.
Желание избежать проблем, сопряженных с использованием аналитических моделей, привело к разработке вычислительных алгоритмов, направленных на механическое «нащупывание» точек Лаффера без глубокого содержательного наполнения. К числу таких алгоритмов можно отнести метод кусочной интерполяции, предложенный в [4]. Однако его массированное применение с использованием реальных статистических данных выявило абсолютную неустойчивость точек Лаффера, что ставит под сомнение целесообразность дальнейшего использования данного метода.
В русле подобных «механистических» исследований лежит и такой довольно экзотический метод, как графический [6]. Любопытно, что авторы данного метода ухитрились даже свои довольно простые теоретические рассуждения официально зарегистрировать в Международной регистрационной палате информационно-интеллектуальной новизны под названием замкнутой кривой Куликова-Павлова. Тем не менее, даже официальная регистрация подобных «открытий» не делает графический метод более весомым в глазах практиков, особенно если учесть, что авторы ограничились лишь беглой демонстрацией его работы на примере нескольких цифр. Все это отрицает возможность широкого тиражирования графического метода для обоснования оптимального налогового бремени.
Разумеется, перечисленными методами и моделями не исчерпывается все то инструментальное разнообразие, порожденное желанием отыскать такие «мифические» объекты, как точки Лаффера. Однако все методические инновации грешат одним и тем же недостатком – они не могут быть использованы на практике без сотни (а может быть, и тысячи) оговорок.
Сложившийся методический кризис привел к осознанию того, что практические расчеты должны базироваться все же на эконометрических моделях. В данном случае мы имеем в виду эконометрические модели в узком смысле слова, предполагающие построение регрессионных зависимостей на основе ретроспективных рядов. Надо сказать, что данные модели не пользуются большой популярностью и любовью среди экономистов-теоретиков (а поиски точек Лаффера – это, безусловно, епархия теоретиков), занимающихся математическим моделированием экономики. Они, скорее, мирятся с этими моделями из-за отсутствия какой-либо альтернативы. Видимо этим фактом и объясняется то, что создание первых эконометрических моделей, предназначенных для оценки точек Лаффера, исторически началось уже после того, как теоретики всесторонне «изгрызли» эту проблему, разочаровались в ней и оставили ее для дальнейшего «раскалывания» специалистам по макрооцениванию.
В настоящее время стало совершенно очевидно, что расчетам точек Лаффера можно доверять только в том случае, если они основаны на квалифицированной обработке реальных статистических данных методами математической статистики. Однако здесь также имеются определенные вопросы.
2. ПРОБЛЕМА НАРУШЕНИЯ ИНВАРИАНТНОСТИ ТОЧЕК ЛАФФЕРА ПРИ ОСУЩЕСТВЛЕНИИ ЭКОНОМЕТРИЧЕСКИХ РАСЧЕТОВ
Одна из первых попыток эконометрической оценки точек Лаффера была предпринята в работе [7]. В ней, в частности, была предложена хорошо себя зарекомендовавшая в последующих расчетах базовая производственно-институциональная функция (ПИФ) следующего вида:

Особенность функции (1) заключается в том, что макропродукт страны зависит от труда, капитала и налогового бремени. Причем влияние труда и капитала на экономический рост само зависит от фискального климата. Более того, эластичность труда и капитала является квадратичной функцией налоговой нагрузки, что автоматически предопределяет нетривиальность всего анализа.
Функция (1) задает производственную кривую, т.е. зависимость между выпуском и налоговой нагрузкой. Тогда фискальная кривая, т.е. зависимость между массой собираемых налогов и относительной налоговой нагрузкой, описывается следующей функцией:

Стержневой идеей фискального анализа на базе ПИФ (1) и (2) является определение взаимного расположения точек Лаффера 1-го и 2-го рода и фактической величины налоговой нагрузки [7]. Рассмотрение данных трех фискальных индикаторов позволяет нарисовать довольно полную картину налогового климата и его роли в формировании динамики экономического роста.
Напомним, что фискальной точкой Лаффера 1-го рода q* называется вершина (т.е. точка максимума) производственной кривой (1), когда

Аналогичным образом определяется фискальная точка Лаффера 2-го рода q**, в качестве которой понимается вершина (т.е. точка максимума) фискальной кривой (2), когда
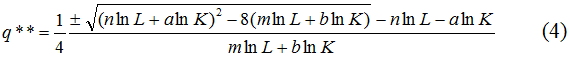
Формула (4) требует пояснений. Из двух стационарных точек, определяемых в соответствии с (4), выбирается только одна, являющаяся точкой максимума. Однако заранее сказать, какая их двух критических точек будет точкой максимума нельзя, в связи с чем в формуле (4) фигурируют две потенциальные точки Лаффера 2-го рода.
Так как правые части соотношений (3) и (4) зависят не только от параметров модели, но и от инструментальных переменных, в свою очередь зависящих от времени, то и сами точки Лаффера 1-го и 2-го рода не являются константами на всем интервале исследования. Наоборот, они оказываются «плавающими» во времени, что является большим плюсом проводимого анализа.
Прикладные расчеты, проведенные по формулам (1)-(4) для России, США, Швеции и Великобритании, дали очень обнадеживающие результаты как с точки зрения статистической значимости всех зависимостей, так и с точки зрения их содержательного наполнения [7]. В чем же тогда заключается вычислительная проблема, подлежащая обсуждению?
Первый класс проблем является чисто эконометрическим. В частности, существует опасность, что удлинение, укорачивание или сдвижка во времени исходного динамического ряда может привести к смещению параметров модели (1), что в свою очередь приведет к смещению значений точек Лаффера. Решить эту проблему может дальнейшее экспериментирование с моделью (1) и ее дополнительное тестирование.
Другая проблема, значительно реже обсуждаемая в качестве чисто эконометрической, заключается в том, что модель (1), позволяющая увязать выпуск (ВВП) и налоговое бремя не является единственной. Вполне возможно, что аналогичного результата можно добиться в рамках линейной, экспоненциальной или какой-либо еще модели. Причем статистические тесты у искомых моделей могут быть примерно одинаково хорошими. Однако при этом разные модели могут генерировать совершенно разные значения точек Лаффера, т.е. при переходе от одной эконометрической модели к другой будет нарушаться условие инвариантности (неизменности) точек Лаффера. Рассмотрим эту проблему более подробно.
В общем случае задача определения точек Лаффера ставится следующим образом. Имеется некая идеальная (гипотетическая) производственная кривая Лаффера, которую мы аппроксимируем определенной регрессионной функцией на основе эмпирических (отчетных) значений имеющихся переменных. Как предполагается, обе функции имеют точки максимума. Задача состоит в том, чтобы подобрать параметры регрессии таким образом, чтобы идеальная и регрессионная функции были максимально похожи и точки максимума на них по возможности совпадали.
Однако решение подобной задачи, как оказывается, не всегда возможно. Дело в том, что для хорошей аппроксимации необходимо, чтобы эмпирические точки q располагались на максимально большой области определения. Учитывая имеющийся перегиб в кривой Лаффера, эмпирические точки q должны группироваться вокруг точки Лаффера с обеих сторон от нее. Только в этом случае будет обеспечена информационная наполненность эконометрической зависимости, необходимая для корректных расчетов. Если же данное условие не выполнено и эмпирические значения q будут «кучковаться» только с одной стороны точки Лаффера, т.е. на левой (восходящей) или правой (нисходящей) ветви кривой Лаффера, то возникает проблема информационной недостаточности для эффективной идентификации искомой эконометрической зависимости.
В этом случае может оказаться, что эконометрическая функция будет очень хорошо аппроксимировать гипотетическую кривую Лаффера на имеющемся множестве эмпирических значений q, но точки Лаффера на этих двух кривых будут сильно смещены относительно друг друга.1 Графически этот эффект показан на рис.1, где Y0 – идеальная (аппроксимируемая) функция, Y1 – эконометрическая (аппроксимирующая) функция, q0 – истинная (гипотетическая) точка Лаффера, q1 – эмпирическая (идентифицированная) точка Лаффера; пунктирным облаком обозначена область скопления эмпирических точек q. В подобной ситуации значительное расхождение между гипотетической и аппроксимирующей функциями начинается лишь за пределами эмпирических наблюдений. Это означает, что расположение точки Лаффера определяющим образом зависит от вида функциональной зависимости, произвол выбора которой практически ничем не ограничен.
Рассмотренный эффект информационной недостаточности можно выразить и чисто математическим языком: если все эмпирические точки q расположены вдоль одной из ветвей гипотетической кривой Лаффера, то сама точка Лаффера определяется не процедурой интерполяции, а процедурой экстраполяции. Следовательно, ее значение зависит от произвола исследователя при выборе алгебраической формы аппроксимирующей кривой.
Экономическая интерпретация эффекта информационной недостаточности такова: для объективной оценки точки Лаффера необходимо, чтобы среди эмпирических данных о налоговой нагрузке были такие, которые превышают точку Лаффера, и такие, которые меньше ее. Иначе говоря, для точной идентификации точки Лаффера необходимо, чтобы изучаемая экономическая система в прошлом часть времени находилась в комфортном налоговом режиме (т.е. когда налоговая нагрузка меньше точки Лаффера), а часть времени – в режиме фискального «перебора» (когда налоговая нагрузка выше точки Лаффера). Из сказанного совершенно очевидно, что это не всегда возможно.
Резюмируя сказанное, можно констатировать следующее. Оценка точек Лаффера на основе эконометрических моделей возможна только при выполнении одного принципиального условия: информационное обеспечение расчетов должны быть таково, чтобы эмпирические точки q были «рассыпаны» с обеих сторон точки Лаффера.
Забегая немного вперед, укажем, что данное условие выполняется для экономики США, но не выполняется для российской экономики. Таким образом, существует целая группа стран, для которых использование эконометрического аппарата оказывается принципиально невозможным для определения точек Лаффера. В данном случае мы сталкиваемся с принципиальной ограниченностью самого эконометрического инструментария.
Если мы имеем дело с «неблагополучными» странами, для которых характерна проблема информационной недостаточности, то можно попытаться провести вычислительные эксперименты относительно различных аппроксимирующих функциональных зависимостей. Иногда разные классы моделей при более или менее одинаковом качестве (судя по соответствующим статистическим тестам) дают достаточно близкие значения точек Лаффера (такой результат был получен нами для российской экономики). Это позволяет с определенной степенью условности определить точки Лаффера, хотя в общем случае проблема информационной недостаточности все же остается.
Третья и наиболее интересная для нас проблема заключается в другом. Пусть мы правильно специфицировали модель и идеально идентифицировали ее параметры (т.е. две предыдущие проблемы решены). Но по своему содержанию модель (1) предполагает несколько способов учета макроэкономических факторов. Так, например, труд в базовом варианте учитывается в физическом выражении – как численность лиц, занятых в национальной экономике (L). Между тем учет фактора труда может производиться и стоимостной форме (W) – в виде затрат на оплату труда. В отношении другого макрофактора (капитала) возможны следующие вариации: основные производственные фонды (K) в стоимостном выражении и инвестиции в основные производственные фонды (I) в стоимостном выражении. Учитывая возможность попарной комбинации данных показателей, можно рассматривать четыре разновидности базовой модели (1): пары макрофакторов {K,L}, {I,L}, {K,W} и {I,W}.
Как правило, модель (1) «проходит» тесты по всем четырем модификациям. Тогда возникает вопрос: какая модель лучше?
Разумеется, подобный вопрос является болезненным не всегда. Если по различным модельным модификациям имеет место небольшой сдвиг точек Лаффера (а какой-то всегда имеется), то это позволяет очертить границы, в которых находятся искомые точки. В этом случае сами точки Лаффера становятся как бы размытыми и принимают интервальное значение. Если же наблюдается сильное расхождение лафферовых точек, то возникает дезориентация относительно их истинных значений. В этом случае, по-видимому, должна быть поставлена под вопрос сама возможность использования модели (1).
Таким образом, в практических расчетах при идентификации точек Лаффера по модели (1) необходимо проводить своеобразный тест на наличие их инвариантности при изменении способа учета макрофакторов. Только при успешном прохождении этого теста можно выносить окончательное суждение об истинном значении точек Лаффера.
Надо сказать, что рассмотренная проблема не может быть решена априорно. Нельзя сказать, что, например, показатель L лучше W или наоборот. В частности, W лучше улавливает уровень загрузки рабочей силы, т.к. он аккумулирует частичную и сверхурочную занятость. Вместе с тем показатель W необходимо дефлировать, приводя в соответствие с величиной выпуска (ВВП), что предъявляет дополнительные требования к исходной статистической информации. Аналогично другой пары можно сказать примерно то же. Показатель K учитывает всю массу средств производства, а не только те, которые были дополнительно задействованы в текущем году, однако переоценка фондов сама по себе представляет такую методическую и вычислительную проблему, которая обесценивает положительную содержательную «начинку» K.
Единственное, что можно сказать для сужения возможных расчетов, это то, что вычислительный приоритет должен быть отдан двум парам: {K,L} и {I,W}. Логика здесь проста: при вычислении основных фондов и численности занятости в одинаковой степени игнорируется степень загруженности макрофакторов. При использовании объема инвестиций в основной капитал и фонда оплаты труда в одинаковой степени учитываются текущие денежные затраты на оплату овеществленного и живого труда. В этом случае в неявной форме происходит учет интенсивности производства.
Таким образом, исследование проблемы инвариантности точек Лаффера может быть сведено к их сопоставлению для ресурсных пар {K,L} и {I,W} в рамках базовой модели (1); две другие пары могут быть использованы для получения вспомогательных модельных сценариев.
3. РЕЗУЛЬТАТЫ ЭМПИРИЧЕСКИХ РАСЧЕТОВ
Для проверки нашей гипотезы о возможном нарушении инвариантности точек Лаффера будем использовать данные по двум странам: США и России. Первая из названных стран характеризуется стабильной и чрезвычайно «правильной» (в смысле макропараметров) экономикой, вторая же, наоборот, дает классический пример неустойчивой экономической системы, «изломанной» во многих направлениях. Тест на инвариантность точек Лаффера применительно к таким разным странам позволяет достичь в наших исследованиях хорошей региональной репрезентативности.
Проведенные расчеты по базовой модели (1) применительно к экономике США дали следующие регрессионные модели:
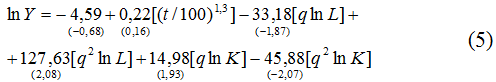
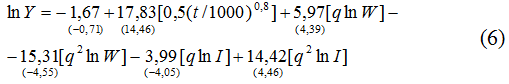
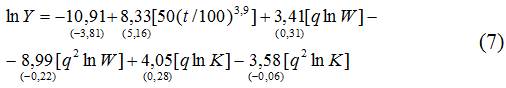
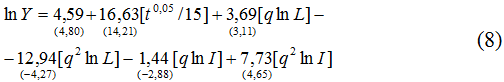
Как видно из уравнений (5)-(8), все построенные эконометрические модели отличались лишь способом учета научно-технического прогресса, в остальном они полностью соответствовали базовой зависимости (1). Кратко укажем, что все модификации (5)-(8) выдерживают основные статистические тесты и, следовательно, могут считаться статистически значимыми (в скобках под коэффициентами регрессии указаны значения их t-статистик; под уравнениями регрессии приведены коэффициенты детерминации и Дарбина-Уотсона). Таким образом, все они позволяют переходить к дальнейшим расчетам точек Лаффера 1-го и 2-го рода (табл.1 и табл.2).
Детальный анализ налогового климата в США и особенностей эволюции их фискальной системы не входит в нашу задачу; частично эти вопросы были раскрыты в работе [7]. Предметом дальнейшего анализа является более узкая проблема, связанная с сопоставлением результатов, полученных по разным модельным сценариям (5)-(8). Такие сопоставления позволяют сделать ряд интересных выводов.
Во-первых, сравнение двух базовых сценариев {L,K} и {W,I} между собой показывает, что переход от одного способа учета макрофакторов к другому практически не меняет значений точек Лаффера 1-го и 2-го рода. Таким образом, можно говорить об инвариантности лафферовых точек относительно двух основных способов учета макроресурсов в модели (1).
| Год | Сценарий {L,K} | Сценарий {W,I} | Фактическая налоговая нагрузка (q) | ||
|---|---|---|---|---|---|
| Точка Лаффера 1-го рода (q*) | Точка Лаффера 2-го рода (q**) | Точка Лаффера 1-го рода (q*) | Точка Лаффера 2-го рода (q**) | ||
| 1986 | 27,36 | 28,35 | 27,48 | 28,75 | 27,10 |
| 1987 | 27,55 | 28,55 | 27,51 | 28,78 | 27,89 |
| 1988 | 27,82 | 28,82 | 27,59 | 28,87 | 27,62 |
| 1989 | 28,02 | 29,03 | 27,71 | 28,98 | 27,89 |
| 1990 | 28,11 | 29,12 | 27,74 | 29,03 | 27,70 |
| 1991 | 27,93 | 28,94 | 27,64 | 28,91 | 27,67 |
| 1992 | 27,92 | 28,92 | 27,77 | 29,06 | 27,61 |
| 1993 | 28,07 | 29,08 | 27,96 | 29,25 | 27,97 |
| 1994 | 28,36 | 29,37 | 28,15 | 29,45 | 28,25 |
| 1995 | 28,59 | 29,61 | 28,32 | 29,62 | 28,61 |
| 1996 | 28,75 | 29,78 | 28,59 | 29,90 | 29,04 |
| 1997 | 28,98 | 30,01 | 28,79 | 30,11 | 29,33 |
| 1998 | 29,19 | 30,23 | 29,05 | 30,38 | 29,76 |
| 1999 | 29,40 | 30,43 | 29,28 | 30,62 | 30,06 |
| 2000 | 29,57 | 30,61 | 29,52 | 30,87 | 30,63 |
Для иллюстрации сказанного укажем, что максимальное расхождение между точками Лаффера 1-го рода в двух сценариях составляет всего лишь 0,37 процентных пункта, а минимальное – 0,04. Относительно точки Лаффера 2-го рода подобные расхождения составляют соответственно 0,40 и 0,03 процентных пункта. Полагая, что истинные значения точек Лаффера лежат где-то между сценарными оценками, возможные погрешности модельных расчетов исчисляются в долях процента ВВП (до 0,2%), что по всем меркам можно считать очень хорошим результатом. Данный факт и позволяет констатировать инвариантность точек Лаффера относительно схемы учета макрофакторов.
| Год | Сценарий {W,K} | Сценарий {L,I} | Фактическая налоговая нагрузка (q) | ||
|---|---|---|---|---|---|
| Точка Лаффера 1-го рода (q*) | Точка Лаффера 2-го рода (q**) | Точка Лаффера 1-го рода (q*) | Точка Лаффера 2-го рода (q**) | ||
| 1986 | 27,82 | 28,52 | 25,70 | 29,45 | 27,10 |
| 1987 | 27,83 | 28,52 | 25,71 | 29,45 | 27,89 |
| 1988 | 27,83 | 28,52 | 25,81 | 29,54 | 27,62 |
| 1989 | 27,84 | 28,53 | 25,97 | 29,72 | 27,89 |
| 1990 | 27,85 | 28,54 | 25,99 | 29,73 | 27,70 |
| 1991 | 27,86 | 28,55 | 25,77 | 29,50 | 27,67 |
| 1992 | 27,87 | 28,56 | 26,03 | 29,78 | 27,61 |
| 1993 | 27,87 | 28,56 | 26,35 | 30,12 | 27,97 |
| 1994 | 27,87 | 28,55 | 26,70 | 30,49 | 28,25 |
| 1995 | 27,87 | 28,56 | 26,96 | 30,77 | 28,61 |
| 1996 | 27,87 | 28,56 | 27,47 | 31,31 | 29,04 |
| 1997 | 27,87 | 28,55 | 27,89 | 31,75 | 29,33 |
| 1998 | 27,86 | 28,55 | 28,44 | 32,34 | 29,76 |
| 1999 | 27,86 | 28,55 | 28,91 | 32,83 | 30,06 |
| 2000 | 27,87 | 28,55 | 29,39 | 33,34 | 30,63 |
Во-вторых, вспомогательные модельные сценарии {W,K} и {L,I} можно квалифицировать как «маргинальные» относительно базовых сценариев табл.1. Поясним сказанное. Дело в том, что в базовых сценариях точки Лаффера с течением времени медленно дрейфуют в сторону увеличения. Между тем сценарий {W,K} дает практически полностью стационарные лафферовы точки – изменения в их значениях идут на уровне второго знака после запятой, т.е. на уровне сотых долей процентного пункта (табл.2). Сценарий {L,I} наоборот фиксирует слишком резкую тенденцию роста лафферовых точек: для точки 1-го рода рост составил 3,7 процентного пункта за весь период исследования по сравнению с 2,2 в сценарии {L,K}, а для точки 2-го рода – 3,9 против 2,3 п.п. Таким образом, сценарий {L,I} систематически завышает уровень динамичности точек Лаффера, а сценарий {W,K} – систематически занижает. В этом смысле они образуют некие крайние оценки идентифицируемых фискальных показателей.
В-третьих, точки Лаффера в сценариях {W,K} и {L,I} в ряде случаев ощутимо отличаются от аналогичных оценок в сценариях {L,K} и {W,I}. Так, например, максимальное отклонение значений точки Лаффера 1-го рода в сценариях {L,I} и {L,K} составляет 2,16 п.п., а точки Лаффера 2-го рода – 2,73 п.п. Максимальные расхождения в точках Лаффера 1-го и 2-го рода в сценариях {W,K} и {L,K} составляют 1,70 и 2,06 п.п. соответственно. Как же оценивать подобные погрешности эконометрических расчетов?
Строго говоря, полученные цифры позволяют говорить об отсутствии инвариантности точек Лаффера в базовых и вспомогательных сценариях расчета. К примеру, расхождение в 2,73 п.п. в точках Лаффера 2-го рода в сценариях {L,I} и {L,K} составляет почти 9% от величины самой этой точки в сценарии {L,K}. Если, как и раньше, допустить, что истинное значение точки Лаффера лежит где-то посредине идентифицированного доверительного интервала, то и в этом случае ошибка в 4-5% представляется все же значительной. Однако если учесть, что подобная ошибка является абсолютным максимумом, который зафиксирован только для одного из пятнадцати анализируемых лет, то следует признать, что искажение оценок точек Лаффера в базовых и вспомогательных сценариях не является таким уж катастрофичным. Таким образом, можно говорить о наличии своего рода квазиинвариантности точек Лаффера.
В-четвертых, в табл.1 и табл.2 хорошо просматривается следующая закономерность: расхождение между точками Лаффера 2-го рода во всех сценариях больше, чем между точками Лаффера 1-го рода. Иными словами, неопределенность в оценке точек Лаффера 2-го рода больше, чем точек 1-го рода. Данный факт вполне соответствует теоретическому силлогизму: лафферова точка 1-го рода отражает реакцию производителя, а точка 2-го рода реакцию бюджета на реакцию производителя. Фигурально выражаясь, при формировании точки Лаффера 2-го рода происходит наложение двух неопределенностей
Подытоживая вышесказанное, можно утверждать, что предложенная в [7] модель (1) позволяет довольно точно диагностировать фискальный климат в США и оценивать фискальные точки Лаффера 1-го и 2-го рода. Наблюдаемая инвариантность эконометрических оценок для базовых сценариев {L,K} и {W,I} служит достаточным основанием для подобного заявления. Вспомогательные сценарии {W,K} и {L,I} могут использоваться для дополнительного качественного анализа, направленного на более четкое уяснение тенденции происходящих сдвигов в величине лафферовых точек (эту миссию, по-видимому, должен выполнять сценарий {L,I}) и их средних значений (своего рода точек притяжения) (эту функцию довольно хорошо выполняет сценарий {W,K}).
Теперь перейдем к экономике России. Проведенные расчеты привели к следующим эконометрическим зависимостям:
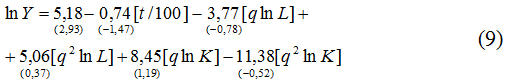
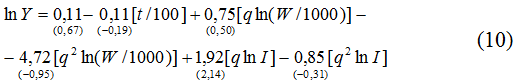
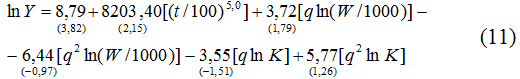
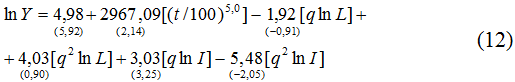
Как и в случае с США, все эконометрические модели (9)-(12) являются вполне надежными с точки зрения основных статистических параметров и позволяют осуществить оценку точек Лаффера (табл.3 и табл.4).
Прежде, чем переходить к анализу полученных результатов, сделаем одно важное замечание. Дело в том, что все четыре сценария {K,L}, {I,L}, {K,W} и {I,W} для экономики США, хотя и различаются конкретными числовыми данными, все же не противоречат друг другу. В данном случае мы подразумеваем, что показатели объема основного капитала и инвестиций в основной капитал имеют похожие временные траектории; показатели численности занятых и затрат на оплату труда изменяются тоже довольно синхронно. Следовательно, переход от одного показателя к другому не нарушает сложившихся тенденций в динамике макрофакторов. В этом случае довольно велика вероятность получения инвариантных оценок точек Лаффера, что и было зафиксировано табл.1. В отношении России ситуация значительно хуже. В частности, если показатели численности занятых и затрат на оплату труда движутся в унисон, то показатели объема основного капитала и инвестиций в основной капитал имеют прямо противоположные тенденции: первый постоянно рос, второй – падал. Уже один этот факт позволяет предположить, что оценки точек Лаффера по моделям (9)-(12), скорее всего, будут неинвариантными. Как же обстоит дело на самом деле?
Однозначный ответ на поставленный вопрос дают данные табл.3 и табл.4. В частности, они позволяют сделать следующие важные выводы.
Во-первых, сопоставление базовых сценариев {L,K} и {W,I} между собой показывает, что переход от одного способа учета макрофакторов к другому ведет к заметному смещению оценок точек Лаффера 1-го и 2-го рода. Таким образом, можно констатировать отсутствие инвариантности фискальных точек Лаффера относительно двух основных способов учета макроресурсов в модели (1).
Доказательством сказанного служат следующие цифры: максимальное расхождение между точками Лаффера 1-го рода в двух сценариях составляет 3,43 процентных пункта, а минимальное – 0,05. Для точки Лаффера 2-го рода подобные расхождения составляют соответственно 6,29 и 1,34 п.п. Полагая, как и раньше, что ошибка составляет примерно половину величины идентифицированного расхождения, следует признать, что погрешность в 1,7-3,1% ВВП является недопустимой. Действительно, такая «неувязка» эквивалентна примерно годовому или даже двухгодовому приросту ВВП страны (разумеется, если таковой происходит «естественными» темпами). На наш взгляд, можно мириться с вычислительными погрешностями в доли процента, но мириться с ошибками в проценты нельзя. Таким образом, для российской экономики точное значение точек Лаффера определить невозможно и приходиться довольствоваться лишь довольно широким интервалом, в котором они могут находиться.
| Год | Сценарий {L,K} | Сценарий {W,I} | Фактическая налоговая нагрузка (q) | ||
|---|---|---|---|---|---|
| Точка Лаффера 1-го рода (q*) | Точка Лаффера 2-го рода (q**) | Точка Лаффера 1-го рода (q*) | Точка Лаффера 2-го рода (q**) | ||
| 1989 | 36,59 | 46,22 | 33,91 | 40,48 | 30,95 |
| 1990 | 36,57 | 46,39 | 33,39 | 39,91 | 35,64 |
| 1991 | 36,55 | 46,67 | 33,12 | 39,80 | 32,19 |
| 1992 | 36,52 | 47,08 | 34,20 | 41,57 | 36,03 |
| 1993 | 36,49 | 47,44 | 33,90 | 41,42 | 29,53 |
| 1994 | 36,45 | 48,03 | 33,83 | 41,74 | 30,33 |
| 1995 | 36,44 | 48,15 | 36,37 | 44,68 | 26,27 |
| 1996 | 36,42 | 48,37 | 35,03 | 43,55 | 30,15 |
| 1997 | 36,38 | 48,94 | 34,76 | 43,34 | 33,39 |
| 1998 | 36,35 | 49,30 | 35,76 | 44,68 | 29,62 |
| 1999 | 36,42 | 48,32 | 37,94 | 46,98 | 31,39 |
| 2000 | 36,44 | 48,09 | 36,39 | 45,00 | 34,63 |
| Год | Сценарий {W,K} | Сценарий {L,I} | Фактическая налоговая нагрузка (q) | ||
|---|---|---|---|---|---|
| Точка Лаффера 1-го рода (q*) | Точка Лаффера 2-го рода (q**) | Точка Лаффера 1-го рода (q*) | Точка Лаффера 2-го рода (q**) | ||
| 1989 | 32,21 | 8,88 | 32,89 | 42,33 | 30,95 |
| 1990 | 32,27 | 9,02 | 32,88 | 42,30 | 35,64 |
| 1991 | 32,22 | 8,75 | 33,22 | 43,11 | 32,19 |
| 1992 | 31,86 | 7,53 | 34,78 | 46,60 | 36,03 |
| 1993 | 31,84 | 7,45 | 35,19 | 47,54 | 29,53 |
| 1994 | 31,74 | 7,16 | 36,40 | 50,16 | 30,33 |
| 1995 | 31,54 | 6,54 | 37,08 | 51,54 | 26,27 |
| 1996 | 31,56 | 6,60 | 38,70 | 54,74 | 30,15 |
| 1997 | 31,56 | 6,61 | 38,76 | 54,98 | 33,39 |
| 1998 | 31,47 | 6,34 | 39,99 | 57,38 | 29,62 |
| 1999 | 31,38 | 6,08 | 40,33 | 47,75 | 31,39 |
| 2000 | 31,49 | 6,40 | 38,67 | 54,61 | 34,63 |
Справедливости ради стоит заметить, что сдвиги в значениях точек Лаффера в двух базовых сценариях оказались не столь большими, как этого можно было ожидать, учитывая разнонаправленность изменений показателей K(t) и I(t). Хотя зафиксированные расхождения и не позволяют провести идентификацию лафферовых точек с высокой точностью, они все же не мешают пониманию качественной картины, так как результаты расчетов по базовым сценариям в принципе не противоречат друг другу. Такой результат является в значительной степени парадоксальным, так как изначально у нас не было надежды на то, что эконометрические методы обработки ретроспективных рядов смогут «справиться» со столь разными траекториями и свести их к единой базе.
Во-вторых, вспомогательные сценарии можно охарактеризовать как однозначно «бракованные». Поясним сказанное. Максимальное расхождение между точками Лаффера 1-го рода в сценариях {L,I} и {L,K} составляет 3,70 процентных пункта, а между точками Лаффера 2-го рода – 9,43 (для сценариев {L,I} и {W,I} данные характеристики еще хуже). Приведенные цифры недвусмысленно показывают, что ни о какой инвариантности точек Лаффера в данном случае говорить не приходиться. Сравнение же точек Лаффера 1-го рода в сценариях {W,K} и {L,K} дает максимальную невязку в 4,38 п.п., что делает сценарий {W,K} еще менее достоверным. Что касается точки Лаффера 2-го рода, то она в данном сценарии вообще является вырожденной. Это следует из того, что ее значение меньше точки Лаффера 1-го рода, а это противоречит основному теоретическому постулату о взаимном расположении точек Лаффера. Таким образом, вспомогательные модельные сценарии несут информацию, доверять которой без серьезных оговорок вряд ли возможно.
В-третьих, как и в случае с США для российской экономики имеет место явная закономерность: расхождение между точками Лаффера 2-го рода во всех сценариях примерно в 2-3 раза больше, чем между точками Лаффера 1-го рода (не считая вырожденного случая в сценарии {W,K}). Это означает, что если реакцию производителя еще как-то можно предсказать, то реакция бюджета совершенно непостижима.
4. ОСМЫСЛЕНИЕ РЕЗУЛЬТАТОВ
Все вышеизложенное требует основательного переосмысления. Выводы, которые надлежит сделать, далеко выходят за пределы конкретных экономик, рассматриваемых в статье. Пожалуй, не будет ошибкой сказать, что эти выводы выходят далеко и за пределы конкретных моделей экономического роста. Суммируем все методологические тезисы в несколько групп.
Во-первых, при построении эконометрических зависимостей типа производственно-институциональной функции (1) следует использовать два варианта учета макрофакторов: {W,I} и {L,K}. «Смешанные» способы учета {L,I} и {W,K}, как правило, дают значительно худшие результаты при вычислении таких «вторичных» экономических индикаторов, как точки Лаффера 1-го и 2-го рода. Не исключено, что данная закономерность распространяется и на другие «вторичные» характеристики. На практике, видимо, можно смело отбрасывать «смешанные» схемы {L,I} и {W,K} и концентрировать все внимание только на базовых модельных сценариях {W,I} и {L,K}.
Во-вторых, проведенные расчеты убедительно доказали, что проблема инвариантности точек Лаффера при смене схемы учета макрофакторов, входящих в эконометрическую производственно-институциональную функцию, ни в коем случае не является надуманной проблемой. Наоборот, наличие этой проблемы приводит к чрезвычайно сильному урезанию области применения эконометрических методов к оценке лафферовых эффектов. По сути дела, мы выявили, что эконометрический аппарат приложим лишь к очень гармоничным экономикам типа американской. Менее сбалансированные экономические системы наподобие российской экономики несут в себе некий структурный изъян, который не проявляется на стадии построения и калибровки эконометрических моделей, но сказывается на их последующем использовании для вычисления ключевых «вторичных» макроэкономических индикаторов. В этом пункте мы сталкиваемся с принципиальными ограничениями, накладываемыми на использование эконометрических методов для оценки фискальных точек Лаффера.
В-третьих, даже отсутствие инвариантности точек Лаффера не означает их абсолютной бесполезности, ибо они могут быть использованы для качественного анализа ситуации. Действительно, если для России использовать только базовые сценарии {W,I} и {L,K}, то, например, в 1989 г. точка Лаффера 1-го рода лежала в интервале 33,9-36,6%, а в 2000 г. она определялась вообще очень точно – в районе 36,4%. В эти же годы точка Лаффера 2-го рода располагалась в диапазонах 40,5-46,2% и 45,0-48,1%. Даже этих данных достаточно, чтобы определить, что в 1989 г. точка Лаффера 1-го рода лежала явно выше фактического налогового бремени, а в 2000 г. – немного ниже. В отношении же точки Лаффера 2-го рода можно утверждать, что ее значение превышало возможную разумную налоговую нагрузку (особенно это справедливо для 2000 г.). Таким образом, для диагностики принципиальных моментов в развитии фискальной системы эконометрическая модель (1) может быть весьма полезна.
В-четвертых, анализ показал, что роль и значение точки Лаффера 1-го рода как макроэкономического индикатора выше, чем точки Лаффера 2-го рода. Этот вывод представляется достаточно важным, так как в традиционной концепции кривой Лаффера интерес сосредоточен как раз на точке 2-го рода. Сделанное теоретическое уточнение является совершенно естественным, если учесть, что на практике, как правило, «конкуренция» идет между точками Лаффера 1-го рода и фактической налоговой нагрузкой (т.е. при определении, что выше); точка Лаффера 2-го рода в основном сильно смещена вверх в область малореалистичных фискальных значений (как, например, в России). Исключения составляют только особые случаи, как в США, когда точки Лаффера 1-го и 2-го рода почти «слипались» (зазор между ними составлял всего лишь 1%), а фактическая налоговая нагрузка флуктуировала между ними и в их окрестности. Однако подобные примеры являются большой редкостью.
В-пятых, идентификация точки Лаффера 1-го рода q* на основе (1) должна сопровождаться проверкой ее расположения относительно фактических значений налоговой нагрузки q. Если точка Лаффера q* «зацентрована» между эмпирическими точками налоговой нагрузки q, то построенная эконометрическая модель, грубо говоря, имеет право на существование. В противном случае построенная модель должна быть отвергнута и проведена очередная итерация по ее спецификации и калибровке.
Подводя итоги сказанному, следует сказать, что проблема инвариантности фискальных точек Лаффера является частной проблемой современной практики макроэкономического оценивания. Применительно к другим эконометрическим зависимостям будут «вылезать» и другие постановки проблемы инвариантности макрооценок. Главный же результат проделанной нами работы заключается в том, что подводит к осознанию того факта, что многие самые тонкие макроэкономические расчеты, базирующиеся на ультрасовременном модельном и техническом инструментарии, на самом деле грешат существенными ошибками. Чтобы избежать таких ошибок, на практике необходимо проводить дополнительные расчеты, что в дальнейшем процедуру макроэкономического оценивания сделает еще более трудоемкой.
- Гусаков С.В., Жак С.В. Оптимальные равновесные цены и точка Лаффера// «Экономика и математические методы», №4, 1995.
- Балацкий Е.В. Лафферовы эффекты и финансовые критерии экономической деятельности// «Мировая экономика и международные отношения», №11, 1997.
- Балацкий Е.В. Точки Лаффера и их количественная оценка// «Мировая экономика и международные отношения», №12, 1997.
- Балацкий Е.В. Эффективность фискальной политики государства// «Проблемы прогнозирования», №5, 2000.
- Папава В.Г. Лафферов эффект с последействием// «Мировая экономика и международные отношения», №7, 2001.
- Куликов А.Г., Павлов И.П. Графический метод расчета ВВП и поступления налогов в бюджет// «Финансы», №5, 2000.
- Балацкий Е.В. Анализ влияния налоговой нагрузки на экономический рост с помощью производственно-институциональных функций// «Проблемы прогнозирования», №2, 2003.



































Написать комментарий