Рынок энергетики лежит в основе всей мировой экономики и политики. Именно поэтому прогнозы сдвигов на этом рынке имеют огромное значение для всех экономических агентов. Но как следует прогнозировать эти изменения? Какие методы и инструменты применяются в мировой практике? Насколько они эффективны и перспективны? Какие здесь имеются проблемы?
1. Введение
Прогнозирование рынка производства и потребления энергии имеет большое значение для мировой и национальных экономик. Однако в части существующих методов, инструментов и подходов к прогнозированию наблюдается довольно противоречивая ситуация. С одной стороны работа по прогнозированию ведется полным ходом, с другой – она находится в архаичном состоянии. Это связано с использованием простых и не слишком адекватных прогнозных методик, которые в основном представляют собой механистические процедуры, не учитывающие качественные события на рынке. И в этом не следует усматривать виду разработчика. Дело в том, что в последнее время рынок производства и потребления энергии претерпевает такие качественные изменения, которые никакими формальными количественными методами адекватно отразить нельзя.
Однако имеется и еще одно интересное свойство рынка энергетических прогнозов: с одной стороны все прогнозы широко демонстрируются, тиражируются, пропагандируются и рекламируются, с другой – вся их методическая часть тщательно скрывается от широкой общественности, в том числе от научной общественности. На наш взгляд, это связано с двумя причинами. Первая почти самоочевидная состоит в том, что хорошая работоспособная методика прогнозирования, доведенная до программной реализации, является коммерческим продуктом с довольно большими затратами. Обнародование методики автоматически лишает ее владельца не только прибылей, но и средств на возмещение расходов по ее созданию. Вторая причина состоит в том, что, как уже отмечалось, почти все прогнозные методики являются довольно примитивными, эклектичными, основанными на неких эвристических процедурах, которой бывает даже сложно обосновать. Все это приводит к тому, что обнародование практически любой методики тотчас вызовет убийственную критику со стороны академического сообщества, что будет способствовать дезавуированию и обесценению прогнозного продукта.
Данные обстоятельства необходимо иметь ввиду не только при проведении самостоятельных прогнозов, но и при анализе уже существующих подходов.
Помимо этого следует учитывать тот факт, что прогнозирование рынка энергоресурсов предполагает, по крайней мере, три главных агрегата: объем производства, спрос (продажи) и цены энергоресурсов. Эти агрегаты несопоставимы с точки зрения прогнозирования. Если первые два показателя следуют довольно-таки монотонным тенденциям, которые вполне возможно уловить и предугадать, то цены подвержены высокой волатильности и плохо поддаются долгосрочному прогнозированию. Ниже мы сфокусируем внимание в основном на производстве и потреблении энергоресурсов.
2. Методы экстраполяции
Большой класс моделей прогнозирования образуют методы экстраполяции. Можно даже сказать, что этот метод является доминирующим. В этой группе методов можно выделить несколько подходов, имеющих свою специфику. Рассмотрим некоторые из них более подробно.
Индексный метод. В простейшем случае прогноз емкости энергетического рынка Q осуществляется по следующей формуле:

Данный подход предполагает определение общего тренда в долгосрочной перспективе и не учитывает краткосрочных колебаний конъюнктуры. В рыночных условиях потребление электротехнической продукции в России может показывать высокую нестабильность. Так, волатильность спроса на отдельные виды электротехнической продукции может достигать 30% [1]. В зависимости от задач прогнозирования такие «потери» в реальной динамике экономического агрегата могут считаться недопустимыми.
Метод экспоненциального сглаживания. В данном случае подразумевается некая адаптивная процедура, в которой прогнозная величина зависит от предыдущего прогноза и реального положения дел. Расчеты производятся по следующей формуле [2]:
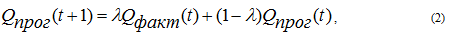
Модель (2) довольно примитивна и используется лишь в простейших задачах прогнозирования, например, для формирования «черновых» прогнозов. Для более полного учета обстоятельств прогнозирования рекомендуется осуществлять так называемую декомпозицию временного ряда, выделяя три его элемента – тренд, циклическую и случайную составляющие. С этой целью используют метод Хольта, учитывающий тренд изучаемого процесса, метод Брауна (частный случай метода Хольта) и метод Винтерса, который «цепляет» еще и сезонную составляющую [2]. Однако все эти способы сглаживания довольно примитивны и имеют ограниченную зону применения.
Иногда для учета колебаний в объемах производства и потребления аналитики строят «календари» процесса, которые отражают соответствующие подъемы и спады либо на качественном, либо на количественном уровне [3]. Модель, учитывающая колебательные особенности рынка энергетики была, в частности, реализована в России с помощью программной платформы «Deductor Studio» [3].
Регрессионные модели. В ряде случаев при прогнозировании рынка энергетики используются простые регрессионные модели. Наиболее ярким примером такой техники может служить подход, используемый Министерством энергетики США (US Department of Energy, DOE). В прогнозной системе этой организации внешними (экзогенными) параметрами являются показатели экономического и демографического роста по отдельным странам, которые, в свою очередь, также являются результатом прогнозирования. Эти показатели моделируются независимо от энергетического блока в разрезе регионов мира, а также мирового спроса на отдельные виды энергоресурсов. Далее на основе этих величин строится линейная зависимость между относительным приращением потребления энергии (Q) и ВВП (Y) с коэффициентом эластичности (пропорциональности): dQ/Q=θ(dY/Y) [4]. При построении линейной регрессионной модели используется следующий ее вид:

Характерно, что θ1990=0,78; в прогнозных расчетах DOE также фигурирует θ<1.
Таким образом, относительно хорошо прогнозируемый показатель ВВП выступает в качестве объясняющей переменной в регрессии (3) и позволяет делать прогнозные оценки в отношении энергопотребления в разрезе стран и регионов мира. Тем не менее, очевидно, что такой подход обладает явной ущербностью в силу своей «вторичности». Согласно такой методологии есть «первичный» прогноз ВВП, отталкиваясь от которого формируется «вторичный» прогноз энергопотребления и производства [6]. Ошибка в «первичном» прогнозе автоматически влечет за собой соответствующую ошибку во «вторичном» прогнозе.
Несмотря на простоту рассмотренных трех подходов, все даже довольно сложные прогнозные процедуры представляют собой лишь их комбинацию и модификацию. Можно сказать, что методы экстраполяции ограничиваются этими тремя «китами», которых на практике оказывается достаточно. Более того, все энергетические прогнозы носят сценарный характер, при этом роль базового сценария играет тот, при котором все темповые характеристики на перспективу берутся такими же, как и в ретроспективе [6]. Тем самым для базового сценария почти во всех прогнозных системах используется индексный метод.
3. Поведенческие модели
Главный недостаток методов экстраполяции состоит в отсутствии в них обратных связей. Для устранения этого недостатка разрабатываются сложные модели, учитывающие взаимные связи между многими переменными. С определенной степенью условности можно выделять две группы подобного рода моделей.
Нейронные сети. В основе этой методологии лежит представление, что нервная система и мозг человека состоят из нейронов, соединенных между собой нервными волокнами. Нервные волокна способны передавать электрические импульсы между нейронами. Все процессы передачи раздражений реализованы в живом организме как передача электрических импульсов между нейронами. Строение биологического нейрона таково: каждый нейрон имеет отростки нервных волокон двух типов – дендриты, по которым принимаются импульсы, и единственный аксон, по которому нейрон может передавать импульс; аксон контактирует с дендритами других нейронов через специальные образования – синапсы, которые влияют на силу импульса (рис.1) [5].
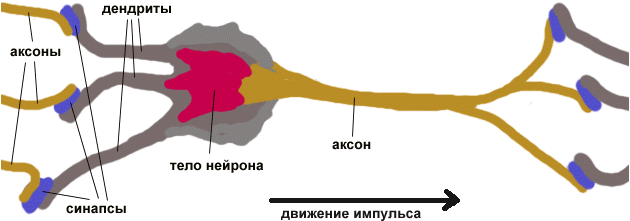
Рис.1. Общий вид нейронной сети.
Иногда полагают, что при прохождении синапса сила импульса меняется в определенное число раз, которое называется весом синапса. Импульсы, поступившие к нейрону одновременно по нескольким дендритам, суммируются. Если суммарный импульс превышает некоторый порог, нейрон возбуждается, формирует собственный импульс и передает его далее по аксону. Важно отметить, что веса синапсов могут изменяться со временем, а значит, меняется и поведение соответствующего нейрона. Схема описанного процесса приведена на рис.2 [5].
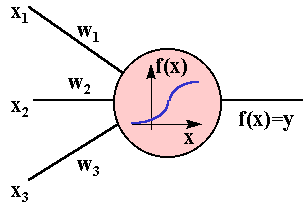
Рис.2. Структурная схема нейронной сети.
Логика работы модели нейрона с тремя входами (дендритами) показана на рис.2, где синапсы дендритов имеют веса w1, w2, w3. Пусть к синапсам поступают импульсы силы x1, x2, x3 соответственно, тогда после прохождения синапсов и дендритов к нейрону поступают импульсы w1x1, w2x2, w3x3. Нейрон преобразует полученный суммарный импульс
Как правило, передаточные функции всех нейронов в нейронной сети фиксированы, а веса являются параметрами нейронной сети и могут изменяться. Некоторые входы нейронов помечены как внешние входы нейронной сети, а некоторые выходы – как внешние выходы сети. Подавая любые числа на входы нейронной сети, мы получаем какой-то набор чисел на выходах нейронной сети. Таким образом, работа нейронной сети состоит в преобразовании известного входного вектора в известный выходной вектор при заданном преобразователе y=f(x), т.е. преобразование задается весами нейронной сети. Соответственно «обучить» выбранную нейронную сеть означает подобрать такие значения ее весов, чтобы она работала нужным образом. Так как имеется множество специальных алгоритмов по решению подобной задачи, то сама процедура моделирования рынка энергоресурсов в терминах нейронной сети имеет смысл. Однако, как показывает опыт, аппарат нейронных сетей успешно применяется для локальных энергорынков; для мирового рынка энергетики он пока не находит широкого применения.
Главный недостаток нейронной сети состоит в неустойчивости весовых коэффициентов для сложных систем. Соответственно прогнозировать поведение системы на основе «старых» весовых коэффициентов можно лишь с очень большой осторожностью.
Имитационные модели. Есть и другой способ учета прямых и обратных связей в системе – построение имитационных моделей, представляющих собой систему функциональных связей между ключевыми переменными. Например, отрасль энергетики имеет ряд особенностей, связанных с деятельность предприятий в условиях рыночной (конкурентной) среды. Согласно концепции М.Портера, интенсивность и состояние конкуренции, например, в электротехнической отрасли определяется совокупностью пяти сил: производитель; поставщик; потребитель; конкуренты; товары-заменители (рис.3).
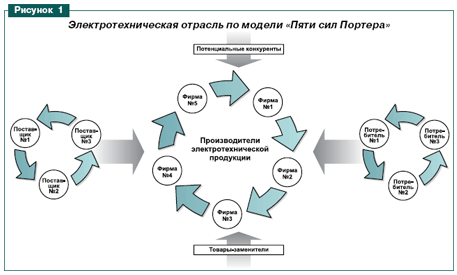
Рис.3. Схема «пяти сил Портера».
Такая поведенческая модель «Пяти сил Портера» позволяет в дальнейшем изучать возможные последствия при изменении исходного соотношения сил. Подобная модель и оценка работоспособности методики прогнозирования на ее основе была выполнена для российского рынка электротехнических сталей [1]. Однако для глобальных энергетических прогнозов такая схема пока не применялась, по-видимому, из-за сложности учета всех агентов схемы Портера.
4. Моделирование технологических сдвигов
В последнее время большое значение приобретают альтернативные виды энергии – солнечная, ветровая, отчасти туда же относится биотопливо и т.п. Можно говорить и об альтернативных способах производства традиционных энергоресурсов, например, сланцевом методе добычи газа. Такие технологические сдвиги слабо воздействуют на общий баланс производства и потребления энергии, но сильно влияют на объемы производства и потребления энергии в рамках тех или иных технологий и видов топлива, вызывая к жизни эффект замещения.
Учет такого рода сдвигов направлен на уяснение качественных сдвигов внутри мирового энергетического баланса. В свою очередь подобные сдвиги могут вести к принципиальным геополитическим перестановкам на мировой арене. Частным случаем учета эффекта замещения может служить схема расчета по вытеснению российской нефти европейским биотопливом с рынка Европы [7]. В этом случае спрос на сырую нефть (Qнеф) оценивается по формуле:

Расчеты, проведенные А.Б.Гусевым по формуле (4) показывают, что развитие биотопливного производства в Европе чревато для России тем, что уже через 15 лет европейские страны смогут полностью отказаться от российских поставок нефти [7]. Тем самым даже столь простые экстраполяции позволяют уяснить возможные глобальные рокировки на рынке энергоресурсов.
Иногда рассматриваются и более сложные процессы замещения. Например, в странах Европы намечается постепенный вывод атомных электростанций (АЭС) в противоположность российским тенденциям, где предполагается увеличение атомных мощностей. Кроме того, в Европе предусмотрена естественная убыль мощностей выработки электрической энергии на парогазовых ТЭС. Убыль указанных мощностей покрывается развитием нетрадиционной энергетики WАЛЬТ.
Считается, что объем мощностей WАЛЬТ изменяется согласно логистической кривой. Исходя из имеющихся данных о темпах роста WАЛЬТ и темпах роста населения А.И.Глаголев, С.С.Демин и Ю.Н.Орлов приближенно оценили величину WАЛЬТ по формуле [6]:
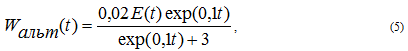
Хотя подобные схемы расчета эффекта замещения пока не нашли широкого распространения, они, судя по всему, являются очень перспективными.
5. Экспертные оценки
Помимо формальных и полуформальных методов в прогнозах рынка энергоресурсов широко используются эспертные оценки. Например, прогнозной системе WEPS (World Energy Projection System), лежащей в в основе прогнозов DOE, экзогенными параметрами являются экономический рост и демографический прогноз по странам, тогда основной параметр – это экспертная оценка роста потребностей в энергии в целом. Этот параметр не является, вообще говоря, независимым от прогнозируемых величин, но в этой модели он представлен как внешний, фиксированный для каждого сценария [6]. Выходными данными являются макроэкономические параметры по странам, включая спрос и предложение различных видов энергоресурсов. Таким образом, агрегатный спрос энергопотребления определяется на основе интуитивных представлений экспертов о перспективах развития рынка. В дальнейшем эта величина дробится на разные более мелкие агрегаты на базе простых вычислительных процедур.
Надо сказать, что подобные экспертные оценки средней скорости изменения потребления энергии, например, на 20-летнем отрезке времени базируются на представлениях о тренде энергопотребления. Между тем такая оценка является очень уязвимой, поскольку на глобальном уровне темп роста потребления энергии связан с изменением темпов роста численности населения, причем эта зависимость, по последним данным, не линейна, а приближенно квадратична. Кроме того, в разных регионах земного шара рост численности и рост потребностей неравномерен. Поэтому желателен более точный прогноз, учитывающий неравномерность развития отдельных региональных энергетических рынков.
6. Точность общемировых энергетических прогнозов
Простота моделей прогнозирования рынка энергетики инициирует простой вопрос: насколько можно доверять существующим прогнозам? Насколько эффективными вообще могут считаться имеющиеся прогнозные процедуры?
Расхождения между прогнозом и реальностью. На данные вопросы в литературе уже имеются более или менее определенные ответы. Так, исследование точности прогнозов Международного энергетического агентства (International Energy Agency, IEA) и Министерства энергетики США (US Department of Energy, DOE) показывает, что она может считаться вполне приемлемой [4].
| Прогнозный агрегат | Прогноз (год составления прогноза) | Факт | |||
|---|---|---|---|---|---|
| 1990 | 1991 | 1992 | 1993 | ||
| Потребление энергии в мире в 1995 г., QBTU* | 383 | 374 | 377 | 375 | 366 |
| Потребление энергии в мире в 2000 г., QBTU | 408 | 402 | 410 | 410 | 400 |
Так, из табл.1 видно, что в целом в конце 20 века DOE несколько переоценивало возможности рынка энергопотребления, однако эта ошибка не была фатальной. Максимальная погрешность для прогноза на 1995 год составила 4,6%, минимальная – 2,2%. Для прогноза на 2000 год данные характеристики составили 2,5 и 0,5% соответственно. Такая точность может считаться вполне удовлетворительной. При этом все прогнозы DOE отличались повышенным оптимизмом; ни в один из годов не зафиксировано недооценки рынка – всегда только переоценка.
Прогнозы IEA демонстрируют примерно те же эффекты (табл.2). Например, погрешность здесь изменяется от 0,1% до 5,2%. При этом все прогнозы также, как и в случае с DOE, тяготеют к переоценке реальной ситуации в сторону завышения.
| Год, на который составлялся прогноз | Год выпуска прогноза | Средняя ошибка, % | ||||||
|---|---|---|---|---|---|---|---|---|
| 1993 | 1994 | 1995 | 1996 | 1998 | 2000 | 2002 | ||
| 1993 | 1,5 | 1,5 | ||||||
| 1994 | 2,3 | 2,0 | 2,2 | |||||
| 1995 | 1,5 | 1,2 | 0,7 | 1,1 | ||||
| 1996 | 0,1 | -0,1 | -0,6 | 0,6 | 0,3 | |||
| 1997 | 0,8 | 0,7 | 0,2 | 1,8 | 0,9 | |||
| 1998 | 2,0 | 2,0 | 1,5 | 3,4 | 2,6 | 2,3 | ||
| 1999 | 1,7 | 1,8 | 1,3 | 3,6 | 2,9 | 2,3 | ||
| 2000 | 0,9 | 1,0 | 0,6 | 3,2 | 2,5 | 0,9 | 1,5 | |
| 2001 | 2,7 | 3,0 | 2,5 | 5,1 | 4,2 | 2,6 | 3,4 | |
| 2002 | 2,8 | 3,0 | 2,6 | 5,1 | 4,1 | 2,6 | 2,6 | 3,3 |
| Средняя ошибка, % | 1,6 | 1,7 | 1,2 | 3,2 | 3,3 | 2,0 | 2,6 | 2,2 |
Любопытно, что приведенная в табл.2 относительная ошибка определена как разность между прогнозным и фактическим значениями энергопотребления, деленная на прогнозное значение. При таком определении за основу берется прогнозное значение, поскольку отклонение делится именно на прогноз, а фактическое значение приобретает смысл отклонения от «основы» (т.е. от прогноза). Таким образом, по своему смыслу эта величина показывает относительное отклонение реальности от прогноза [4]. Такой подход представляется неверным – имеет смысл рассматривать отклонения прогноза от реальности. Такая корректировка точности прогноза не является принципиальной, но с точки зрения методической строгости имеет значение.
Следует сразу оговориться, что отмеченная приемлемая точность прогнозов DOE и IEA объясняется отнюдь не совершенством прогнозных процедур, а характером прогнозируемых процессов. Статистика показывает, что тренды мирового потребления энергии в целом не подвержены резким скачкам. Такое «нескачкообразное» поведение рассматриваемых величин делает их прогнозирование достаточно «благодарным» занятием. Именно отсутствие в мировой энергетике каких-либо «катастрофических» изменений лежит в основе их относительно точных прогнозов.
В литературе уже предлагались некоторые показатели для оценки точности как отдельных прогнозов, так и всей прогнозной системы. Например, О.Ю.Аполонский и Ю.Н.Орлов предлагают следующую конструкцию [4]. Пусть прогнозом P(k,l) будем называть сформированный в год k набор из M значений прогнозируемой величины, соответствующих некоторым годам l(1), l(2),…, l(M). Рассматриваемая выборка из M лет представляет собой целочисленный вектор l=(l(1), l(2),…, l(M)). Например, запись P(2000,l) означает, что этот прогноз сформирован в 2000-ом году и содержит набор опорных прогнозных точек в соответствии с числом компонент вектора l. Если, в частности, этот прогноз сделан до 2020 года с интервалом в 5 лет, то вектор l имеет вид
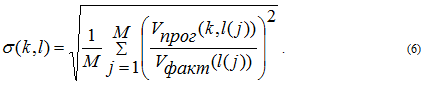
Заметим, что все сказанное справедливо только случаев, когда имеется только один сценарий прогноза или есть хотя бы базовый прогноз. В большинстве случаев используется множество (как правило, 3) сценариев, которые могут довольно сильно различаться между собой и давать совершенно разные ошибки от фактических параметров процесса. В этом случае необходимо «сводить» все прогнозные ошибки в один агрегатный показатель. В этих целях может использоваться формула (6), обобщенная для такого случая сложной прогнозной системы [4]. Надо сказать, что в целом проблема оценки точности сценарных прогнозов не только не решена, но и даже не ставится всерьез современным аналитическим сообществом.
Расхождения между разными прогнозными системами. Самостоятельную проблему представляет нестыковка прогнозов, выполненных разными организациями. Так, например, аналитики отмечают, что прогнозы потребления газа в Европе, выполненные разными компаниями, имеют расхождения друг с другом порядка 20%, как и декларируемая ими точность. Кроме того, прогнозы, выполненные одной и той же организацией в разное время, также отличаются – от нескольких процентов до тех же 15–20%, что существенно для долгосрочного анализа [4].
Для сравнения приведем данные по темпам роста потребления ТЭР, полученные в прогнозных системах, считающихся достаточно надежными (табл.3) [4].
| Год | IEO 2001 | IEO 2002 | DRI-WEFA | IEA | PIRA | PEL |
|---|---|---|---|---|---|---|
| 2010 | 1,1 (3,1) | 1,1 (3,0) | 1,1 (3,4) | 1,3 (2,8) | 0,7 (3,4) | 0,9 (1,5) |
| 2015 | 1,0 (3,3) | 1,0 (2,7) | 1,1 (3,6) | 1,2 (3,0) | 0,7 (3,3) | 0,8 (2,1) |
| 2020 | 0,9 (3,1) | 0,9 (2,5) | 1,0 (3,9) | 1,1 (3,1) | 0,6 (3,2) | 0,8 (2,7) |
Из табл.3 видно, что разброс в темпах прироста составляет по разным прогнозам более 50%, демонстрируя трудности при согласовании этих прогнозов. Следовательно, даже ведущие прогнозные системы пока не обладают возможностью настройки по входным данным других систем [4].
ЛИТЕРАТУРА
- Данилов Е. Методика прогнозирования российского электротехнического рынка// «Электротехнический рынок», №3(21), 2008 (www.market.elec.ru/nomer/20/forecasting-technique/).
- Исмагилов Т.С. Методы решения задачи прогнозирования в энергетике// «Вестник УГАТУ», Т.14, №4(39), 2010.
- Канторович С.А. Deductor Electra: Прогнозирование потребления электроэнергии/ BIGroup Labs (www.bigrouplabs.ru/Rech/plan/electraplan.html).
- Аполонский О.Ю., Орлов Ю.Н. Сравнительный анализ долгосрочных прогнозов развития мировой энергетики (www.keldysh.ru/papers/2007/prep26/prep2007_26.html).
- Аналитические технологии для прогнозирования и анализа данных (www.neuroproject.ru/forecasting_tutorial.php).
- Глаголев А.И., Демин С.С., Орлов Ю.Н. Долгосрочное прогнозирование газового рынка: опыт сценарного программирования. М.: Институт энергодиалога «Восток–Запад», 2003.
- Гусев А.Б. Биотопливо как инновационная перспектива российской энергетики// «Капитал страны», 01.07.2008 (www.kapital-rus.ru/index.php/articles/article/619).


































Написать комментарий