Массовая ипотека в России: модель развития
Какие модели ипотечного кредитования применялись в других странах, и что поможет запустить массовое ипотеку в России? Какую роль на рынке ипотечного кредитования могут сыграть ссудо-сберегательные программы и как они должны быть устроены?
Разработка и исследование ссудо-сберегательных программ ипотечного кредитования: динамическая модель
Предложена динамическая модель ссудо-сберегательной программы ипотечного кредитования (ССП). Введены понятия устойчивости и сильной устойчивости ссудо-сберегательных траекторий, порожденных ССП; получены необходимые и достаточные условия, гарантирующие выполнение этих свойств. Приведенные результаты расчетов показывают, что ССП обеспечивают устойчивое кредитование участников программы в достаточно широком диапазоне изменения параметров, близких к реальным.
1. Введение
Целью настоящей работы является создание математической модели, которая могла бы использоваться для разработки и анализассудо-сберегательных программипотечного кредитования (ССП). В работах Полтерович, Старков (2007, 2010) было показано, что в странах с несовершенными институтами и высоким отношением цены жилья к среднедушевому доходу внедрение именно таких программ целесообразно положить в основу стратегии развития массового рынка жилищного ипотечного кредитования. В настоящее время эта идея проходит апробацию в рамках так называемой «Народной ипотеки» (см., например, Михайлова, 2013, а также«Народная ипотека» на Дону... 2013). ССП характеризуются двумя принципиальными отличиями от других ипотечных институтов. Во-первых, выдача кредита в рамках этих программ обусловлена регулярным накоплением вкладчиком первоначального взноса в течение достаточно длительного времени (обычно 4-6 лет). Во-вторых, регулярное накопление стимулируется субсидиями из государственного (федерального или регионального) бюджета – премиями на стройсбережения. При этом вкладчики, нарушающие план накопления, лишаются премий, а при многократных нарушениях исключаются из программы вовсе. Благодаря этим особенностям а) ССП доступны для граждан с невысокими доходами; б) ненадежные заемщики выявляются уже на стадии накопления и не получают кредита; в) проценты по депозитам и кредиту могут быть достаточно низкими (обычно, 2-3% и 5-6%), так чтобы эффективный процент по депозитам с учетом премии оказался на достаточно высоком уровне, а ставка по кредиту привлекала вкладчиков и обеспечивала достаточно высокую маржу банку.
Вывод о целесообразности внедрения ССП базировался на изучении эволюции ипотечных институтов, на рассмотрении 125 эпизодов заимствования ипотечных институтов в 63 странах за 230 лет, на анализе недавнего опыта стран Восточной Европы и России, включая и кризисный период, и, наконец, на расчетах по математической модели на российских данных (Полтерович, Старков, 2007). В работе Полтерович, Старков (2010) было предложено начать формирование массовой ипотеки в России с эксперимента в одном из регионов.
ССП могут быть реализованы в рамках специализированных институтов – стройсберкасс (ССК) или строительно-сберегательных кооперативов, либо в форме специальных жилищных накопительных счетов в банке (ЖНС). Хотя в практике других стран ЖНС используются сравнительно редко, исследование, проведенное в Полтерович, Старков (2011), показало, что именно эта форма имеет наибольшие шансы на успех в современной России, поскольку ее внедрение связано с наименьшим сопротивлением заинтересованных игроков.
Идея построения экспериментальной системы ЖНС на уровне региона реализована администрацией Краснодарского края и Сбербанком РФ. К ноябрю 2012 г. около 4000 жителей края открыли жилищно-накопительные счета. При разработке этой системы нами была использована модель, близкая к изучаемой ниже (см. Ильинский, Полтерович, Старков, 2012).
Качество работы ССП зависит от сочетания значений экзогенных параметров и управляющих переменных. К первым относятся приток вкладчиков, процент по внешним кредитам, ставка резервирования, норма страховых отчислений, частота нарушений планов накопления, вероятность невыплаты кредита, доля друзей вкладчиков, распределение помесячных взносов вкладчиков, цены предпочитаемых ими квартир . К управляющим переменным относятся ставки по депозитам и кредитам, сроки накопления и кредитования, ставка премии на сбережения, предельный уровень премии в месяц. Управляющие переменные следует выбирать так, чтобы при изменениях экзогенных параметров в достаточно широком диапазоне обеспечить преимущество ССП перед альтернативными ипотечными программами для вкладчиков с невысокими доходами , банка и государства (региональной администрации или федерального центра). Такова первая и главная задача, стоящая перед разработчиком. Модель ССП должна предоставлять разработчику возможность решить эту задачу.
Вторая задача, тесно связанная с первой, состоит в том, чтобы обеспечить финансовую устойчивость ССП. Поясним это понятие.
При заданном наборе экзогенных параметров каждая ССП порождает ссудо-сберегательную траекторию (ССТ), характеризующуюся множествами вкладчиков, находящихся на той или иной стадии накопления и выплаты кредитов, суммами их средств на счетах, их задолженностей и т. п. ССТ допустима, если в каждый момент времени она предусматривает обязательства по кредитам, не превосходящие имеющихся денежных средств. Для обеспечения допустимости ССТ может оказаться необходимым либо создать очередь вкладчиков, выполнивших программу сбережений и ожидающих кредит, либо привлечь внешние займы. В этих случаях говорят о наличии кассового разрыва.Мы говорим, что ССТ финансово устойчива, если, начиная с некоторого момента времени, она обеспечивает положительную интегральную прибыль. ССТ финансово устойчива в сильном смысле, если она устойчива и не допускает финансовых разрывов вовсе, т. е. если она не предусматривает ни очередей, ни займов. Соответственно, СПП финансово устойчива (устойчива в сильном смысле), если в заданном диапазоне изменений экзогенных параметров устойчива (сильно устойчива) любая порожденная ею траектория. Модель должна позволить разработчику исследовать СПП на допустимость и финансовую устойчивость.
Очевидно, для решения сформулированных задач необходима динамическая модель ССП. Между тем, ни одна из известных нам прикладных моделей ССК не позволяет достаточно полно учесть переходную динамику, возникающую при изменении экзогенных параметров, в то время как именно такие изменения могут привести к кризису стройсберкасс. Поэтому на практике модели дополняются эвристическими процедурами для поддержания баланса в условиях существенного роста цен на жилье и нестабильности вступления в систему новых участников. Практически во всех известных нам работах предполагается, что параметры накопления и кредитования не меняются со временем, и анализируются соответствующие стационарные режимы (см., в частности, Laux (2005)). Статической является и модель, разработанная в монографии Полтерович, Старков (2007) для других целей.
Наиболее близкой к нашей является модель с перекрывающимися поколениями, использованная в статье Scholten (2000) для анализа простейшего типа ССП. Однако при анализе и в этом случае фактически рассматриваются только стационарные режимы. В этой модели все вкладчики одинаковы, их приток постоянен, не предусматривается бюджетная премия на сбережения, принято упрощенное правило назначения очередности при выдаче кредита (жребий).
Предлагаемая ниже модель (см. разделы 2,3) представляет собой систему нелинейных рекуррентных соотношений, описывающих динамику ССП (системы спецсчетов). Модель позволяет для каждого момента времени рассчитать число вкладчиков с разными сроками накопления, число вкладчиков, получивших право на кредит с разными сроками его ожидания, структуру внешних заимствований, число заемщиков, получивших кредиты в разное время, сумму, накопленную на депозитах, кредитную массу. При этом имеется возможность учесть изменения притока вкладчиков, наличие инфляции, изменения темпа роста доходов и ставок процента на внешнем рынке, а также вариации внутренних параметров спецсчетов: процентных ставок, сроков и объемов накопления и кредитования.
Благодаря этому модель дает возможность решать все три описанные выше задачи, и, таким образом, разрабатывать планы по накоплению и кредитованию участников ССП, устойчивые к колебаниям экзогенных параметров.
Модель включает в себя два важных частных случая, отражающие варианты ССП, используемые на практике:
- Строительно-сберегательная касса (ССК). В этом случае на социальные премии начисляется процент, текущая прибыль идёт частично в кредитную массу, частично выплачивается акционерам. Возможны очереди и займы под внешние проценты.
- Жилищно-накопительный счет в банке (спецсчет, ЖНС). В этом варианте нет процентов на социальные премии, нет очередей (кассовые разрывы покрывает банк), прибыль идёт банку.
В разделе 4 сформулированы условия финансовой устойчивости и сильной финансовой устойчивости ССП.В разделе 5 приведены результаты экспериментальных расчетов. Здесь исследованы границы финансовой устойчивости ССП.
Различные серии расчетов соответствовали различному выбору управляющих переменных (срок кредитования, величина дотации на сбережения, размер гарантированного кредита) и экзогенных параметров ( процент «друзей вкладчиков», рыночные ставки процента внешних заимствований и вложений). Кроме того, была исследована реакция ссудо-сберегательных траекторий на изменение внешних условий. При этом важнейшие параметры менялись достаточно резко и в широком диапазоне. В частности, рассматривалось падение притока вкладчиков на 50% и его полное прекращение.
Расчеты показали, что в российских условиях ССП обеспечивают устойчивое кредитование участников программы в широком диапазоне изменения внешних условий и внутренних параметров. При этом дефицит средств, приводящий к необходимости займов и возникновению очередей, наблюдается чаще не в стационарном, а в переходном режиме.
Последний результат явственно демонстрирует преимущество предлагаемой модели над известными, описывающими лишь стационарные режимы. Отсутствие длительного дефицита средств является важнейшей характеристикой ССП, характеризующей ее устойчивость: при высоком и длительном дефиците банк (или ССК) терпит убытки. А в случае невозможности обслужить потенциальных заемщиков возникает опасность массового «бегства вкладчиков». Стационарные модели дают чрезмерно оптимистические оценки и не позволяют получить своевременную информацию об угрозе кризиса.
2. Агенты ССП: общая схема взаимодействия
В данном разделе дается описание общей схемы взаимодействия участников ипотечной системы: потребителя, ссудо-сберегательного института (ССИ), банка и регионального или федерального правительства. Под ССИ здесь и далее подразумевается организация, которая занимается всеми операциями ССП: это может быть как сберегательный банк, так и специализированный банковский институт - ССК. Там где две модели различаются, будут делаться соответствующие оговорки.
Потребитель.
Потребитель, желающий приобрести жилье, обращается в ССИ для выбора ссудно-сберегательного плана. Его важнейшими характеристиками являются срок накопления (длительность ожидания жилья), срок кредитования, площадь приобретаемого жилья и размеры ежемесячных выплат при накоплении и при выплате кредита. В принципе, поведение потребителя можно описать стандартной моделью потребительского выбора. В данном случае она учитывала бы временные предпочтения агента и представляла бы собой задачу максимизации интегральной полезности при бюджетном ограничении с правой частью, равной части дохода, сберегаемой для покупки жилья. Из этой модели можно было бы определить спрос потребителей на квартиры той или иной площади. Однако выявление потребительских предпочтений – сложная задача. Поэтому мы будем предполагать заданным распределение потребителей по величине предпочитаемых ежемесячных выплат и предпочитаемому сроку накопления.
Потребитель, вступивший в ССП, может находиться в одной из трех стадий: накопление, очередь и выплата кредита.
а) Накопление.
Каждый месяц потребитель вносит сумму денег (взнос), не меньшую заранее оговоренной величины. На взнос ССИ начисляет процент по депозиту. Кроме того, с определенной периодичностью (обычно раз в месяц или в квартал) государство выплачивает потребителю премию (социальную выплату), пропорциональную сумме внесенных за период взносов.
b) Очередь.
В случае нехватки кредитной массы потребитель после окончания накопления может не получить кредит сразу, а оказаться в очереди за кредитом. Правила формирования очереди должны быть оговорены заранее.
На практике очередь может формироваться в рамках ССК, но обычно не предусматривается в рамках ЖНС.
c) Выплата кредита.
В течение срока кредитования агент ежемесячно вносит платежи за кредит. После завершения выплат по кредиту он выходит из системы с приобретенным в собственность жильем.
При вступлении в ССП потребитель заключает договор с ССИ, где указываются параметры его тарифного плана (срок накопления, ставка по депозиту, и т. п.). Кроме того, специальным решением государство обязуется выплачивать ему премию на сбережения из федерального или регионального бюджета. Участник, нарушивший контракт, получает накопленные деньги плюс определенный процент, но не получает премии. Если, однако, участник полностью выполнил программу накопления длительностью более определенного срока (обычно, более 5 лет), он вправе отказаться от кредита и получить все накопленные им средства с процентами и премией без покупки жилья. Таких агентов называют друзьями вкладчиков.
Ссудо-сберегательный институт (ССИ).
В рамках ССП процентные ставки по кредитам и депозитам меньше рыночных и обычно не зависят от инфляции. Небольшая маржа (разность между ставками, обычно 3%-4% ), а также процентный доход от инвестиций временно свободной кредитной массы являются источниками прибыли, получаемой ССИ. Однако прибыль ССИ определяется только в случае отсутствия кассовых разрывов.
Между администрацией и ССИ заключается соглашение о предоставлении вкладчикам бюджетных субсидий.
В рамках ЖНС проценты на сумму премий государства могут не начисляться.
Для выдачи кредитов формируется кредитная масса из целевых вкладов физических лиц, выплат в счет погашения ранее выданных кредитов, неиспользованного ранее остатка и резерва. Если денег для выплаты кредитов не хватает, то ССК формирует очередь вкладчиков за кредитом. В отличие от ССК банк для преодоления кассового разрыва должен привлечь собственные средства, поступившие от операций, не связанных с ССП, либо заемные средства. Средства ССП, временно свободные от обязательств перед вкладчиками и иными кредиторами, банк может использовать на вложения в государственные ценные бумаги или на иные рыночные операции.
Для покрытия финансовых разрывов ССИ может также создать специальный фондпо полнения распределяемой массы (резерв).Формирование резерва осуществляется за счет процентных доходов, полученных от вложений временно свободной части распределяемой массы в рыночные операции и государственные ценные бумаги.
Государство выплачивает вкладчику субсидии в процентах от его взносов (ежемесячно, ежеквартально, либо в конце каждого года).
3.Модель ССП (спецсчетов и стройсберкассы)
Проценты
В модели вводятся следующие ставки процента: ставка по депозитам - p, кредитная ставка - c, ставка по займу - z, ставка процента по внешним инвестициям - u, ставка начислений на сбережения (ставка субсидирования) - s. Если обозначить через pгод, cгод, uгод, zгод годовые ставки, то формулы перерасчёта на месяц следующие:
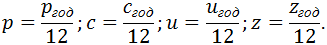
Время в модели дискретно. Единицей времени является месяц (в расчетах использовалась также квартальная модель). За один период времени производятся следующие операции. В начале периода вкладчики вносят деньги на депозиты. В конце периода им начисляются проценты и субсидии, кроме того заемщики осуществляют выплаты по кредитам. Затем внесённые агентами суммы и ранее накопленные средства используются для выдачи новых контрактных сумм.
Далее в тексте, если не оговорено иное, под значением функции в момент времени t понимается значение этой функции в конце периода t.
Для различения двух моделей будем использовать параметр δ.По определению
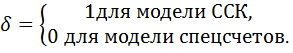
3.2. Накопление.
Будем считать, что социальные выплаты производятся каждый месяц: это упрощает формулы и вычисления.
Будем обозначать через A множество всех агентов–участников ССП (вкладчиков и заемщиков).
При появлении в системе агент a ∈ A задаётся тремя параметрами: временем появления в системе Tнач(a), размерамивзносов P(t,a) в месяц t и временем накопления τ(a). Для удобства записи формул там, где это несущественно, будем опускать параметр a. Каждый месяц в период накопления агент получает процент p на вклад. Кроме этого, каждый месяц агент получает социальные выплаты, то есть процент s от взносов P(t)за текущий месяц накопления.
Через Tкон(a) обозначим период последнего взноса агента a. Таким образом, Ткон = Тнач + τ - 1
Найдём объём накопления агента a. На момент времени t ≤ Tкон накопленная сумма М(t,a) в конце периода t вычисляется по формуле: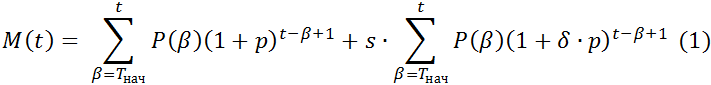
Мы считаем, что M(t) = 0, если верхний индекс суммирования меньше нижнего.
Правая часть этой формулы состоит из двух слагаемых: первое – взносы с учётом процентов, второе – социальные выплаты. Второе слагаемое отражает тот факт, что процент на социальные выплаты начисляется для ССК, но не для спецсчетов.
В случае t=Tкон получаем формулу для полного объёма накоплений:

3.3. Очередь
Если вкладчик ССК завершил накопление, но имеющийся в наличии объем кредитной массы недостаточен для выдачи ему контрактной суммы, то вкладчик попадает в очередь за кредитом. При этом он больше не делает взносов, и, хотя на накопленные им средства начисляется процент p, объём причитающегося ему кредита остаётся постоянным, поскольку зависит только от размера накоплений без учёта процентов, начисленных в очереди. Проценты влияют, однако, на объём контрактной суммы.
Итак, для данного агента a, стоящего в очереди в момент времени t ≥ Tкон, количество накопленных средств M(t) равно
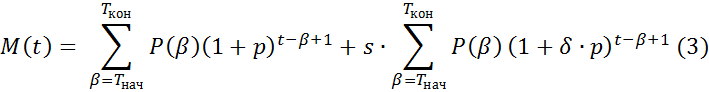
Объём контрактной суммы K(t,a) агента a в момент времени t ≥ Tкон равен сумме объёмов накопленных средств M(t,a) и кредита C(a). Считаем, что объем кредита пропорционален сумме M(Tкон); коэффициент пропорциональности Λ зависит от ССП
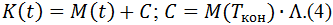
3.4. Кредитование.
Обозначим через Tкр(a) период, в конце которого агент a получает контрактную сумму. При отсутствии очереди Tкр(a) = Tкон(a). Первая выплата по кредиту производится в момент Tкр(a) + 1.
Введем характеристики кредита.
Срок кредита τкр(a) определяется временем накопления агента a (без учёта очереди), умноженного на коэффициент γ:
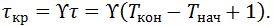
Процент за кредит обозначаем через c. Выплаты по кредиту рассчитываются по аннуитету. Это означает, что каждый периодагент выплачивает одну и ту же сумму денег, включающая выплату по телу кредита и проценты. Легко проверить, что ежемесячные выплаты B(a) по кредиту объемом C агента a вычисляются по формуле:
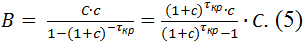
Tкр + 1 ≤ t ≤ Tкр + τкр (то есть, в момент t агент находится в состоянии выплат по кредиту). Через V(t,a) обозначим оставшийся объём тела кредита, а через E(t,a) - выплаты по телу кредита в момент времени t.
Формулы для вычисления V(t,a) и E(t,a) запишутся так (символ a опускаем):
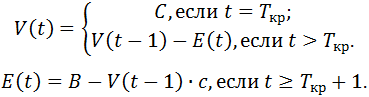
Найдём явное выражение для V(t) и E(t) через C. Учитывая (5), прямой подстановкой в определение несложно проверить, что
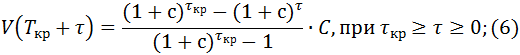
Отсюда получаем формулу для E(t) при t = Tкр + τ:
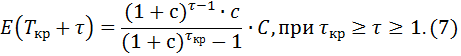
3.5. Друзья вкладчиков и нарушители контракта
Кроме обычных агентов, проходящих стадии накопления, очереди и кредитования, есть два особых типа агентов.
Друзья вкладчиков.
Этот тип агентов фактически выполняет вспомогательную функцию в ССП: они копят взносы, а затем отказываются от кредита, забирают свой вклад с процентами и субсидиями и выходят из системы. Друзьями могут быть только агенты, накапливающие 5 лет или более. За их счет поддерживается кредитная масса, обеспечивающая выплаты агентам-заемщикам.
В нашей модели количество друзей вкладчиков задается как доля от общего количества вкладчиков со временем накопления не менее 5 лет, начавших накапливать в данный момент.
Нарушители контракта
Это агенты, которые разрывают контракт на стадии накопления до ее завершения. Они забирают свои деньги с накопленными процентами, но без социальных выплат, и таким образом играют в модели роль, аналогичную друзьям вкладчиков. Будем характеризовать тип нарушителя сроком его пребывания в качестве вкладчика.
3.6. Ссудо-сберегательный институт (банк или ССК)
Несколько упрощенно схема работы ССИ выглядит так. В начале каждого периода мы собираем взносы от вкладчиков, и вместе с остатком средств за предыдущий период (если остаток положителен) инвестируем их под заданный процент. В конце периода полученные средства с процентами и выплаты по кредиту формируют так называемую кредитную массу. Далее выдаются средства друзьям вкладчиков и нарушителям. После этого обслуживаются агенты, ожидающие в очереди выдачи контрактных сумм. Как отмечалось выше, их место в очереди определяется некоторым правилом (в зависимости от момента завершения накопления, размера взносов, времени накопления); им последовательно выдаются контрактные суммы. В результате либо будут обслужены все агенты, ожидающие выдачи контрактных сумм, либо будет исчерпана кредитная масса. Остаток кредитной массы частично уходит в доход ССИ, частично переходит на следующий период.
Средства резерва, создаваемого ССК, отличаются повышенной ликвидностью. В нашей модели этот аспект не учитывается, мы считаем, что резервный фонд является частью остатка кредитной массы.
Будем говорить, что в момент времени t произошёл кассовый разрыв, если в этом периоде кредитной массы не хватает на обеспечение контрактами всех агентов, получивших право на кредит.
Отметим, что на начальной стадии существования системы не надо выдавать контрактные суммы агентам: они только накапливают средства. Поэтому на этой стадии не может быть кассового разрыва. В соответствующие периоды ССИ инвестирует имеющиеся у него средства, формируя кредитную массу, которая используется на начальных стадиях кредитования. Она пополняется благодаря притоку вкладчиков и выплатам по кредиту. Однако, когда в ССИ формируется «линейка» заемщиков, находящихся на разных стадиях выплаты кредита, накопленной кредитной массы и притока денег может оказаться недостаточно, тогда возникает кассовый разрыв. В этом случае ССК формирует очередь, а банк использует имеющиеся у него средства, либо прибегает к займу. В дальнейшем мы не различаем два последних способа покрытия разрыва банком, полагая, что стоимость для банка собственных и заемных средств одинакова. В обоих случаях привлечение средств сверх имеющейся кредитной массы рассматривается как заем.
В модели очередь и займы моделируются следующим образом. Назначается максимально возможное время нахождения в очереди Τ. Если в какой-то момент времени возникают вкладчики, находящиеся в очереди Τ периодов, то контрактная сумма выдаётся им за счёт займа. Каждый период заём пересчитывается с учетом новых займов или сокращения займа за счёт положительного остатка кредитной массы. Если Τ достаточно велико, то при естественных условиях займы отсутствуют; так моделируется ССК. Если Τ = 0, то очереди не возникает никогда. Так происходит, если в качестве ССИ выступает банк. На внешний заём начисляются процент z, заём с процентами выплачивается за счет кредитной массы.
Опишем еще раз временную последовательность действий ссудо-сберегательного института. В начале каждого периода рассчитывается объем взносов от вкладчиков; взносы используются для внешних инвестиций. Далее, рассчитывая объёмы накоплений M(t), контрактных сумм K(t) и выплат по кредитам B для всех агентов, которые находятся в системе на соответствующих стадиях, оцениваем кредитную массу. Выдаются деньги друзьям вкладчиков и агентам-нарушителям. Далее выдаются контрактные суммы, пока не исчерпается кредитная масса. Если в этот момент остались вкладчики, ожидающие в очереди Τ периодов, то ССИ выдает им контрактные суммы, используя заём. Остаток кредитной массы переходит на следующий период, и, если он положителен, то используется для инвестиций. Если же он отрицателен, то мы берём внешний заём и выплачиваем проценты по нему.
Будем обозначать через Δ(t) объём кредитной массы перед началом выдачи средств друзьям вкладчиков и агентам-нарушителям, Δкон(t) - остаток кредитной массы предыдущего периода.
3.4. Формирование и использование кредитной массы.
Во множестве агентов A выделим следующие подмножества: F(t) - друзья вкладчиков, заканчивающие накопления в момент t, R(T) - агенты-нарушители, разрывающие контракт в момент t, N(t) – агенты, находящиеся на стадии накопления в момент t, O(t) – агенты, ожидающие выдачи кредита в момент t, W(t) – агенты, выплачивающие кредит в момент t.
Формирование кредитной массы.
В начале периода t вкладчики приносят средства в размере 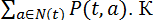 . К концу периода доход от инвестирования этих средств составит
. К концу периода доход от инвестирования этих средств составит 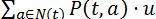 , где – ставка по внешним инвестициям, которую мы считаем фиксированной.
, где – ставка по внешним инвестициям, которую мы считаем фиксированной.
Кредитная масса в конце периода формируется следующим образом. От вкладчика a в неё поступает взнос P(t,a) с учётом инвестиций u и социальных выплат s, то есть P(t,a)(1 + u + s). От заёмщика приходит выплата по кредиту B(a).
Кроме этого, в кредитную массу включается остаток предыдущего периода Δкон(t-1) с учётом процентов. Если остаток был положителен, то в течение периода он использовался в качестве внешних инвестиций, если отрицателен, то для его покрытия был использован внешний заём, а значит, на него начислены проценты по займу. Считаем, что заем берется на один период, так что в конце периода он возвращается за счет имеющихся средств или нового займа. Для удобства записи введем обозначения Δкон+(t-1) = max{0,Δкон(t-1)}, Δкон-(t-1) = min{0,Δкон(t-1)}. Тогда в кредитную массу добавляется
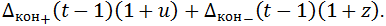
В итоге получаем, что объем кредитной массы Δ(t) до выдачи денег специальным агентам и контрактных сумм равен

Естественно считать, что z ≥ u, в противном случае можно было бы получать прибыль, просто инвестируя заимствованные средства. При выполнении этого естественного неравенства соотношение (8) можно переписать в более удобном виде
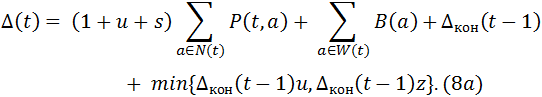
Величина остатка Δкон(t-1) задается указанной ниже формулой (11).
Выдача денег специальным агентам
Друзьям вкладчиков выдаются суммы M(t,a), накопленные ими к концу периода t. Агентам-нарушителям, прекращающим участие в ССП в момент t, выдаётся размер накопленной суммы за вычетом социальных выплат:
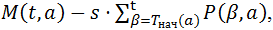
Таким образом, из кредитной массы вычитаются деньги на выдачу друзьям вкладчиков, агентам-нарушителям и возврат в бюджет. Обозначим кредитную массу после выдачи денег специальным агентам через 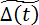 . Имеем:
. Имеем:
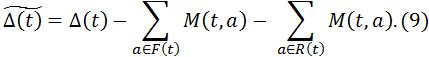
Отметим, что кредитная масса может оказаться отрицательной. Это означает, что мы берем заём на недостающую сумму.
Выдача контрактных сумм.
ССИ должен выдать кредиты агентам, которые закончили накапливать средства. Выдача происходит следующим образом: агенты выстраиваются в некотором порядке, а потом им по очереди выдаются денежные средства. Порядок может быть устроен разными способами и учитывать время нахождения в очереди, размер ежемесячного взноса, время накопительного периода. Можно, например, упорядочивать агентов, прежде всего, по убыванию времени ожидания в очереди, потом - по убыванию времени накопления и затем по убыванию ежемесячных взносов. Если при этом все же возникает неоднозначность, то можно дополнительно использовать случайный выбор.
Обозначим через H- упорядоченный список агентов, которым нужно выдать контрактные суммы K(t,Hi) (объём контрактных сумм определяется формулой (4)), здесь Hi-i-ый агент в очереди. Находим максимальное число вкладчиков m ,которым можно выдать контрактную сумму, не используя заём. Оно определяется формулой:
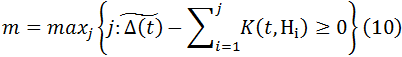
Выдаем контрактные суммы всем агентам H1, H2, ..., Hm. Если после этой операции остались агенты, которым надо выдать контрактную сумму за счёт займа (это агенты, которые стоят в очереди ровно Τ периодов), то им тоже выдаём контрактную сумму. Пусть l- последний номер агента, который находится в очереди Τ периодов (если таких нет, положим l = 0). Тогда множество агентов, которым выдаются контрактные суммы, запишется так: {Hi|i = 1, ... , max (m,l)}. Таким образом, обозначив через Δкон(t) оставшуюся после выдачи контрактных сумм кредитную массу, имеем с учетом (4):
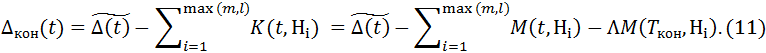
Остаток кредитной массы Δкон(t) переходит на следующий период. Операционные издержки банка, равно как издержки на резервирование и страхование мы не учитываем.
Соотношения (1)-(11) вместе с(не конкретизированными выше) правилами формирования очереди описывают динамикуссудо-сберегательной программы.
4. Устойчивость ссудо-сберегательных программ
Напомним введенные выше основные понятия. Под ссудо-сберегательной программой мы понимаем совокупность правил сбережения, назначения премии, формирования очереди за кредит, предоставления займов, выбора момента выдачи кредита, определения его объема, срока и объёмов выплат. Тарифным планом будем называть набор числовых характеристик ССП.
Каждый агент ССП может в произвольный момент времени находиться в состоянии вкладчика, очередника и заемщика. Вкладчик характеризуется временем пребывания в ССП и функцией, определяющей размер взноса в каждый момент времени; кроме того, он может быть нарушителем, выходящим из системы в тот или иной момент времени, или другом вкладчиков. Очередник характеризуется текущим объемом накоплений, объемом, накопленным за период накопления, и временем пребывания в очереди. Заемщик характеризуется временем с момента получения займа, объемом невыплаченного кредита и программой выплат. Перечень агентов со всеми их характеристиками определяет состояние тарифного плана (режим) ССП. Упорядоченная по времени последовательность состояний ССП называется ссудо-сберегательной траекторией (кратко – просто траекторией, или ССТ).
Теперь определим прибыль ССП. Логично предположить, что ССП не получает никакой прибыли в момент времени t, если остаток кредитной массы Δкон(t) отрицателен (то есть, если мы находимся в состоянии кассового разрыва). Вместе с тем, если для данной траектории остаток, начиная с некоторого момента времени постоянно растёт (то есть, если постоянно образуются средства, не используемые для выдачи контрактных сумм и покрытия прочих затрат), то можно забирать некоторую часть остатка в прибыль ССП. Будем считать, что при такой возможности, в прибыль отчисляется максимально возможная сумма средств. Дадим формальное определение:
Прибылью Ω(t0) в момент времени t0 называется такое максимальное значение X,0 ≤ X ≤ Δкон(t0), что при замене остатка Δкон(t0) на Δкон(t0) - X изменённая ССТ не будет находиться в состоянии кассового разрыва в моменты времени t ≥ t0.
Прибыль определена только для тех ССТ, у которых с некоторого момента времени t0 не возникает кассовых разрывов, или, что то же самое, Δкон(t) ≥ 0 при t ≥ t0. Такие ССТ будем называть финансово устойчивыми.
Замечание. При нашем определении прибыли мы должны знать, как будет вести себя траектория в будущие моменты времени. На практике мы не знаем будущие параметры и должны исходить из их прогноза, обеспечивая отсутствие разрывов с некоторой вероятностью.
Будем говорить, что ССТ финансово устойчива в сильном смысле, если она не допускает финансовых разрывов вовсе, т.е. Δкон(t) ≥ 0 при всех t ≥ 0. Сильно устойчивая ССТ не предусматривает ни очередей, ни займов.
Соответственно, СПП финансово устойчива (в сильном смысле), в заданной области экзогенных параметров, если для любого набора из этой области устойчива (сильно устойчива) любая порожденная ею траектория.
Когорты и потоки когорт
Назовём двух агентов a, b ∈ A одинаковыми, если у них совпадают все характеристики накопления, именно момент начала накопления, его срок и объем ежемесячных вкладов: 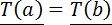 ,
, 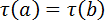 ,
, 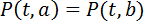 для всех t. Совокупность всех одинаковых агентов назовем когортой
для всех t. Совокупность всех одинаковых агентов назовем когортой
Назовем двух агентов a, b ∈ A подобными, если у них совпадают сроки накопления и объемы ежемесячных вкладов: τ(a) = τ(b), P(t,a) = P(t,b) для всех t. Совокупность всех подобных агентов назовём потоком когорт. Ясно, что поток когорт разбивается на когорты по времени появления в системе. Будем считать, что характеристики потока когорт – срок и объем ежемесячных вкладов - однозначно определяют долю в ней друзей вкладчиков, а также долю и временную структуру нарушителей контракта.
Таким образом, совокупность вкладчиков, прибывающих в каждый момент времени, можно разбить на когорты. Если это разбиение не зависит от времени, мы говорим, что приток вкладчиков стационарен.
Стационарный приток естественным образом порождает стационарную (не зависящую от времени) структуру потоков когорт, по крайней мере, до начала кредитования. В отсутствии кассовых разрывов структура остается стационарной всегда. Стационарность может нарушаться, если в число характеристик агентов включить время ожидания в очереди, а также факт пребывания в состоянии заемщика. В этом случае возможно «распадение» когорт: в некоторый момент времени часть когорты, получившей право на кредит, может реализовать его, а другая часть - находиться в очереди.
Будем обозначать через Aα поток когорт α, а через Aα,Тнач – когорту агентов из потока когорт Aα, которые вступают в систему в момент времени Тнач. Для агентов потока Aα через τ(α) обозначим время накопления для агентов данного потока, через P(α) – взнос агента из потока когорт α, M(Tнач + i,α) - суммарное накопления агента из α через i периодов после начала накопления. Так как объёмы кредитов зависят только от размеров накоплений за τ(α) периодов, они одинаковы для всех членов когорты. Объём кредита обозначим через C(α). При стационарном притоке, если нарушители и друзья вкладчиков отсутствуют, то число членов каждой когорты не меняется: |Aα,t0| = |Aα,t1| для любых t0, t1.
Через L(α) обозначим начальное число вкладчиков в когорте α, а через N - суммарный приток вкладчиков по всем когортам: N = ∑αL(α).
Назовем ССТ стационарной, если она финансово устойчива и, начиная с некоторого момента времени, стационарна структура потоков когорт, находящихся на каждой стадии накопления, ожидания и кредитования. Если при этом взносы агентов на разных стадиях накопления и платежи по кредиту на разных стадиях выплат по кредиту не зависят от времени, то ССТ называется однородной.
Исследуем, как будет вести себя ССП при заданном начальном наборе параметров. Будем рассматривать допустимые траектории. Нас интересует, будет ли программа финансово устойчивой или даже сильно устойчивой. Всюду в дальнейших теоретических рассмотрениях предполагается, что приток вкладчиков стационарен. В этом случае величина накопления M(Tнач + i,α) не зависит от Tнач, значит, M(Tнач + i,α) = M(i,α). Это обозначение используется в дальнейшем.
Естественная и важная задача - исследовать ССП на устойчивость. Для этого надо подсчитать кредитную массу, сформировавшуюся в период накопления с учетом процентов, рассмотреть ее эволюцию в процессе формирования линейки заемщиков и исследовать условия отсутствия разрывов. Задача сводится к исследованию траекторий, задаваемых соотношениями (8) - (11).
4.1. Условия финансовой устойчивости.
При исследовании устойчивости ССП будет рассматриваться упрощенный вариант модели. Считаем, что нарушители контракта отсутствуют, а при нехватке кредитной массы очередь не формируется, а используется внешний кредит. Кроме того, предполагаем, что процент по инвестициям не превосходит процента по внешнему кредиту: z ≥ u. Предположим также, что на входе имеется лишь один поток когорт. Так как начисления, кредитная масса, объёмы контрактной суммы и кредита пропорциональны взносу агента, будем считать, что в каждой когорте есть один агент и d друзей вкладчиков (d–доля от 0 до 1), взносы постоянны и равны 1.
Для упрощения формул введем обозначения:
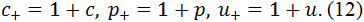
Кредитная масса Δ(τ) вычисляется по следующей формуле:
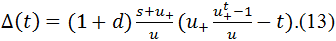
Для доказательства этой формулы нужно аккуратно выписать рекуррентные соотношение на кредитную массу (формулу (8)) и многократно её применить.
По определению, для сильной финансовой устойчивости необходимо и достаточно выполнение неравенства Δкон(t) ≥ 0 для всех t. Из формулы (13) следует, что Δкон(t) ≥ 0 при t < τ. Найдём выражение для Δкон(t) при t ≥ τ.
Начиная с момента времени τ, мы выдаём контрактные суммы и возвращаем средства друзьям вкладчиков. Так как нет очередей, то каждый период выдаётся ровно одна контрактная сумма. Величина ее равна M(τ)(1 + Λ) (см. (4)), где объем накоплений M(τ) равен
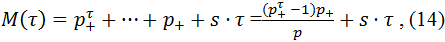
Поскольку специальные агенты и очередь отсутствуют,
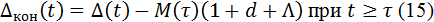
При z ≥ u согласно (8а) имеем
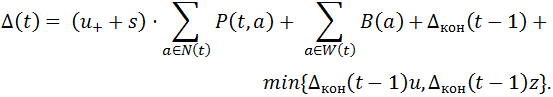
В нашем случае взнос вкладчика P(t,a) = 1, взносы друга вкладчика равны d; число агентов на стадии накопления равно сроку накопления τ, умноженному на коэффициент (1 + d); число агентов, выплачивающих кредит равно min{τкр,t-τ}. Из этих соотношений и (14) получаем
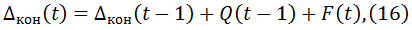
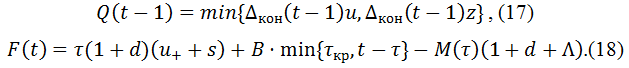

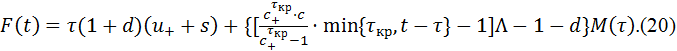
Уравнение (16) вместе с соотношениями (14), (17), (20) задает ссудо-сберегательную траекторию. Исследуя её свойства, мы получаем следующую теорему, описывающую финансовую устойчивость ССТ.
Теорема 1.
Для финансовой устойчивости ссудо-сберегательной траектории необходимо выполнение неравенства
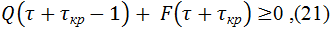

В случае Δкон(τ + τкр - 1) ≥ 0 условие (21) является необходимым и достаточным, а в случае Δкон(τ + τкр - 1) < 0 этим свойством обладает условие (22).
Поскольку z ≥ u, непосредственно из Теоремы 1 получаем следующее утверждение.
Следствие 1.
В случае Δкон(τ+τкр-1)≥0 условие
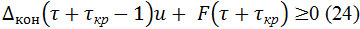
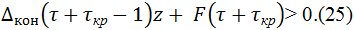
Следствие 2.
В случае F(τ+τкр) ≤ 0 условие (24) необходимо и достаточно для финансовой устойчивости, а в случае F(τ+τкр) > 0 этим свойством обладает условие(25).
Нижеследующие утверждения полезны для понимания структуры финансово устойчивых ССТ.
Утверждение 1. Пусть ССТ финансово устойчива, но не сильно финансово устойчива. ТогдаF(τ+τкр)>0
Утверждение 2. Пусть ССТ финансово устойчива, но не сильно финансово устойчива. Тогда найдется период t0 такой, что τ ≤ t0 < τ + τкр, F(t0) < 0.
Полученная картина ССТ вполне соответствует экономической интуиции. После начала выдачи кредитов величина чистого притока Q(t-1)+F(t) может оказаться отрицательной; при этом запас средств, накопленный за начальные периоды, постепенно уменьшается. Но F(t) растёт за счет выплат по кредитам. Возможно, что мы не исчерпаем запас Δкон до того, как величина F стнает положительной; в этом случае ССТ сильно устойчива. В противном случае приходится брать внешний заём. Если F(t) вырастет настолько, что величина Q(t-1)+F(t) станет положительной, то Δкон также начнет расти и в конце концов обретет положительный знак. Тогда ССТ финансово устойчива. Если же Q(t-1)+F(t) остается отрицательной, то устойчивость не имеет места.
4.2. Условия сильной финансовой устойчивости.
При сильной финансовой устойчивости ССТ уравнение (16) запишется так:
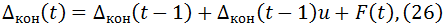
Многократно применяя (26), (18) и используя (19), получаем, что при t ≤ τкр + τ выполнена следующая формула:
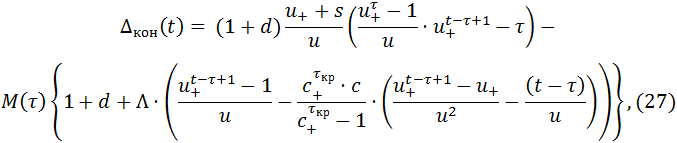
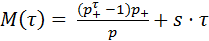 .
.Начиная с момента времени t = τкр + τ, F(t) не меняется. Значит, при t ≥ τкр + τ остаток кредитной массы вычисляется по формуле:
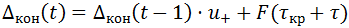
Снова используя неубывание функции F(t) по t, получаем необходимое и достаточное условие сильной финансовой устойчивости.
Утверждение 3. Пусть t0 ≥ τ - минимальное число такое, что выполняется неравенство F(t0) ≥ 0. ССТ сильно финансово устойчива тогда и только тогда, когда Δкон(t0-1) ≥ 0.
Суммируем наши выводы.
Теорема 3. Пусть ? t0 – минимальное число такое, что t0≥τ и
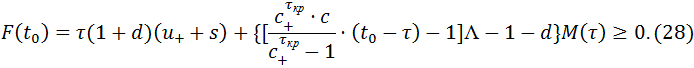
Для сильной финансовой устойчивости одного потока когорт с параметрами p,u,s,c,τ,τкр,Λ необходимо и достаточно выполнения неравенства:
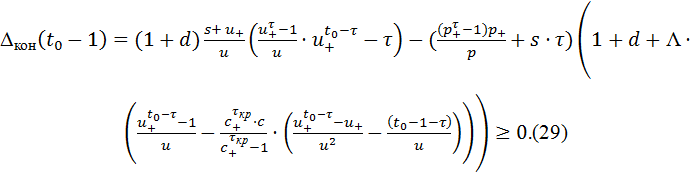
Заметим, что сильная устойчивость однородной ССП (представляющей собой набор потоков когорт с неизменными во времени параметрами) заведомо обеспечивается сильной устойчивостью каждого потока.
Следующее утверждение показывает, что некоторых разумных ограничениях на параметры, величина F(τкр+τ) будет неотрицательной,так что (28) выполняется.
Утверждение 4. Если
Как следует из доказательства, в условиях Утверждения 4 неравенство F(τкр+τ)≥0 выполняется и при Λ&kt;1 , если Λ не слишком мало.
5. Экспериментальное исследование ссудо-сберегательных траекторий
5.1. Базовый тарифный план
Задача экспериментального исследования состояла в изучении устойчивости тарифного плана, близкого к реально используемому в рамках «Народной ипотеки», при варьировании внутренних и внешних параметров. В базовом примере ежемесячный взнос вкладчиков был принят равным 10тыс. рублей, срок накопления 5 лет; процентная ставка по вкладу 2%; начисление ежемесячное; срок кредита в полтора раза больше срока накопления; процентная ставка по кредиту 6%, начисление ежемесячное; размер кредита равен 100% от суммы накоплений на вкладе. Социальная выплата равнялась 30% от суммы денежных средств, внесенных участником на вклад за календарный месяц. На социальные выплаты проценты по депозиту не начислялись. Предполагаем, что доля «друзей вкладчиков» (отказывающихся от кредита после завершения 5 и 6 лет накопления) составляет 20% от численности когорты. Процент на внешнем рынке равен 8% годовых. Очереди и досрочные расторжения договоров отсутствуют. Не учитываются также дефолты по кредитам.
Полная линейка заёмщиков формируется через 12,5 лет (5 лет накопления и 7,5 лет выплаты кредита). Поэтому расчёты разумно ограничить 18 годами (точнее, в модели рассматривалось 200 периодов времени) – в этот период полная линейка заёмщиков уже функционирует некоторое время и процесс стабилизирован.
На рис. 1 показан остаток кредитной массы при заданных параметрах. Первые 5 лет остаток растёт (мы не выдаём контрактные суммы, а только накапливаем денежные средства). Далее, приблизительно до 10-го года остаток уменьшается за счёт выдачи кредитов. Выплаты по кредиту постепенно растут, и, начиная с 130-го месяца, остаток снова увеличивается. Таким образом, при данных параметрах наблюдается сильная финансовая устойчивость.
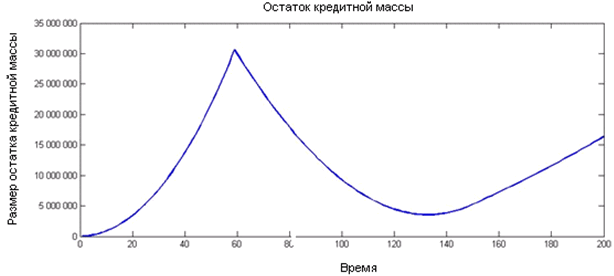
Рис. 1. Динамика остатка кредитной массы в условиях базового примера.
Оценим теперь размер прибыли ССП в базовом примере. В принципе, можно изымать весь остаток кредитной массы, начиная с момента, когда выплаты по кредитам становятся достаточно большими (минимум графика на рис.1, это 135-й период времени). Однако на практике этот способ неудобен, он требует точного прогноза всей траектории.
Более практичным выглядит правило, в соответствии с которым в каждый момент времени изымается фиксированный процент средств из остатка. Естественно использовать такую ставку процента, при которой сохраняется сильная финансовая устойчивость.
В результате расчётов получаем, что максимальная допустимая ставка равна 1,8%. Удобно рассматривать относительный объём прибыли, то есть отношение прибыли к объему депозитов в данный момент времени. График относительного объёма прибыли за период изображен на рис. 2.
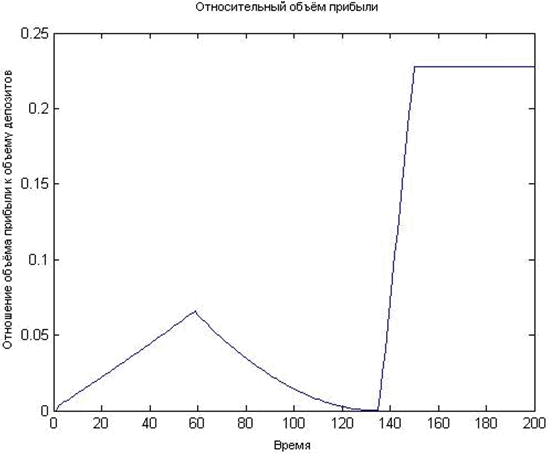
Рис. 2. Относительный объем прибыли.
Поведение объёма прибыли соответствует поведению кредитной массы до периода 135 (11 лет с начала работы системы). В 136-й период величина F(t) становится положительной, и прибыль пропорциональна остатку кредитной массы. Начиная с периода 150 (12,5 лет работы системы) становится постоянной (сформирована полная линейка заёмщиков).
5.2. Границы устойчивости и прибыльности: варьирование параметров тарифного плана.
Исследуем, как изменятся объёмы и максимальный процент прибыли при изменении следующих параметров: доли друзей вкладчиков, отношения объёма кредита к объёму накопления, отношения срока кредитования к сроку накопления и ставок процента на государственные субсидии, на инвестиции, на кредиты и на накопления.
Под отношением объёмом прибыли к объему депозитов мы будем подразумевать отношение суммарного объёма прибыли к суммарному объему депозитов в момент времени 200.
Изменение доли «друзей» вкладчиков d.
Определенная доля вкладчиков, которые отказываются от кредита и чьи средства служат источником финансирования долгосрочных кредитов, жизненно необходима для стабильной работы ССП. На рис. 3 показано, как изменяются параметры прибыли при изменении доли друзей d.
При доле друзей d=0,1 сильная финансовая устойчивость нарушается, но ССП остается финансово устойчивой даже при отсутствии друзей вкладчиков. По мере роста количества друзей растет и прибыль.
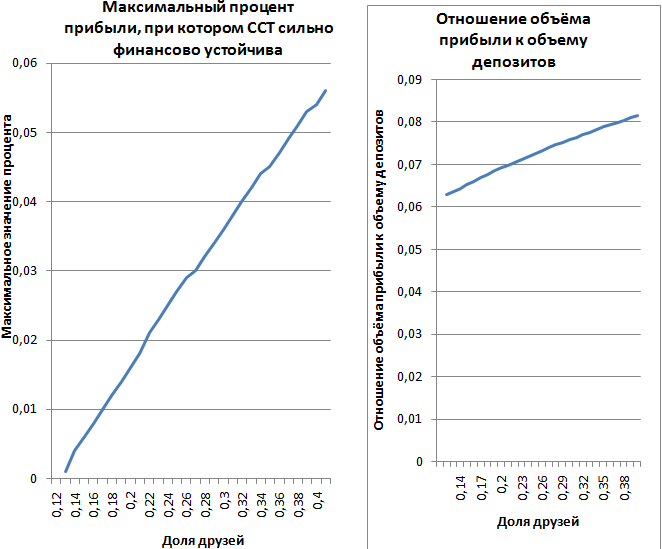
Рис. 3.Прибыль при изменении доли друзей вкладчиков.
Изменение объема кредита Λ.
Объем кредита определяется как доля Λ от объема накоплений. На рис. 4 показано, как влияет изменение этой доли на прибыль.
Как и следовало ожидать, увеличение?приводит к уменьшениюприбыли. Граница сильной финансовой устойчивости достигается при Λ = 1.1, а граница финансовой устойчивости - при Λ = 3,5. Отметим, что относительно небольшие изменения этого параметра довольно сильно влияют на объём и допустимый процент прибыли.

Рис. 4. Прибыль при изменении отношения объема кредита к объёму накопления.
Срок кредитования.
Напомним, что в базовом примере срок кредита равен 150% от срока вклада. Увеличение срока кредита приводит к уменьшению прибыли. Граница сильной финансовой устойчивости достигается при отношении срока кредитования к сроку накопления), равном 1.7, а граница финансовой устойчивости - при отношении, равном 5.
Изменение процентных ставок: субсидий на сбережения, инвестиционного дохода, ставки по внешнему кредиту. Для всех трех параметров наблюдается похожая динамика: максимальный процент и объём прибыли увеличиваются при увеличении ставки, при этом система реагирует слабее, чем на изменение рассмотренных выше параметров. Реакция на изменение доходности инвестиций отражена на рис. 5.

Рис. 5. Прибыль при изменении процента на инвестиции
Для процента по субсидиям сильная финансовая устойчивость наблюдается даже при 0%. Для процента по кредиту граница сильной финансовой устойчивости достигается при 3,9%, а финансовой устойчивости при 1,5%.
Изменение процента на накопления.
Проследим за изменением процента на накопления. Динамика приведена на рис. 9. При увеличении процента прибыль падает. Граница сильной финансовой устойчивости достигается при значении 3,6%, финансовой устойчивости при 7,5%. Как и остальные проценты, изменение этого параметра оказывает более слабое влияние, чем изменение размера кредита или времени кредитования.
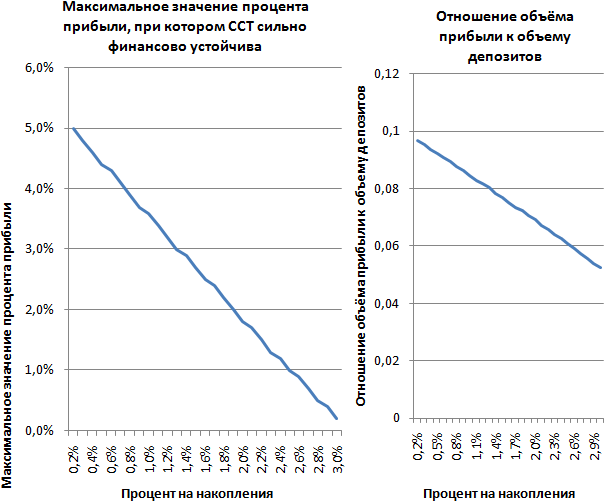
Рис. 6. Изменения процента на накопления.
Падение притока вкладчиков.
Устойчивость к изменению притока вкладчиков – важнейшее свойство ссудо-сберегательных траектории. В данной модели была проведена серия соответствующих расчетов. А именно, в описанном выше базовом примере для данных параметрах рассматривались ситуации падения притока на величину 1-λ, 0≤λ<1 в разные моменты времени t после падения приток вкладчиков оставался неизменным. Таким образом, значение λ=0,5 соответствовало падению притока вкладчиков на 50%, а λ=0 - полному падению притока.
В результате эксперимента оказалось, что даже полное прекращение притока в моменты времени t>170 не нарушает сильную финансовую устойчивость. На рис. 7 показано, как изменяется количество периодов использования внешнего займа в зависимости от t и λ.
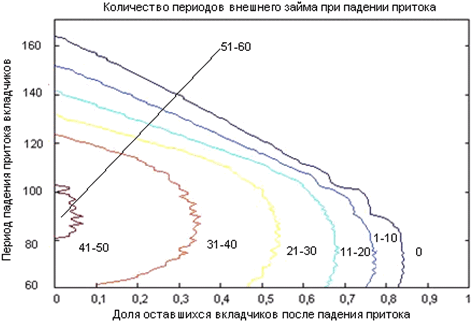
Рис. 7. Количество периодов внешнего займа при падении притока вкладчиков.
Естественно считать, что t≥60, когда уже есть агенты, выплачивающие кредит. На рис.7 представлены линии уровня, соответствующие числам периодов внешнего займа 0;10; 20;30;40;50. Как видно, небольшое падение доли вкладчиков (до 0,17 от начального количества) не влияет на сильную финансовую устойчивость независимо от момента шока. При более значительном падение всё зависит от того, в какой период времени оно происходит. Если момент шока достаточно удален от начала функционирования системы, то падение притока слабо влияет на количество периодов внешнего займа (уже выдано достаточно кредитов, чтобы поддерживать систему). При выбранных параметрах самый плохой сценарий развивается при падении притока в 89-й период. К этому моменту уже выдано много кредитов, кредитная масса не очень велика, а функция F(t) ещё отрицательная, поэтому изменение притока вкладчиков неблагоприятным образом влияет на устойчивость ССТ.
6. Заключение
Предложенная в работе динамическая модель ссудо-сберегательной программы предназначена для исследования, оценки и выбора параметров накопления, кредитования и субсидирования участников ипотечных институтов, где режим кредитования вкладчиков зависит от параметров выполненной вкладчиком программы накопления средств.
Модель может быть востребована тремя группами пользователей:
- непосредственно стройсберкассами и банками для разработки планов накопления и кредитования;
- Министерством финансов для разработки и анализа правил начисления премий вкладчикам на накопления;
- надзорным органом (Центральным банком) для анализа и утверждения тарифных планов, предлагаемых стройсберкассами и банками населению, и разработки нормативов финансовой устойчивости стройсберкасс.
Кроме того, модель может быть использована для научных исследований системы ССП и выработки предложений по ее совершенствованию.
Полученные выше теоретические результаты и компьютерные расчеты, показали, что в российских условиях существуют ССП, которые обеспечивают устойчивую работу ссудо-сберегательных счетов в широком диапазоне изменения внешних условий и параметров. Отметим, что при разработке так называемой «Народной ипотеки»– системы спецсчетов, реализованной в Краснодарском крае (см., например, Михайлова, 2013),была использована модель, близкая к описанной выше.
Имеется ряд перспективных и важных как в теоретическом, так и в прикладном аспекте, направлений дальнейшего развития предложенного подхода, а именно:
- учет связи между параметрами ССП и притоком вкладчиков; в частности, важно исследовать, в какой мере на приток влияют размер премии на сбережения и длительность ожидания в очереди при тех или иных внешних условиях;
- исследование эффективности различных мер по предотвращению опасности «бегства вкладчиков» (своевременное использование резервного фонда, увеличение премии на сбережения, смена тарифного плана).
- учет возможности совмещения различных тарифных планов;
- исследование правил расчета рейтинга вкладчиков при формировании очереди;
- составление методических рекомендаций по разработке и анализу тарифных планов ССП; разработка нормативных показателей для контроля ССП;
- учет в модели функций полезности участников информирования их спроса на услуги ССП с целью анализа эффективности ССП как ипотечного института на разных стадиях развития экономики.
- разработка принципов постепенного преобразования ССП в банковский институт (по мере исчерпания функций ССП) путем сокращения премии на сбережения, увеличения процентных ставок и расширения допустимых направлений деятельности ССП.
Доработка модели в соответствии с 1)-4) существенно улучшит ее качество как инструмента анализа и контроля. Выполнение пункта 5) позволит существенно сократить издержки по внедрению ССП; разработанные рекомендации могли бы непосредственно использоваться на практике. Исследование проблемы 7) позволило бы сформировать рациональную государственную политику в отношении ССП на период 15-25 лет.
Можно ожидать, что в скором времени в России будет создано несколько десятков ссудо-сберегательных программ. Каждая стройсберкасса и каждый банк, предлагающий вкладчикам спецсчета, сможет вести систематические расчеты по модели с учетом меняющихся условий – темпов инфляции и доходов населения, объема премий на сбережения, притока новых вкладчиков и т.п. Аналогичный пересчет должен будет осуществляться регулирующими органами.
Литература
- Ильинский Д.Г., В. М. Полтерович, О.Ю. Старков (2012).Моделирование накопительных жилищных счетов в г. Краснодаре. Отчет о научно-исследовательской работе. Договор № 12/01 о проведении научно-исследовательской работы для ОАО «Агентство развития Краснодарского края». Выполнено под рук. В.М. Полтеровича. М.: Новая экономическая ассоциация.
- Полтерович В.М., Старков О.Ю. (2007). Формирование ипотеки в догоняющих экономиках: проблема трансплантации институтов. М.: Наука. – 196 с.
- Полтерович В.М., Старков О.Ю. (2010). Поэтапное формирование массовой ипотеки и рынка жилья. В кн.: Полтерович В.М. (отв. ред.) Стратегия модернизации российской экономики// СПб.: Алетейа.
- Полтерович В.М., Старков О.Ю. (2011). Проектирование выхода из институциональной ловушки (на примере ипотеки в России).
- Михайлова Д.(2013). Народная ипотека набирает обороты. Bankir.ru. 22.06.2013.
«Народная ипотека» на Дону принесла первые плоды (2013). Ростов-дом. - Laux H. (2005). Die Buasparfinanzierung. Die finanziellen Aspekte des Bausparvertrages als Spar- und Kreditinstrument. 7 Auflage. FrankfurtamMain: VerlagRecht and Wirtschaft GmbH.
- ScholtenU. (2000).Rotating Savings and Credit Associations in Developed Countries: The German–Austrian Bausparkassen// Journal of Comparative Economics. № 28.


































Написать комментарий
Полтерович и примкнувшие к нему пытаются систему кредитования перелицевать в систему МММ. Полтерович что-то вроде Мавроди.Тот ведь тоже математик. Но зайцы всё равно не пропадут. Они родились под кустом, под кустом их и убьёт охотник. А куст перейдёт по наследству другому зайцу. Зачем зайцу ипотека? Зайцы не клиенты ни Мавроди, у них нет денег, ни Полтеровича, у них как у стрекозы под каждым кустом и стол и дом.
Так и не понял Где же будут жить зайцы
М-м-м-дя-а-а. Не дано пифагорейцам людей понять, не дано...