Что такое «технологическая сингулярность» и «технологическая дыра» в уравнении Полтеровича–Хенкина? В чем состоит теория Полтеровича–Тониса о переключении режима заимствования технологий на режим их создания? Как теория технологических ловушек описывает микроэкономический механизм технологической диффузии?
Одним из ключевых вопросов экономической теории является понимание механизмов рождения и распространения инноваций. Более того, по мнению многих аналитиков, именно эти два механизма лежат в основе доминирования Западной цивилизации. Без интенсивного рождения инноваций Западный мир не смог бы обогнать Восток в лице Китая и Индии [11], но без бурного накопления капитала и инвестирования в распространение новых технологий Запад не смог бы обеспечить своего тотального превосходства [12]. Таким образом, вопрос о механизмах рождения и распространения инноваций имеет цивилизационное звучание, чем и определяется его актуальность.
В настоящее время в данной области накоплен большой арсенал работ, в которых рассматриваются различные аспекты инновационных процессов. Однако в данной статье нас будут интересовать специфические вопросы, некоторые из которых до сих пор не нашли содержательного толкования и обсуждения, а некоторые – были раскрыты лишь совсем недавно. Вместе с тем уяснение закономерностей рождения и распространения технологических инноваций позволяет объяснить широкий спектр экономических явлений.
1. Традиционная логистическая модель
Наиболее типичным в исследованиях инноваций является рассмотрение процесса их распространения. На этом аспекте мы остановимся более подробно.
К агрегированным моделям инновационного рынка будем относить модели, которые изучают поведенческие свойства больших сегментов экономики. Как правило, экономические интересы отдельных хозяйственных структур в таких моделях не учитываются, а потому модели такого рода являются преимущественно дескриптивными. Одной из основополагающих моделей инноваций является диффузионная модель их распространения. В соответствии с ней распространение нововведения зависит как от числа фирм, уже внедривших инновацию, так и от числа фирм, еще не освоивших ее. В каноническом виде данная модель представляется в форме следующего диффузионного дифференциального уравнения:

Решением уравнения (1) является так называемая логистическая функция вида [1]:

Данная кривая имеет S–образную форму и хорошо отражает специфику инновационных рынков, а именно: первоначальный бурный рост с последующим насыщением рынка и его стабилизацией. Данная динамическая закономерность развития инновационного рынка по полному праву может считаться основной.
Модель (1) имеет огромное значение для изучения инновационного рынка. Во-первых, она имеет вполне приемлемую теоретическую основу, опираясь на правдоподобную гипотезу. Во-вторых, все параметры модели для конкретных ситуаций довольно легко идентифицировать и интерпретировать. В-третьих, логистическая зависимость подтверждается эмпирическими исследованиями и является широко применимой на практике.
Надо отметить, что модель (1) служит на самом деле некоей базовой конструкцией, так как в отдельных исследованиях фигурирует огромное число ее модификаций [1]. Тем не менее, даже существующие модификации модели (1) так или иначе выходят на интегральные кривые, по своей форме напоминающие логисту.
Следует сказать, что диффузионная модель (1) не относится к макроэкономическим моделям. Дело в том, что она по своей экономической сути воспроизводит некий переходный процесс в становлении нового рынка; она рассматривает определенный рынок (его сегмент) и его заполнение новым продуктом, хотя этот процесс может рассматриваться и на макроуровне.
В литературе принято различать два типа участников инновационного рынка: фирмы-инноваторы (лидеры, создающие инновации) и фирмы-имитаторы (те, кто заимствует уже появившуюся на рынке инновацию). Диффузионная модель (1) описывает поведение именно предприятий-имитаторов, в то время как процесс рождения инновации в ней не отражен. Между тем эти два процесса являются сопряженными и должны быть интегрированы в современные модели инновационных процессов.
2. Эволюционная модель диффузии технологий Полтеровича–Хенкина
Недостаточность диффузионной модели (1) для описания промышленных рынков связана с одним примечательным эмпирическим фактом. Дело в том, что как в экономике в целом, так и в отдельных отраслях сосуществуют разноэффективные технологии. Причем кривые распределения мощностей какой-либо отрасли (экономики) по уровням эффективности для разных моментов времени похожи друг на друга. Более того, наблюдается определенное сходство между данными кривыми для разных отраслей [2]. Тем самым можно говорить об универсальности «пространственной» кривой распределения технологий, о ее устойчивости (инвариантности) во времени.
Между тем указанный факт противоречит традиционным экономическим теориям, в соответствии с которыми вложения капитала должны осуществляться лишь в наиболее эффективные (прибыльные) технологии, а потому доля низкорентабельных производственных мощностей должна быть пренебрежимо малой или, по крайней мере, она должна уменьшаться во времени, как это и предполагает традиционная диффузионная модель. Для устранения этого противоречия В.М.Полтеровичем и Г.М.Хенкиным была предложена эволюционная модель взаимодействия процессов создания и заимствования технологий, которая позволила увязать два отмеченных факта – логистический характер диффузионных «временных» кривых распространения технологий и устойчивую форму «пространственных» кривых распределения производства (мощностей) по уровням эффективности – и показать, что они являются двумя сторонами единого механизма «динамического равновесия» между инновационными и имитационными процессами. Для этого авторы рассматривали следующее эволюционное уравнение [2]:
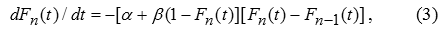
Уравнение (3) предполагает довольно прозрачную вероятностную трактовку. Скорость перехода изменения доли предприятий с технологическим уровнем, не большим n, раскладывается в правой части (3) на две составляющие: вероятность перехода предприятия с уровня n на следующий (n+1)-ый уровень за единицу времени в процессе инновации; вероятность перехода предприятия с уровня n на следующий (n+1)-ый уровень за единицу времени в процессе имитации. Этот процесс можно конкретизировать. Так, первое слагаемое
С математической точки зрения модель (3) представляет собой дифференциально-разностное уравнение, решением которого является следующая волновая функция [2]:

Несложно видеть, что функция (4) очень похожа на логистическую кривую (2), хотя в нее «примешивается» фактор технологических различий n. При фиксированном t функция (4) определяет так называемое логистическое распределение вероятностей, а при фиксированном n задает убывающую логистическую кривую, описывающую изменение во времени доли предприятий, находящихся на уровне эффективности n; изменение параметра А приводит к сдвигу распределения [2].
Более тщательный формальный анализ семейства функций (4) позволил установить факт экспоненциальной (то есть достаточно быстрой) сходимости распределения предприятий по уровню эффективности к логистической зависимости [2]. Иными словами, в результате взаимодействия инновационного и имитационного процессов с течением времени форма кривой распределения технологий по эффективности стабилизируется; ни форма, ни скорость в асимптотике не зависят от начальных условий и, следовательно, от отраслевой специфики инновации и фазы ее жизненного цикла. Таким образом, модель Полтеровича–Хенкина дает непротиворечивое объяснение двум наблюдаемым в реальности закономерностям функционирования инновационных рынков. Впоследствии модель (3) была обобщена для случая произвольного закона эволюции «пространственной» кривой технологий, хотя получить принципиально новые выводы это уже не позволило [3].
Модель Полтеровича–Хенкина имеет большое значение по двум причинам. Во-первых, она продемонстрировала, что в рамках одного уравнения можно описать два сложных и взаимосвязанных процесса: возникновение и распространение инноваций. Во-вторых, предложенная модель раскрыла экономистам, занимающимся инновационными процессами, путь в «большую» математику с ее разнообразным инструментарием. Например, авторы показали, что их модель может восприниматься в качестве некоего аналога известного в механике и физике уравнения Дж.М.Бюргерса [4]. В свою очередь уравнение Бюргерса выступает в качестве иллюстрации теории турбулентности, давая тем самым далеко идущие аналогии между экономическими и физическими процессами [5]. Таким образом, обнаруженное внутреннее единство уравнений Бюргерса и Полтеровича–Хенкина открывает возможность проведения междисциплинарных исследований.
Однако модель Полтеровича–Хенкина имеет не только чисто теоретическое значение, но может использоваться и в практических аналитических расчетах. Так, в работе [6] была предпринята попытка применить эту модель к объяснению реальных процессов в черной металлургии. При этом для расчетов использовалась обобщенная модель (3) в следующей форме:
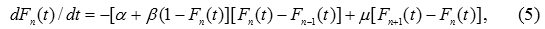
В модели (5) каждое предприятие уровня n поднимается на более высокий уровень n+1 за счет инноваций и заимствования технологий. Одновременно с этим предприятия уровня n+1 опускаются на уровень n с интенсивностью амортизации μ.
Модель (5) исследовалась путем проведения вычислительных экспериментов на основе данных о рентабельности предприятий черной металлургии СССР за 1976-1988 гг. При этом данный период был разбит на два субпериода – 1976-1982 гг. и 1982-1988 гг. Такой шаг был обусловлен тем обстоятельством, что для всего исходного периода не удалось подобрать единые параметры α, β и μ, дающие хорошую аппроксимацию реальных данных, тогда как для субпериодов это оказалось возможным. Данный факт уже сам по себе говорит о наличии принципиального эндогенного сдвига в эффективности отрасли на границе двух субпериодов – в 1982 году.
Говоря о практических аспектах модели (5), следует отметить его индикативное значение. Идентификация параметра α, ответственного за инновационную составляющую, и параметра β, ответственного за имитационную составляющую, позволяет понять сильные и слабые стороны изучаемого объекта (например, отрасли). Сдвиги в величинах α и β для разных периодов сигнализируют о развитии негативных (при их уменьшении) или позитивных (при их росте) тенденциях, что в свою очередь позволяет принимать управленческие решения о корректировке развития объекта.
3. Особенности модели Полтеровича–Хенкина: междисциплинарные аналогии
Не будет ошибкой сказать, что модель Полтеровича–Хенкина имеет большое значение и может считаться определенной вехой в моделировании инноваций. Однако, несмотря на хорошую математическую и теоретическую базу, она имеет свои особенности и ограничения. Рассмотрим некоторые из них подробнее.
Прежде всего, несколько слов о возникновении этого уравнения. Дело в том, что оно напрямую ниоткуда не выводится, являясь в целом весьма специфической и нетривиальной конструкцией. Тогда как к нему следует относиться?
Здесь, на наш взгляд, есть определенная аналогия между уравнением Полтеровича–Хенкина и знаменитым волновым уравнением Э.Шрёдингера, являющимся основой квантовой механики. В свое время в своих лекциях по физике Р.Фейнман писал об уравнении Шрёдингера, что его нельзя вывести и доказать – оно родилось в голове Шрёдингера. В.Босс использовал иную метафору, утверждая, что как музыкант подбирает мелодию, так и Шрёдингер подобрал уравнение колебаний, которое согласовывалось с экспериментальными данными [18]. Иными словами, уравнение Шрёдингера – это некая сложная эвристическая конструкция, у которой нет строгого вывода и доказательства, но которая имеет разные обоснования и предполагает экспериментальную проверку. Более того, справедливость уравнения Шрёдингера подтверждается лишь косвенным образом – совпадением с опытными данными тех следствий, которые из него вытекают [7].
Аналогичным образом уравнение Полтеровича–Хенкина родилось в голове у В.М.Полтеровича, после чего подверглось скрупулезному математическому исследованию. И у этого уравнения также нет строгого вывода и доказательства, а потому оно также предполагает лишь косвенные эмпирические подтверждения.
Еще одна важная особенность уравнения Полтеровича–Хенкина состоит в его дескриптивности, т.е. пассивном описании процесса. Это означает, что данная модель, судя по некоторым обстоятельствам, довольно удачно воспроизводит реальный процесс, но при этом совершенно не объясняет его. На первый взгляд, это кажется странным, однако такое довольно часто встречается как в физике, так и в экономике. Иными словами, в модели увязаны некие ключевые переменные, дающие адекватную искомую траекторию решения, но при этом в ней отсутствуют движущие силы самого моделируемого процесса. Например, уравнение Полтеровича–Хенкина относительно точно воспроизводит эволюцию распределения предприятий по технологиям разного уровня эффективности, но оставляет без ответа вопрос о том, что же именно заставляет предприятия переходить к инновационной или имитационной стратегии. Почему, в частности, одни предприятия переходят к заимствованию более эффективной технологии, а другие – нет? Почему одни это делают быстрее, а другие – медленнее?
Подчеркнем, что, говоря об отсутствии объяснительной схемы в уравнении Полтеровича–Хенкина, мы подразумеваем, что в ней нет соответствующих переменных и механизмов, которые могли бы пояснить возникающие эффекты. Несложно видеть, что в уравнении (3) фигурирует только одна переменная – кумулятивная доля предприятий n-го уровня эффективности; других переменных, качественно отличных от этой, нет. И хотя содержательная трактовка происходящего процесса в принципе понятна, она находится за пределами модели. Механизм эволюции, в явном виде заложенный в модель, слишком прост, а потому и само уравнение относится к классу феноменологических моделей.
К сказанному можно добавить, что существующая аналогия между уравнением Полтеровича–Хенкина и уравнением Бюргерса является чисто формальной, ибо турбулентный процесс, описываемый уравнением Бюргерса, совершенно не похож на процесс «перетекания» предприятий по разным технологиям, описываемый уравнением Полтеровича–Хенкина. Как это ни парадоксально, но гораздо больше аналогий имеется между уравнением Полтеровича–Хенкина и уже упоминавшимся уравнением Шрёдингера. Так, волновое уравнение Шрёдингера описывает локализацию энергии атома по вполне определенным орбитам (дискретным квантовым состояниям), тем самым давая в качестве решения волновой пакет, предполагающий вероятностную трактовку. Соответственно и уравнение Полтеровича–Хенкина описывает рассредоточение производственного потенциала экономической системы по дискретным уровням эффективности, давая в качестве решения волну плотности распределения предприятий. Хотя указанная аналогия является во многом очень условной, она позволяет глубже понять процесс образования направленного распределения (волны) отдельных предприятий (частиц). В дальнейшем образовавшаяся волна эволюционирует как некая непрерывная целостность, состоящая из абсолютно независимых и самостоятельных предприятий. Такое явление напоминает свойство квантово-корпускулярного дуализма света, имеющего в физике фундаментальное значение. При этом уравнение Полтеровича–Хенкина, как и уравнение Шрёдингера, предполагает детерминистскую и вероятностную интерпретацию, а волновая ψ-функция даже по форме очень напоминает волну (4). Опираясь опять-таки на отдаленную аналогию, можно говорить, что технологические уровни в уравнении Полтеровича–Хенкина выступают в качестве своеобразных орбитальных уровней в уравнении Шрёдингера.
4. Содержательная трактовка уравнения Полтеровича–Хенкина
Уравнение Полтеровича–Хенкина имеет одну важную особенность – оно оперирует бесконечным числом технологических уровней, что, конечно же, является нереалистичной гипотезой. Между тем эта гипотеза во многом предопределяет весь моделируемый процесс. В соответствии с уравнением (3) время «работает» против низовых технологий в пользу высших технологических уровней. В соответствии с функцией (4) доля каждого рассматриваемого технологического уровня убывает со временем независимо от того, какой именно уровень нами рассматривается. Но если доля всех уровней убывает, то куда же девается высвободившееся экономическое пространство? Получается либо долевая лакуна, либо мы сталкиваемся с нарушением очевидного условия нормировки, согласно которому сумма всех долей равна единице. Тем самым возникает кажущийся парадокс.
Указанный парадокс преодолевается благодаря использованию в модели бесконечного числа технологических уровней. Фактически уравнение Полтеровича–Хенкина воспроизводит следующий процесс: динамика долей предприятий для каждого известного технологического уровня сопровождается процессом «рождения» новых технологический уровней. На самом деле все эти новые уровни всегда существовали, но их доля была фактически равна нулю, образуя микроскопический довесок к известным уровням и примыкая снизу к величине
С течением времени новые технологии как бы «вываливаются» из этой сингулярности и выдавливают вниз видимые сегодня технологические уровни, т.е. ведут к уменьшению их доли, замещая собой освобождающееся технологическое пространство. В будущем их ожидает аналогичная участь – они будут также «выдавлены» и замещены очередной порцией новых технологий, вываливающейся из технологической сингулярности. При этом время работает в сторону «уплотнения» умирающих технологических уровней путем их сжатия в пренебрежимо малый объем около точки
Таким образом, согласно уравнению Полтеровича–Хенкина в экономике имеется три технологических сегмента: технологическая сингулярность, в которой спрессованы все потенциально возможные новые технологические уровни (их число практически бесконечно); технологическая дыра, в которой также спрессованы все старые, полностью отработанные технологии (их число также не ограничено); промежуточная область реально наблюдаемых технологических уровней, которые находятся в состоянии постепенного «умирания» и вытеснения более прогрессивными технологиями. При этом технологическая сингулярность выступает в качестве генератора инноваций, из которого, как из «черного ящика», вываливаются новые технологии со все более высоким уровнем эффективности. Технологическая дыра, наоборот, как бы поглощает безнадежно устаревшие технологии с низким уровнем эффективности. Указанная направленность процесса приводит к тому, что все вновь родившиеся из состояния сингулярности технологии постепенно устаревают и умирают, «складируясь» в технологической дыре. Схематично данный процесс представлен на рис.1.
Важно рассмотреть и те механизмы, которые приводят весь технологический каскад рис.1 в движение. Таких механизмов два. Первый представляет собой процесс возникновения инноваций и описывается компонентом
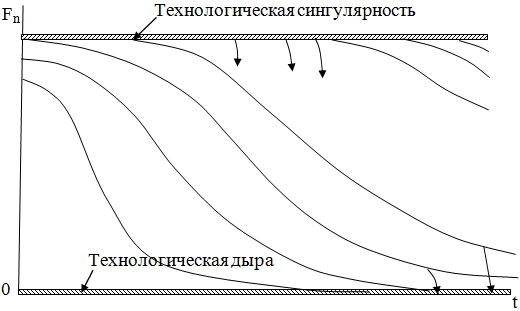
Рис.1. Схема технологической эволюции экономической системы.
Описанный процесс лишний раз показывает его глубокую аналогию с физическими процессами. Так, если по своей математической структуре уравнение Полтеровича–Хенкина напоминает волновое уравнение Шрёдингера, то по характеру моделируемого процесса оно напоминает астрофизический процесс гравитационного коллапса с образованием черной дыры.
Теперь зададимся вопросом о том, что дает нам решение (4). Чтобы получить ответ в более явном виде, следует рассматривать не функцию распределения Fn(t), а функцию плотности

Рис.2. Деформация плотности распределения предприятий во времени.
Учитывая сказанное, можно утверждать, что уравнение Полтеровича–Хенкина дает одну из самых удачных иллюстраций дикретно-волнового единства экономических процессов. В данном случае мы видим, как рациональные действия отдельных предприятий порождают макроэкономическую волну технологического прогресса.
5. Модель Полтеровича–Хенкина и логистическое уравнение диффузии инноваций
Хотя уравнение Полтеровича–Хенкина можно признать верхом математического изящества в воссоздании долговременной эволюции технологической картины экономики, оно все же имеет свои ограничения. Ключевым моментом здесь является гипотеза о бесконечном числе технологических уровней, которая автоматически приводит к положению об их равномерном рождении и умирании. Подобные допущения позволяют эффективно описывать рождение и распространение инноваций в глобальном масштабе, однако для локальных временных периодов такая схема плохо подходит. Для кратко- и среднесрочных процессов характерна крайняя неравномерность инновационных и имитационных сдвигов. Более того, на ограниченном временном отрезке имеет смысл говорить о строго конечном числе технологических уровней.
Иными словами, в ряде случаев желательно от модели с бесконечным числом технологий перейти к модели с конечным числом. Чтобы понять, что в этом случае происходит, рассмотрим простейший случай двух технологий – старой (менее эффективной) и новой (более эффективной). Тогда с учетом того, что

Доля второй технологии определяется тривиально из балансового соотношения:
Несложно видеть, что уравнение (6) представляет собой классическое диффузионное уравнение, дающее в качестве решения логистическую кривую. Однако в правой части уравнения (1) в отличие от логистического уравнения стоит знак минус. Это означает, что рассматриваемая доля y1(t) не возрастает, как это характерно для логистического уравнения, а убывает, как это и требует уравнение Полтеровича–Хенкина. Иными словами, в простейшем случае двух технологий уравнение Полтеровича–Хенкина сводится к обычному логистическому уравнению. Однако в этих двух конструкциях имеет место разная направленность моделируемого процесса. Так, если в диффузионном уравнении моделируется динамика новой технологии, которая вытесняет другую более старую технологию и заполняет рынок, то в уравнении Полтеровича–Хенкина моделируется динамика старой технологии, которая наоборот вытесняется с рынка новой технологией. Можно сказать и так: диффузионное уравнение описывает процесс заполнения и экспансии рынка, а модель Полтеровича–Хенкина – процесс разгрузки и освобождения рынка.
Факт приведения в случае двух технологий уравнения Полтеровича–Хенкина к логистическому уравнению был отмечен еще в работе [8]. Здесь мы лишь заостряем то обстоятельство, что они воспроизводят разнонаправленные процессы. Именно поэтому традиционная логиста является возрастающей функцией, а функция (4) – убывающей. В решениях двух моделей хорошо просматривается указанная инверсия.
Однако переход к двумерной конструкции (6) является не просто конкретизацией уравнения Полтеровича–Хенкина, а его усечением. Что же здесь потеряно?
Дело в том, что в уравнении Полтеровича–Хенкина освобождающееся пространство заполняется множеством других самонарождающихся технологий, тогда как в модели (6) «очищенный» рынок полностью отдается второй технологии, в результате чего формируется почти гомогенный рынок. Иными словами, в уравнении Полтеровича–Хенкина присутствует технологическая сингулярность, порождающая новые технологии, а в диффузионном уравнении такой механизм не предусмотрен. Именно поэтому в логистической модели идет монотонное упрощение структуры рынка, тогда как в уравнении Полтеровича–Хенкина идет постоянная трансформация сложной структуры рынка без снижения степеней свободы.
Тем самым мы подошли к ключевому моменту в сравнении логистического уравнения и уравнения Полтеровича–Хенкина. Второе является «богаче» первого именно за счет появления в нем технологической сингулярности и технологической дыры, которые позволяют поддерживать постоянную технологическую реструктуризацию экономической системы.
6. Эмпирическая проверка уравнения Полтеровича–Хенкина
Как уже было сказано, на практике уравнение Полтеровича–Хенкина может «усекаться», т.е. высшие технологические уровни могут объединяться в одну группу с соответствующей долей предприятий. Такой шаг позволяет в дальнейшем проводить эмпирическую проверку модели.
Подобная работа была проведена в [6] для металлургической отрасли, однако ее результаты требуют специального обсуждения. Здесь следует остановиться, по крайней мере, на четырех обстоятельствах.
Во-первых, правомерность отмеченной процедуры «усечения» остается под вопросом. Дело в том, что при таком подходе фактически нарушается главный постулат модели, а именно: вместо бесконечной технологической шкалы используется малоразмерная конечная шкала. Совершенно очевидно, что никакой альтернативы у этого подхода нет, но, тем не менее, вопрос о нарушении исходной теоретической структуры остается открытым.
Во-вторых, осуществленная аппроксимация реальных данных демонстрирует неустойчивость кривой распределения технологических уровней. Так, расчеты показывают, что не удается построить приемлемое приближение даже для относительно короткого периода – 1976-1887 гг. Данный факт говорит, что «бегущая волна», порождаемая функцией (4), является чрезмерно идеализированным представлением. Согласно (4), форма «бегущей волны» в разные моменты времени почти не меняется. Если «срезать» ее основание, то оставшееся «тело» волны является чрезвычайно устойчивым и бесконечно воспроизводится на разных участках технологической шкалы (рис.2). Однако расчеты показывают, что устойчивость волны сохраняется лишь 6-7 лет (соответственно в 1976-1982 гг. и 1983-1988 гг.). После этого происходит ее сильная деформация, что предполагает построение новой аппроксимации с новыми параметрами. Надо заметить, что подобные расчеты проводились для чрезвычайно консервативной, нединамичной и инновационно пассивной советской экономики. Можно предположить, что в современных экономиках «бегущая волна» будет деформироваться еще чаще, а это уже ставит очень остро вопрос об устойчивости модели (3). Дело в том, что если модель «держится» в течение 1-2 лет, то это почти полностью нивелирует ее прикладное значение, потому что каждый год пересчитывать параметры модели не имеет смысла; в этом случае теряется прогностическая ценность модели.
В-третьих, остается открытым вопрос об эффективности проведенной аппроксимации. Например, для минимизации отклонения между теоретическими и фактическими значениями авторы пользовались методом координатного спуска. Однако такая процедура представляется чисто механической. При подобном подходе получаемые параметры могут не обладать необходимой надежностью. Чтобы определиться с этим вопросом, необходимо построить некий аналог эконометрической модели, которая предполагала бы проверку на адекватность с помощью хотя бы самых простых статистических тестов. Так как подобные тесты не проведены, то осуществленный авторами подгон параметров может восприниматься лишь как точка отсчета для будущих исследований, но не как доказательство прикладной состоятельности модели (3).
В-четвертых, авторами был получен чрезвычайно «скользкий» эмпирический результат: для всех анализируемых периодов модельный параметр α=0. Авторы [6] интерпретируют этот результат как отсутствие инновационной активности в рассматриваемые годы. Однако на самом деле этот результат является чрезвычайно неприятным. Дело в том, что модель (3) является двухфакторной в том смысле, что в ней заложены два механизма трансформации технологического пространства – инновационный и имитационный. Но коль скоро параметр α, отвечающий за инновационный механизм, устойчиво равен нулю, то тогда и вся модель (3) становится уже не двухфакторной, а всего лишь однофакторной, где фигурирует только эффект заимствования технологий. Отсюда можно сделать как «мягкие», так и «жесткие» выводы. Мягкий вывод выглядит примерно так: в рассматриваемые годы в СССР действовала «урезанная» модель Полтеровича–Хенкина с одним механизмом. Жесткий вывод состоит в том, что в уравнении Полтеровича–Хенкина есть избыточный фактор, а, следовательно, и сама спецификация уравнения нуждается в пересмотре. В пользу жесткого вывода говорит тот факт, что в прикладных расчетах авторы [6] использовали зависимость (5), в которой фигурировал третий фактор – параметр выбытия основных фондов (μ). И этот параметр оказался значимым в отличие от параметра α. Следовательно, исходное уравнение нарушается в пользу третьего фактора, изначально в нем не фигурировавшего. Не исключено, что механизм инноваций в пересмотренной модели может и сохраниться, но его формальное описание должно быть иным. На наш взгляд, к истине гораздо ближе мягкий вывод, однако некоторые сомнения все-таки остаются.
Можно отметить некоторую несбалансированность в исследованиях уравнения Полтеровича–Хенкина. Например, разбор математических свойств данной конструкции зашел довольно далеко. В этой связи достаточно упомянуть работу Я.М.Ташлицкой и А.А.Шананина, в которой рассматривается несколько модификаций и усложнений уравнения Полтеровича–Хенкина [10]. Любопытным фактом можно считать, что при отсутствии механизма имитации (β=0) предприятия все равно продолжают переходить на более эффективные технологии, однако при этом функция (4) превращается в более сложную конфигурацию, обладающую некими дополнительными волновыми свойствами.
Между тем практическая апробация уравнения Полтеровича–Хенкина ограничилась всего лишь одной попыткой, где были намечены лишь самые предварительные результаты. На наш взгляд, именно это направление исследований является узким местом в обосновании действенности уравнения Полтеровича–Хенкина. Соответственно именно на этом направлении должны быть сконцентрированы дальнейшие усилия исследователей.
7. Виртуальные технологии в уравнении Полтеровича–Хенкина
Нельзя не отметить тот факт, что само наличие в уравнении Полтеровича–Хенкина технологической сингулярности является чрезвычайно сомнительным методологическим подходом. Фактически речь идет о том, что новые технологические уровни существуют уже в первоначальный момент времени, а потом лишь «активизируются». Иными словами, модель в каждый момент времени оперирует технологиями, которых на самом деле еще нет. Более того, в реальности они могут вообще не возникнуть, тогда как в уравнении Полтеровича–Хенкина этот момент игнорируется. Следовательно, данная модель оперирует виртуальными технологиями, т.е. технологиями которые как бы существуют.
Кроме того, хотелось бы отдельно остановиться на вопросе о рождении инноваций. Дело в том, что практически все существующие сегодня модели с той или иной степенью адекватности описывают, как правило, исключительно процесс распространения инноваций (технологий) по горизонтали, т.е. в направлении завоевания рынка. Однако процесс их возникновения инноваций, предполагающий их движение по вертикали, либо вообще опускается, либо описывается чрезвычайно неудачно. Это связано с тем обстоятельством, что любая инновация имеет субъективное происхождение и рождается в голове у конкретного человека. И этот процесс пока не поддается адекватному описанию. В этом направлении осуществляются только самые первые шаги.
Уравнение Полтеровича–Хенкина не является исключением из этого правила. Например, механизм инновации в нем описывается элементом: -
Как отмечалось, при возникновении инновационных пауз эффект «бегущей волны» подавляется. В этом случае приток новых технологий прекращается, а волна распределения предприятий начинает как бы топтаться на месте с одновременной деформацией своей формы в сторону дрейфа всех предприятий в направлении самой эффективной технологии. В целом же, при переменном параметре α(t) возникает возможность увязать механизмы инноваций и имитации, предложенные Й.Шумпетером, с долгосрочными технологическими циклами. На наш взгляд, данное направление исследования является наиболее интригующим и плодотворным.
8. Теория Полтеровича–Тониса о смене инновационного режима
В модели Полтеровича–Хенкина процессы создания и распространения технологий были объединены в виде непротиворечивого описания. Однако для каждой компании или даже страны очень часто эти два процесса являются взаимоисключающими. Фирме (стране), не являющейся технологическим лидером, приходится постоянно делать выбор между заимствованием готовых новых технологий и самостоятельным созданием таковых. Чем обусловлен этот выбор? Когда происходит переключение с одного режима на другой? Может ли фирма-имитатор превращаться в фирму-инноватора? Каковы закономерности конкуренции двух инновационных механизмов – заимствования и создания новых технологий?
Исследование, в котором была сделана попытка ответить на поставленные вопросы, было осуществлено в статье [13]. В ней построена модель поведения компании, решающей более сложную задачу – выбора между имитацией (заимствованием) уже существующей технологии и созданием новой технологии (собственно инновацией) собственными силами. В более поздней работе [14] было выполнено обобщение предложенной модели. Главная идея указанных работ состояла в учете факта разнонаправленного изменения удельных издержек на имитацию и на инновацию по мере роста технологического уровня компании. Данное положение является центральным для теории Полтеровича–Тониса, которая утверждает наличие некоторой технологической границы (точки), в которой компании (стране) целесообразно переходить от стратегии заимствования к стратегии разработки новых технологий.
Теория Полтеровича–Тониса основана на довольно громоздкой и сложной модели, анализ которой позволяет получить отмеченный теоретический вывод. Однако сердцевиной этой теории является довольно простая гипотеза о принципиально разном влиянии достигнутого технологического уровня на величину удельных издержек по заимствованию и созданию новых технологий. В подтверждение этой теории авторы построили эконометрические зависимости, которые позволили оцифровать их генеральную гипотезу. Так, в работе [13] была получена пара «грубых», простых и симметричных зависимостей применительно к мировой экономике:


В основе инновационной дихотомии теории Полтеровича–Тониса лежат два разнонаправленных эффекта:
Хотя теория Полтеровича–Тониса является весомым вкладом в экономическую теорию, ее сложность и даже некоторая инструментальная избыточность не позволяют ей стать рабочей схемой анализа инновационных процессов. Кроме того, теоретическое доказательство существования технологической границы автоматически ставит задачу по ее количественной идентификации.
Если же говорить о модели Полтеровича–Хенкина, то она задает некие шаблонные траектории технологической диффузии, от которых реальные траектории могут сколь угодно сильно отклоняться. И эти отклонения также нуждаются в систематическом объяснении.
9. Технологическая диффузия и технологические ловушки
Как уже было отмечено, уравнение Полтеровича–Хенкина задает плавные технологические переходы, которые принимают форму технологической диффузии. Однако совершенно очевидно, что это идеализированная схема. Кроме того, не понятна система мотивации предприятий для осуществления инновационных стратегий. Можно ли «расшифровать» микроэкономический механизм принятия решений, лежащий в основе технологической диффузии?
Как оказывается, основой для этого может служить элементарная теория технологических ловушек [15-16]. Речь идет о моделировании переходного процесса, когда некая фирма переходит с одной производственной технологии на другую. Здесь предполагается, что помимо существующей внедренной технологии в экономике уже есть какая-то другая, более прогрессивная технология. Вопрос заключается в том, перейдет или не перейдет на другую технологию рассматриваемая фирма. Иными словами, рассматривается бинарная система принятия инвестиционных решений.
В упрощенной форме переходный процесс сводится к нарушению технологического равновесия [17]:

В соответствии с логикой условия (9) имеет место следующая стратегия компании: если наблюдается точное равенство выгоды и издержек, то имеет место технологическое равновесие, при котором ни одной из технологий нельзя отдать явного предпочтения.
Для упрощения последующего анализа предполагается, что прирост оборота компании постоянен во времени и равен

Бинарная логика смены технологий задается неравенством:

Если неравенство (11) выполняется, то предприятие поднимается на следующий технологический уровень, как это и предполагается во всех диффузионных схемах. В этом пункте хорошо просматривается согласованность диффузионной модели и модели технологических ловушек. Однако условие (11) может и не выполняться; тогда предприятие остается в рамках старого технологического уклада. Если же условие (11) нарушается систематически, то в таких случаях говорят о возникновении технологической ловушки, т.е. о пребывании предприятия в неэффективном технологическом состоянии, несмотря на наличие более прогрессивных технологий [16]. В этом случае технологическая диффузия блокируется, и распространение прогрессивных производственных инноваций прекращается.
Преимущество схемы (11) по сравнению с диффузионными моделями состоит в том, что она объясняет процесс эволюции технологической кривой не с помощью абстрактного эффекта замещения технологий, а с точки зрения рыночной логики принятия решений. Здесь уже имеется более богатая палитра объясняющих переменных: ожидаемый темп роста производства λ, горизонт планирования τ, стоимость новой технологии K(0), выигрыш на текущих издержках от внедрения новой технологии
Случай технологических ловушек особенно интересен, так как он, строго говоря, противоречит схеме, лежащей в основе уравнения Полтеровича–Хенкина. Содержательно это означает, что процесс технологической диффузии прекращается, а технологический уровень предприятий, попавших в технологическую ловушку, с течением времени не «вдавливается» в технологическую дыру, а как бы замораживается на определенной доле. Если при этом из технологической сингулярности будут по-прежнему «сыпаться» новые технологии, то это приведет к тому, что каждая последующая волна yn(t) на рис.2 будет растягиваться вдоль оси и одновременно расплющиваться. Параллельно, скорее всего, будет меняться ее форма, а именно: она будет все более покатой слева и все более отвесной справа. Таким образом, феномен технологических ловушек способен привести с серьезной деформации волны yn(t), делая ее все более асимметричной.
Заметим, что противоречие между моделью Полтеровича–Хенкина и теорией технологических ловушек возникает только в случае возникновения сопротивления естественному ходу технологической диффузии со стороны предприятий, попавших в технологическую ловушку; в противном случае схема ловушек более полно раскрывает механизм того, что описывает схема Полтеровича–Хенкина.
Если теорию технологических ловушек распространить на случай множества технологий, то полученные таким образом формулы позволяют установить несколько фактов [17]. Во-первых, при недостаточном потенциале роста компаний технологическая диффузия может вообще прекращаться, перерождаясь в технологическую ловушку и технологический застой. Во-вторых, иногда может возникнуть условие тотальной технологической ловушки, когда любые инновации становятся невозможны. Такое возникает, когда удорожание новых технологий происходит слишком быстро по сравнению с увеличением их эффективности, а потенциал роста компании недостаточен, чтобы «пересилить» сложившиеся негативные условия. В-третьих, почти всегда имеет место неравномерность технологической диффузии, когда происходит заимствование технологии не следующего уровня, а более высокого ранга; за счет этого возникает нарушение ступенчатого и последовательного технологического прогресса. В-четвертых, технологическая диффузия замедляется по мере приближения компании к технологическому лидеру.
Перечисленные свойства технологической диффузии дают непротиворечивое и прозрачное представление о характере процесса заимствования технологических инноваций. Главное же достоинство модели ловушек состоит в том, что она хорошо объясняет фактические отклонения реальных стратегий предприятий от идеальной траектории, предписываемой диффузионными моделями.
10. Определение технологической границы
Дальнейшее развитие модели технологических ловушек позволило рассмотреть процесс перехода компании с i-го технологического уровня на l-ый уровень. В этом случае усложненное условие технологического равновесия имеет вид:
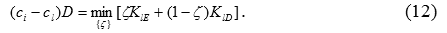
Модель (12) фактически задает правило инвестирования при наличии выбора между вложениями в заимствование и в создание технологий.
Если исходить из действия двух эффектов


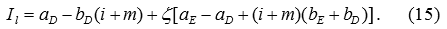
Из (15) вытекает, что

Это означает, что имеет место свойство:
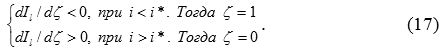
Из (17) вытекает следующее правило инвестирования: если исходный технологический уровень компании не достаточно высок, то она использует стратегию заимствования технологий; в противном случае она использует инновационную стратегию. В первом случае компания предпочитает закупать ноу-хау и сами технологии, во втором – старается сама осуществлять исследования и разработки с последующим производством новой технологии. Таким образом, простая модель бинарного выбора подтверждает эффект, содержащийся в теории Полтеровича–Тониса и состоящий в существовании технологической границы, превышение которой стимулирует переход от имитационных стратегий к инновационным.
Однако, помимо чисто теоретических выводов, модель (12) дает простой способ оценки самой технологической границы. Дело в том, что эконометрические зависимости (7) и (8) являются конкретизацией формул (13) и (14). Это означает, что для расчетов можно воспользоваться формулой (16), которая дает величину технологической границы i*=61,5%. Это означает, что компания (или страна), достигшая значения эффективности (например, производительности труда) в 61,5% от лидера, имеет достаточно оснований для отказа от стратегии заимствования и переходу к разработке новых технологий.
Разумеется, полученная цифра может служить лишь в качестве первого приближения, однако факт получения указанной технологической константы уже сам по себе имеет большое теоретическое и практическое значение.
Рассмотренные в данной статье модели и закономерности рождения и распространения инноваций отнюдь не исчерпывают данной тематики. Они, скорее, создают неплохую теоретическую основу для дальнейших поисков экономических эффектов в инновационной и инвестиционной сфере. Например, сегодня уже имеются попытки перенесения диффузионных закономерностей на динамику институтов [17; 19]. Так, Е.В.Попов предлагает описывать динамику трансакционных издержек компании диффузионным уравнением А.Фика (вторым законом Фика) [19]. Однако в этой конструкции, как и во всех диффузионных схемах, отсутствует факт рождения новых институтов и их взаимной конкуренции. В этом смысле уравнение Фика может быть модифицировано для более полного учета обоих инновационных механизмов. Аналогичным образом подобные аналитические зависимости могут быть применены к описанию процессов рождения и распространения знаний, в отношении которых накоплена определенная эмпирическая база [20]. Кроме того, подобные процессы могут быть эффективно «расшифрованы» и объяснены посредством использования теории технологических и институциональных ловушек.
Литература
- Гельман Л.М., Левин М.И. Модели инновационных процессов (обзор зарубежной литературы)// «Экономика и математические методы», №6, 1989.
- Полтерович В.М., Хенкин Г.М. Эволюционная модель взаимодействия процессов создания и заимствования технологий// «Экономика и математические методы», №6, 1988.
- Полтерович В.М., Хенкин Г.М. Эволюционная модель экономического роста// «Экономика и математические методы», №3, 1989.
- Henkin G.M., Polterovich V.M. A difference-differential analogue of Burgers equation and some models of economic development/ Working Paper #WP/98/051, Moscow, CEMI of Russian Academy of Science, 1998.
- Burgers J.M. A mathematical model illustrating the theory of turbulence/ Advances in Applied Mechanics. Ed. R.V.Mises and T.V.Karman. 1948.
- Гельман Л.М., Левин М.И., Полтерович В.М., Спивак В.А. Моделирование динамики распределения предприятий отрасли по уровням эффективности (на примере черной металлургии)// «Экономика и математические методы», №3, Том 29, 1993.
- Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов. 8-е изд. М.: Издательство Оникс; Мир и образование, 2006.
- Балацкий Е.В. Моделирование процессов межсекторальной конкуренции// «Общество и экономика», №5, 2008.
- Полтерович В.М. Гипотеза об инновационной паузе и стратегия модернизации// «Вопросы экономики», №6, 2009.
- Ташлицкая Я.М., Шананин А.А. Моделирование процесса распространения технологий. М.: Вычислительный центр РАН, 2000.
- Норт Д. Понимание процесса экономических изменений. М.: Изд. дом ГУ-ВШЭ, 2010.
- Попов В.В. Почему Запад разбогател раньше, чем другие страны, и почему Китай сегодня догоняет Запад? Новый ответ на старый вопрос// «Журнал Новой экономической ассоциации», №3(15), 2012.
- Polterovich V., Tonis A. Innovation and Imitation at Various Stages of Development// Moscow, New Economic School, 2003.
- Polterovich V., Tonis A. Innovation and Imitation at Various Stages of Development: A Model with Capital// Working Paper #2005/048, Moscow, New Economic School, 2005.
- Балацкий Е.В. Функциональные свойства институциональных ловушек// «Экономика и математические методы», №3, 2002.
- Балацкий Е.В. Экономический рост и технологические ловушки// «Общество и экономика», №11, 2003.
- Балацкий Е.В. Технологическая диффузия и инвестиционные решения// «Журнал Новой экономической ассоциации», №3(15), 2012.
- Босс В. Интуиция и математика. М.: Издательство ЛКИ, 2008.
- Попов Е.В. Трансакции. Екатеринбург: УрО РАН, 2011.
- Попов Е.В., Власов М.В. Институты знаний. Екатерингбург: Институт экономики УрО РАН, 2012.



































Написать комментарий