Управление государственным долгом является большим искусством. На что можно опереться при решении этой задачи? Есть ли модели, позволяющие упростить эту задачу? Какие задачи надо одновременно решать при разработке долговой политики? Как это все можно рассчитать?
Невозможность экономического роста при слишком высоких темпах инфляции доказана как теоретически, так и эмпирически (см., в частности, [1,2]). Финансовая стабилизация и достижение инфляционного равновесия требуют жесткого ограничения денежно-кредитной эмиссии. Важным способом сдерживания цен является “перекладывание” эмиссионных проблем на регуляторы открытого рынка, достигаемое путем частичного переключения проблем чисто монетарного управления на инструменты учетно-долговой политики государства. Однако подобный способ достижения макроэкономической стабилизации также таит в себе множество проблем, которые при неблагоприятных обстоятельствах могут вырваться из-под контроля. В данной статье мы рассмотрим существующие общие закономерности в динамике интернальной (внутренней) и экстернальной (внешней) государственной задолженности и сформулируем ряд управленческих принципов, с помощью которых может быть повышена результативность всей долговой политики государства. Важное значение при рассмотрении проблемы динамики государственного долга имеет тесное переплетение долговой, монетарной и бюджетной стратегий государства, включая меры по антициклическому регулированию и стимулированию инвестиционной и производственной активности.
1. МОДЕЛЬ ДИНАМИКИ ИНТЕРНАЛЬНОГО ГОСУДАРСТВЕННОГО ДОЛГА
Формализуем процесс образования интернального долга и изучим соответствующие динамические траектории. Весьма простая и элегантная модель движения доли внутреннего долга в национальном продукте была предложена Л.Е.Соколовским в 1991 г. [3]. Однако он, во-первых, не провел тщательного анализа возможных режимов “расползания” государственного долга, а, во-вторых, не довел сконструированную им модель до численного наполнения и, соответственно, количественно не идентифицировал текущую ситуацию и не определил перспективы экономического развития в данной сфере. Попытаемся восполнить пробелы в монетарно-долговой проблематике по названным двум направлениям с учетом некоторых инструментальных дополнений. Используя те же исходные посылки и базовые соотношения, которые были рассмотрены Л.Е.Соколовским, будем опираться на представление о дискретности процесса и построим итоговую модель в виде не дифференциального, а разностного уравнения. Разумеется, будет несколько скорректирована и сама методология моделирования, учитывающая разновременные эффекты.
Пусть D - дефицит государственного бюджета; G - государственные расходы (исключая расходы по обслуживанию государственного долга); T - государственные доходы (налоговые поступления); B - долг по государственным ценным бумагам; r - номинальная процентная ставка по долговым обязательствам государства; t - период времени (в данном случае - год). Тогда

Если ввести понятие средней ставки налогообложения

Так как бюджетный дефицит финансируется за счет долга и денежно-кредитной эмиссии, то имеем

Введя приростной коэффициент монетизации долга

Завершает формальное описание очевидное рекуррентное соотношение для интернального долга

Соотношения (1), (3) и (5) образуют искомую модель процесса. Используя показатели индекса цен (инфляции)
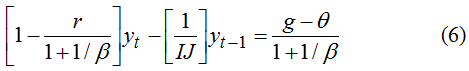
Несмотря на то, что уравнение (6) достаточно точно воспроизводит исследуемый процесс, в практических расчетах оно не совсем удобно из-за наличия коэффициента β, который в явной форме отражает государственные приоритеты в проведении монетарно-долговой политики. Чтобы избавиться от такого нежелательного показателя, следует переписать соотношение (3) в виде

Тогда с учетом того, что
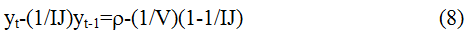
Учитывая
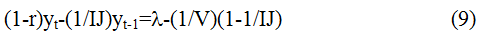
Если рассматривать только стационарные траектории экономического развития, когда показатели I, J, V и λ стабильны во времени, то модель (9) представляет собой простейшее неоднородное разностное уравнение с постоянными коэффициентами, решением которого является функция (C0 - константа, зависящая от начальных условий) [4-5]
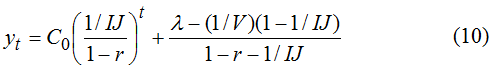
В большинстве случаев целесообразно использовать понятие не номинальной r, а реальной (продефлированной) процентной ставки r* по государственным ценным бумагам: r*=r-(I-1). В этом случае (10) перепишется в виде
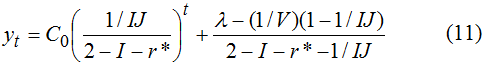
Полученное уравнение (11) описывает динамические траектории доли интернального долга в валовом внутреннем продукте и позволяет проанализировать стратегию государства в отношении управления ее величиной в зависимости от складывающейся монетарной обстановки (V, I), уровня экономической активности (J) и проводимой долговой (r*) и фискально-бюджетной (g, θ) политики.
Несмотря на явную простоту, формула (11) позволяет, во-первых, качественно проанализировать ряд важных аспектов долговой политики, а, во-вторых, количественно оценить некоторые эффективные границы экономических параметров, в рамках которых возможно достижение финансовой стабилизации.
2. АНАЛИЗ ДИНАМИКИ ВНУТРЕННЕГО ДОЛГА
Как видно из (11), относительная величина внутреннего долга складывается из динамической и статической составляющих (соответственно, первый и второй компоненты правой части (11)). При этом весьма любопытным представляется существующее между ними определенное противоречие. Проанализируем возникающие эффекты более подробно, выделив пять ключевых моментов.
Во-первых, формула (10) позволяет теоретически определить эффективную инфляционную границу, которую эмпирически идентифицировать просто невозможно. Дихотомия инфляционных режимов задается соотношением


Если правая часть (12) больше левой, то относительная величина внутреннего долга возрастает; в противном случае объем долга тяготеет к динамическому затуханию. Здесь мы сталкиваемся с чрезвычайно важным и тонким аспектом экономической динамики. Дело в том, что сегодня уже очевидна необходимость ненулевой положительной инфляции - об этом свидетельствуют как практический опыт, так и теоретические работы по ценообразованию и экономическому равновесию (см., например, [6]). С другой стороны, существуют различные подходы к оценке предельно допустимых темпов инфляции, за пределами которых экономический рост становится невозможен [1-2]. Однако до сих пор остается открытым вопрос о количественной оценке минимального темпа инфляции, выгодного государству. Ответ напрямую связан с монетарной политикой в смысле обеспечения оптимальных темпов прироста денежной массы. Формула (12) позволяет ответить на этот вопрос, а именно: темпы инфляции, содействующие погашению государственного долга, должны быть такими, чтобы левая часть (12) была меньше правой. Минимальный индекс роста цен определяется непосредственно из равенства (12). Таким образом, в долгосрочном аспекте государство должно поддерживать определенный инфляционный паритет. С теоретической точки зрения это достаточно очевидно, так как инфляция “съедает” долги государства.
Во-вторых, даже при благоприятном экономическом режиме, когда yt тяготеет к затуханию, доля внутреннего долга всегда имеет свой естественный предел - минимальное значение ymin, определяемое правой частью (11):
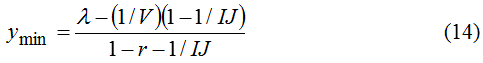
В данном случае статический компонент в (10) выступает в качестве асимптоты, ниже которой величина yt упасть не может (см. рис.1). Если λ>(1/V)(1-1/IJ)>0, то нижняя граница ymin находится в положительном ортанте (знаменатель в (13) полагаем положительным). Чтобы устранить лимитирующий эффект ymin, уровень относительного текущего бюджетного дефицита необходимо сократить до величины
| Сценарий расчета | Среднегодовой индекс роста цен (I) | Среднегодовой индекс роста производства (J) | Номинальная годовая ставка процента по государственным ценным бумагам (r), % | Характер динамики доли внутреннего долга в ВВП |
|---|---|---|---|---|
| №1 | 1,05 | 1,04 | 9,0 | Возрастание |
| №2 | 1,05 | 1,04 | 7,0 | Убывание |

Соответственно, на практике бюджетная политика должна быть построена таким образом, чтобы фактические значения λ лежали в интервалах 0<λ< λmax. Любопытно, что в условиях, при которых интернальный долг уменьшается, между показателями y и λ прослеживается положительная связь:
| Сценарий расчета | Скорость обращения денег (V), об/год | Относительный уровень бюджетного дефицита (λ), % | Значения доли внутреннего долга в ВВП, % | Время перехода из начального состояния в конечное (T), лет | |
|---|---|---|---|---|---|
| начальное (yн) | конечное (yк) | ||||
| №1.1 | 7,5 | 5,0 | 2,0 | 10,0 | 1,7 |
| №1.2 | 7,5 | 5,0 | 2,0 | 20,0 | 4,0 |
| Сценарий расчета | Относительный уровень бюджетного дефицита (λ), % | Допустимые границы доли внутреннего долга в ВВП, % | Минимально возможный уровень доли внутреннего долга в ВВП (ymin), % | |
|---|---|---|---|---|
| нижняя (λmin) | верхняя (λmax) | |||
| №2.1 | 1,2 | 0,9 | 1,1 | 7,0 |
| №2.2 | 2,0 | 0,9 | 1,1 | 56,0 |
В-третьих, из (10) вытекает специфическая зависимость долга от темпа инфляции. Так, например, если λ> λmax, а знаменатель в (13) положителен, но близок к нулю, то ymin→∞; если знаменатель в (13) отрицателен, то ymin→-∞. Подобные эффекты весьма опасны и, по сути, дела лишают бюджетную политику каких-либо альтернатив: уровень бюджетного дефицита должен поддерживаться в границах 0lt;λ< λmax. В противном случае приближение ситуации к режиму, определяемому дихотомической гранью (12), может привести к возникновению своего рода долговой ловушки. В сжатые сроки выбраться из такой долговой ямы государству вряд ли удастся, что и обусловливает необходимость жесткой бюджетной политики.
В-четвертых, увеличение темпов инфляции и экономического роста ведет к сокращению минимальной величины доли внутреннего долга в валовом продукте
Таким образом, мы получили еще одно важное дихотомическое условие:


Отсюда видно, что множество {λ} является непустым только при

Условие (18) устанавливает достаточно узкий диапазон эффективных номинальных процентных ставок по государственным ценным бумагам и тем самым существенно ограничивает долговую политику правительства.
Неравенства (17) связаны с еще одним важным моментом, имеющим общефилософское значение. Дело в том, что в современном мире достаточно четко прослеживается долгосрочная тенденция к снижению скорости обращения денег: V→0 при t→∞ (для США соответствующий вековой тренд приводится в [7]). Однако в этом случае и правая и левая границы в (17) тяготеют к бесконечности. Учитывая, что эффективные значения {λ} зажаты между двумя бесконечно большими значениями, сами λ также оказываются неограниченно высокими: λ→∞ при t→∞. Таким образом, любые попытки ликвидации внутреннего государственного долга выдвигают требование дефицитного финансирования, причем при неблагоприятной тенденции к замедлению оборачиваемости платежных средств уровень бюджетного дефицита будет принимать бесконечно высокие значения. Подобное развитие событий в длительной перспективе эквивалентно разрушению самого института государства.
В данном случае мы теоретически доказали известный тезис Д.Бьюкенена о том, что в условиях демократических институтов власти государственный долг, выражающий расточительность государства, раз возникнув, не только не имеет тенденции к уменьшению, но, скорее всего, будет постоянно возрастать [3].
Сказанное подтверждается хроническим дефицитом бюджетов большинства государств мирового сообщества. Наиболее ярко тенденция к росту долга и бюджетного дефицита прослеживается в США, что позволяет авторам [8] уже сейчас говорить об общественном апокалипсисе современных экономических систем из-за вырвавшегося “зверя” из бюджета. Указанный эффект вскрывает одно из фундаментальных противоречий механизма социально-экономического развития.
В-пятых, из (10) вытекает условие возникновения периодически нарастающих колебаний доли внутреннего долга в валовом продукте: r>1. При r<1 величина yt плавно увеличивается или убывает. Хотя условие (18) автоматически предполагает отсутствие неустойчивых траекторий и оно более сильное, чем условие r<1, само по себе понимание характера динамики внутренней задолженности при номинальной процентной ставке по государственным ценным бумагам больше 100% годовых является весьма ценным. Действительно, возникающая при этом пилообразная траектория с нарастающей амплитудой колебаний с точки зрения задачи по обеспечению равномерности экономического развития просто недопустима.
Следует заметить, что полученные ограничения на величину процентной ставки по долговым обязательствам государства автоматически ставят достаточно жеский инфляционный барьер:

Условие (19) сводится к квадратному неравенству:

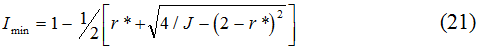
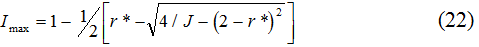
Выявленная инфляционная дихотомия представлена на рис.5, где штриховкой обозначен коридор допустимых значений индексов инфляции.
В данном случае прослеживается органичная связь между монетарной и долговой политикой государства; совместное использование монетарных и долговых рычагов предполагает взаимное ограничение их эффективности.
В заключение укажем еще одну “опасную” точку в макроэкономической стратегии управления интернальным долгом: r=1. Такое состояние теоретически означает катастрофу для динамики величины yt. Из сказанного следует, что государство должно избегать подобного режима, так как вхождение в него означает начало развития долгового кризиса.
3. ДОЛГОВАЯ ПОЛИТИКА И ИНВЕСТИЦИОННАЯ АКТИВНОСТЬ
Выше мы рассмотрели закономерности в динамике внутреннего государственного долга в зависимости от темпов инфляции и экономического роста. Однако не менее важным представляется и влияние долговой политики государства на деловую активность в стране. Данной проблеме посвящено множество работ западных экономистов [9]. Однако большинство предлагаемых модельных построений, во-первых, является весьма сложным в формальном отношении, а, во-вторых, переносит центр тяжести экономического анализа на выяснение роли налоговых инструментов в регулировании поведения экономических агентов и специфики межвременного взаимодействия поколений. При этом сами налоги рассматриваются в качестве финансового субститута интернального долга. На наш взгляд, заменить долговые обязательства государства может только денежно-кредитная эмиссия, что и было отражено при построении модели (9). В этом случае анализ фискальных эффектов скорее лишь еще больше запутывает, чем проясняет общую ситуацию. Вместе с тем остается открытым вопрос о целесообразности государственных займов с точки зрения их воздействия на инвестиционную восприимчивость экономики и объемы производства. Попытаемся исследовать эту проблему с помощью простейших дескриптивных аналитических схем.
Мы считаем, что величина внутреннего долга представляет собой прямой вычет из суммарных народнохозяйственных инвестиций. Дело в том, что осуществляемые займы используются государством для покрытия бюджетного дефицита, то есть в основном на поддержание общественного сектора экономики. Предположение о возможности вложения долговой суммы в создание капитальных благ [3; 9] фактически ничего не меняет в наших рассуждениях, так как любые государственные расходы являются вынужденными и направлены на поддержание и укрепление института государства.
В контексте сказанного величина частных инвестиций K задается следующим соотношением:

В соответствии с кейнсианской доктриной, по мере роста процентной ставки r привлекательность государственных ценных бумаг возрастает, а, следовательно, увеличивается величина ΔB и суммарный объем инвестиций сокращается. Частично данный эффект компенсируется реинвестированием дохода, получаемого по уже приобретенным государственным обязательствам (первое слагаемое в правой части (23)). Конкретная величина инвестиций и интернального долга в (23) складывается в результате эндогенной балансировки процентной ставки r и фактической нормы прибыли в реальном секторе экономики. Если
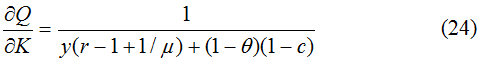
Из уравнения (23) видно, что долговая политика государства не ухудшает инвестиционную ситуацию только в случае, если сумма первого и второго компонентов в (23) положительна, то есть при

При разработке макроэкономических ориентиров целесообразно ограничивать накачивание государственных долгов в соответствии с неравенством (25). Однако в этом случае мультипликатор (24) оказывается меньше стандартного мультипликатора инвестиций, в котором полагается y=0 [10]. Важно также и то, что при y→∞ и r→∞ мультипликатор (24) постепенно обнуляется: ∂Q/∂K→0. Это означает, что, не влияя на естественный объем инвестиций, долговая политика подрывает их эффективность. В этом заключается еще одно противоречие долговой стратегии государства с точки зрения экономической динамики.
Если предположить, что объем инвестиций и цены стабильны, то (23) можно рассматривать как неявную функцию Q(y), которая может быть найдена из дифференциального уравнения [11]
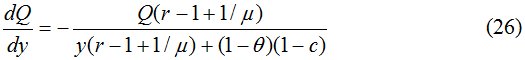
С учетом того, что Q=PX из (26) имеем
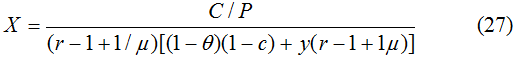
Зависимость (27) показывает, что в стабильной ценовой и инвестиционной среде любой рост доли внутреннего долга в валовом продукте, независимо от параметрических конфигураций, приводит к снижению производства, что, вообще говоря, и доказывает необходимость борьбы с государственной задолженностью. Хотя подобная статичность ситуации является явной идеализацией, все же из нее виден принципиальный характер той роли, которую играет государственный долг в жизни общества.
Интересный результат может быть получен из дополнительного анализа (24) и (27). Во-первых, при значениях

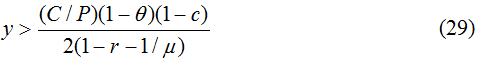
Из (29) следует, что если долговая политика проводится достаточно аккуратно и условие (25) выполняется, то ограничение (29) выполняется при любых значениях интернального долга и рост процентных ставок позитивно сказывается на производственной активности. В противном случае правая часть (29) становится положительной и недостаточно большой удельный вес долга в валовом продукте означает подрыв производственного климата любым увеличением процентных ставок. Условие (29) определяет также предельно допустимые процентные ставки, исходя из уже достигнутого уровня государственной задолженности. Сказанное подводит к пониманию серьезности условия (25) и требует обязательного его выполнения при разработке конкретных вариантов долговых стратегий государства. Несмотря на свою простоту принцип (25) должен быть одним из главных при управлении внутренним долгом.
4. КОЛИЧЕСТВЕННАЯ ОЦЕНКА ЭФФЕКТИВНЫХ ГРАНИЦ ДОЛГОВЫХ СТРАТЕГИЙ ГОСУДАРСТВА
Рассмотренные нами стационарные траектории развития достаточно абстрактны. Особенно это характерно для переходного периода, когда динамика подавляющего числа экономических переменных имеет сложный колебательный характер. Тем не менее полученные количественные ограничения позволяют хотя бы приблизительно установить эффективные границы варьирования управляемых экономических параметров и делать ориентировочные прогнозные расчеты. Перейдем к более предметному рассмотрению численных закономерностей.
Для оценки условий, при которых имеет место долговременная тенденция к уменьшению доли внутреннего долга в валовом продукте разработаем два гипотетических сценария с достаточно “хорошими” экономическими характеристиками (таблица 1). Ключевым условием, подлежащим проверке, является неравенство (17).
Расчеты показывают, что для сценария №1 условие (17) не выполняется и в долгосрочной перспективе доля yt имеет тенденцию к возрастанию. Для сценария №2, напротив, условие (17) выполняется как строгое неравенство и величина yt тяготеет к затуханию. При этом, как видно из таблицы 1, сценарии различаются только величинами процента, расхождение между которыми составляет всего лишь 2% годовых. Однако этого достаточно, чтобы принципиально изменить экономический режим в отношении динамики внутреннего долга. Таким образом, первый вывод, который можно сделать по результатам расчетов, состоит в том, что при достаточно благоприятных экономических параметрах динамика доли внутреннего долга в валовом продукте чрезвычайно чувствительна к любым изменениям номинальной ставки процента по государственным ценным бумагам; смещение ставки r всего лишь на 1-2% может радикально изменить тип развития экономической системы.
Из таблицы 1 видно, что для сценария №1 реальная ставка процента r* составляет 4%, а для сценария №2 - 2%. Это означает, что если государство стремится к долговременному снижению величины yt , то оно должно строить свою долговую политику таким образом, чтобы доход по государственным ценным бумагам незначительно покрывал темпы инфляции; реальный доход от них не должен превышать 1-2% в год. Такой низкий процент можно считать вполне обоснованным, если учесть, что доход по государственным ценным бумагам является гарантированным и относится к разряду безрисковых. Однако, учитывая возможность получения инвесторами более высоких доходов от вложений в частный сектор экономики при довольно незначительном риске, можно утверждать, что реальный годовой доход в 1-2% вряд ли может создать значительный спрос на государственные долговые активы. Таким образом, аккуратная долговая политика, обеспечивающая выполнение (17), на практике слабо реализуема, что составляет второй вывод из полученных количественных оценок.
Таким образом, что в нормальных экономических условиях государственный долг, раз возникнув, может, как правило, только возрастать, что лишний раз подтверждает ранее упоминавшийся тезис Д.Бьюкенена. Следовательно, вопрос состоит лишь в скорости подобного возрастания. Соответственно, государство может настраивать управляемые макропараметры так, чтобы обеспечить максимально медленный рост внутренней задолженности. Что касается режима, когда (17) истинно, то его вырождение и нереализуемость вытекает также из того факта, что, согласно расчетам, в большинстве случаев ymin>1, что не имеет экономического смысла и равносильно полному банкротству государства. Это означает, что тенденция к росту удельного веса государственной задолженности в валовом продукте страны по существу является безальтернативной. Каковы же темпы увеличения бюджетной задолженности?
Для ответа разобьем исходный сценарий №1 на два субсценария и дополним их соответствующими экономическими параметрами (таблица 2). При этом значения характеристик V и λ близки к отчетным данным о состоянии российской экономики в 1995г. Наша посылка о двухпроцентном начальном уровне внутреннего долга yн представляется весьма реалистичной для стационарно развивающейся экономики. Конечные значения yк доли государственной задолженности в 10% и 20% отражают весьма опасные состояния в развитии процесса, что делает особенно интересной оценку периода T, в течение которого yt пробегает расстояние [yн; yк].
Расчет T проводился по следующей формуле, вытекающей из (10):
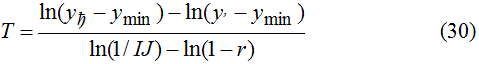
Результаты расчетов приведены в таблице 2 и позволяют сделать третий важный вывод: даже при достаточно благоприятных условиях (низких темпах инфляции и высоких темпах экономического роста) скорость нарастания внутреннего государственного долга чрезвычайно высока. Фактически за 5 лет изначально почти незаметное долговое бремя способно достичь уровня национального бедствия. Разумеется, из-за нестационарности развития реальной экономики окончательные критические показатели являются меньшими. Однако в целом модель (9) дает правильную картину присходящих событий.
Теперь более предметно коснемся вопроса о взаимных ограничениях долговой и бюджетной политики государства, а именно: какой уровень текущего бюджетного дефицита должен поддерживаться, чтобы обеспечить полное погашение внутреннего государственного долга? Для этого оценим границы λmin и λmax для рассмотренного нами сценария №2, который также разобьем на два субсценария с различными фактическими значениями λ (таблица 3).
Согласно расчетам полная ликвидация внутренней задолженности в нашем примере возможна только при сверхжесткой бюджетной политике государства в расходовании своих средств. Полученное эффективное значение относительного бюджетного дефицита, которое составляет всего лишь 1% от валового внутреннего продукта, чрезвычайно сложно поддерживать в длительной перспективе. Однако опыт показывает, что некоторым странам удается добиться даже положительного бюджетного баланса [2]. Проведенные расчеты показывают также, что в случае даже незначительного превышения эффективной границы λmax нарушается неравенство

Отсюда следует четвертый вывод: при однажды выбранной стратегии в отношении постепенной ликвидации внутреннего долга правительство должно неуклонно следовать жесткому курсу по удержанию бюджетного равновесия; любые послабления в сторону дефицитного финансирования окажут разрушительное воздействие на величину государственной задолженности.
Заметим, что в расчетах мы использовали предпосылку λ=const. Однако в реальности λ также возрастает. Это происходит, в частности, вследствие действия закона А.Вагнера, согласно которому ∂g/∂X>0 или, что то же самое, H/J>1, где
5. ВЗАИМНАЯ КОНВЕРСИЯ ИНТЕРНАЛЬНЫХ И ЭКСТЕРНАЛЬНЫХ ДОЛГОВ
Выше была показана определяющая роль уровня текущего бюджетного дефицита для динамики внутреннего долга. Кроме того, доказано, что в ряде случаев, когда нарушается условие (17), погашение долговых обязательств государства вообще становится невозможным даже в отдаленной перспективе. Отсюда логичным образом возникает вопрос: что делать, если текущий дефицит все-таки превысил отметку λmax? По-видимому, свое слово в решении данной проблемы может сказать экстернальная задолженность страны. Однако в этом случае возникает чрезвычайно сложная проблема координации динамики внутреннего и внешнего долгов. По сути дела перед государством встает задача максимально пролонгировать выплату всех своих долгов за счет будущих налоговых поступлений. Возможности же мгновенного увеличения текущих налоговых ставок во многом иллюзорны. Это связано с тем, что налоговый пресс в нормальных условиях всегда завинчен почти до предела и малейшее его увеличение может привести к перемещению экономики на нисходящую ветвь кривой А.Лаффера и возникновению депрессивного эффекта в сфере производства. Помимо этого, мы не учитывали структуру интернального долга, также имеющую большое значение. Действительно, манипулирование объемами краткосрочных и долгосрочных государственных ценных бумаг является одним из мощных инструментов эффективной долговой политики [13].
Указанные моменты являются достаточно тонкими и в модели (9) никак не отражены. Вместе с тем внутренняя и внешняя долговые стратегии осуществляются параллельно и на деле неразрывно взаимосвязаны. Особенно важны эффекты, связанные с конверсией внешнего долга во внутренний и наоборот, также как и взаимная трансформация краткосрочных и долгосрочных займов. Подобные структурные сдвиги в государственных финансах ведут к изменению начальных условий и, соответственно, всей последующей динамики анализируемых переменных. Таким образом, модель (9), вообще говоря, нуждается в модификации и обобщении. Рассмотрим общие контуры такого случая.
Пусть B′ и B′′ - величины долговых обязательств государства соответственно по долгосрочным и краткосрочным ценным бумагам; r′ и r′′ - процентные ставки по долгосрочным и краткосрочным ценным бумагам; B0 и r0 - объем внешнего долга и процент по нему; ε - валютный курс. В этом случае модель (1), (3), (5) преобразуется к виду:
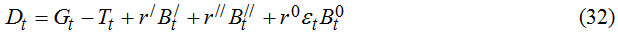
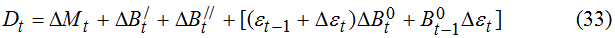



В соотношениях (32) и (33) величина Dt как и ранее играет роль “полного” бюджетного дефицита, выраженного в национальной валюте; выражение в квадратных скобках в (33) показывает величину прироста внешнего долга в национальных денежных единицах. В общем случае модель (32)-(36) сводится к системе из трех разностных уравнений, анализ которых в явной форме затруднен. Однако, если регулирующие органы поддерживают постоянной структуру государственной задолженности, то построенная модель значительно упрощается. Опуская промежуточные выкладки, запишем уравнения динамики относительных долей государственного долга y′, y′′ и y0, где
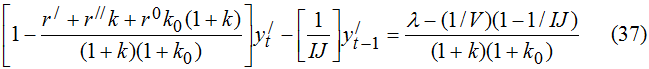

Более сложным является уравнение динамики внешнего долга:
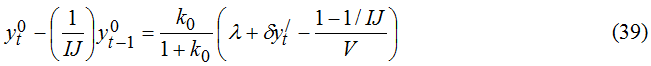
Таким образом, в нашем случае динамика внутреннего долга в значительной мере определяет динамику внешнего в условиях выбранной структуры долговых активов государства. При этом стационарная траектория относительной величины долгосрочной задолженности государства описывается уравнением
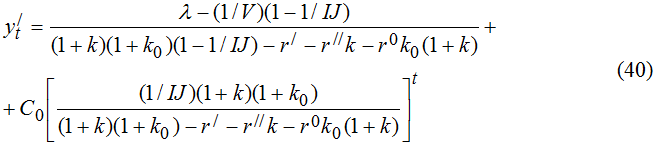
Динамика краткосрочных долговых активов подчиняется соотношению (38), а движение доли внешнего долга в национальных денежных единицах происходит в соответствии со следующим уравнением (см. Приложение)
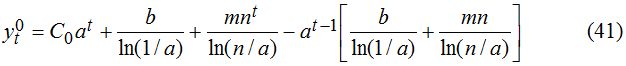

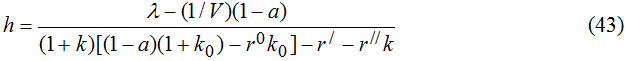

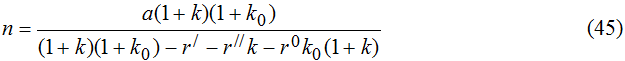
Получившиеся соотношения (38), (40) и (41) позволяют детально анализировать весь спектр долговых стратегий государства. Технология анализа в данном случае такая же, как и при работе с уравнением (10). Из-за большого числа параметров, фигурирующих в (38), (40) и (41), подробное исследование долговых эффектов проводить не будем и ограничимся лишь общим видом найденных зависимостей. Отметим только в отношении соотношения (41), что оно на самом деле является весьма сложным и предполагает целую гамму условий, при которых динамика внешней задолженности может быть с течением времени ликвидирована. Вывод соответствующих условий достаточно прост, однако их громоздкость и количество не позволяют это проделать в рамках данной статьи. Сказанное автоматически предполагает и направление работы с моделью (41). Это прежде всего прогнозирование типа динамических траекторий yt0 с помощью проведения имитационных экспериментов. Здесь наибольший интерес представляет вопрос о том, через какой промежуток времени переменная внешнего долга y0 выйдет на требуемый уровень.
6. ПРАКТИЧЕСКАЯ ЗНАЧИМОСТЬ МОДЕЛЕЙ
Предложенные уравнения динамики внутренней и внешней государственной задолженности имеют как теоретическое, так и практическое значение. При этом теоретические и прикладные аспекты тесно переплетаются, что не позволяет рассматривать их автономно друг от друга. Наиболее значительным общеметодологическим результатом проведенного анализа является вывод о чрезвычайно низкой вероятности устойчивого функционирования экономических систем при сокращающейся государственной задолженности. Это в свою очередь свидетельствует об узости диапазона эффективных значений управляемых параметров, что диктует жесткие требования к монетарно-долговой и бюджетной политике государства.
Примечательно, что доказательство данного тезиса получено имитационно-аналитическим путем, то есть с помощью анализа математической структуры моделей динамики государственного долга и проведения экспериментальных расчетов для наиболее репрезентативных экономических режимов. Подобная схема исследования долговых стратегий восполняет имеющийся теоретический пробел в теории государственного сектора экономики, ибо ранее существовавшие подходы к обоснованию тенденции роста государственного долга базировались либо на чисто эмпирическом анализе соответствующих динамических рядов, либо на анализе специфики механизма функционирования финансовых институтов государства в демократических сообществах.
Несмотря на то, что построенные разностные модели динамики государственной задолженности могут быть уточнены и переработаны для макроэкономического прогнозирования, их широкое использование в чисто прогнозных целях вряд ли целесообразно. Наиболее эффективное применение моделей может быть достигнуто на стадии формирования и принятия конструктивных макрорешений и выработки общей линии в проведении долговой политики. Для этого при проведении модельных расчетов основной акцент должен быть сделан на получении качественной картины процесса.
Следует отметить наиболее интересные направления дальнейших количественных исследований. На наш взгляд, это прежде всего межстрановой анализ и исследование специфики национальных экономик с точки зрения наличия условий для реализации эффективной долговой политики. Было бы полезно оценить эффективные границы макроэкономических параметров, включая управляемые переменные, для таких стран, как США, Япония, Германия, а также для других развитых государств.
Основными потенциальными потребителями разработанного модельного инструментария являются федеральные ведомства в лице Министерства финансов, Министерства экономики и Центрального банка России. Оперативное отслеживание эффективных границ ключевых макропараметров позволит, на наш взгляд, вплотную приблизиться к синтезу системы государственного регулирования, включающей фискально-бюджетные и монетарно-долговые инструменты. В настоящее время практические макрорешения в указанных сферах являются почти полностью независимыми. Определенный интерес данный инструментарий представляет и для Министерства иностранных дел и Министерства внешних экономических связей России, которые могут использовать его в качестве аналитического аппарата по обоснованию целесообразности осуществления той или иной внешнеполитической стратегии.
ПРИЛОЖЕНИЕ
С учетом обозначений (42), (43) и (45) уравнение (39) перепишем в виде:

Распишем последовательные состояния для yt0 с учетом обозначения

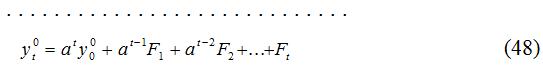
Таким образом, решением уравнения (46) является следующий ряд:

Константа
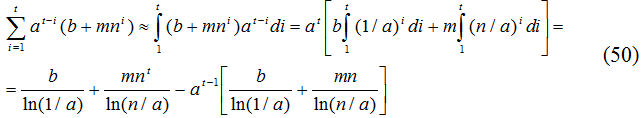
Оговоримся, что переход (50) правомерен лишь в пределе, когда временной шаг пренебрежимо мал. Однако при исследовании “длинных” временных траекторий подобный подход можно считать допустимым и для наших целей вполне приемлемым.
Подставляя (50) в (49) получаем функциональную зависимость (41), что и требовалось доказать.
- Е.В.Балацкий. Инфляционные налоги и экономический рост (“Экономика и математические методы”. Т.33. Вып.2, 1997).
- Е.В.Балацкий. Инфляционное равновесие и бюджетная сбалансированность (“Мировая экономика и международные отношения”. №3, 1997).
- Л.Е.Соколовский. Финансирование бюджетного дефицита и внутренний государственный долг (“Экономика и математические методы”. Т.27. Вып.2, 1991).
- Г.Корн, Т.Корн. Справочник по математике для научных работников и инженеров. М., 1984.
- А.А.Миролюбов, М.А.Солдатов. Линейные неоднородные разностные уравнения. М., 1986.
- Е.В.Балацкий. Издержки и полезность как факторы ценообразования (“Вестник Московского университета. Серия 6, Экономика”. №4, 1996).
- Л.Харрис. Денежная теория. М., 1990.
- Н.М.Травкина, В.С.Васильев. Апокалипсис современных экономических систем: “зверь” из бюджета (“США - экономика, политика, идеология”. №2, 1994).
- А.Б.Аткинсон, Дж.Э.Стиглиц. Лекции по экономической теории государственного сектора. М., 1995.
- Е.В.Балацкий. Регулирование занятости в свете теории мультипликатора (“Мировая экономика и международные отношения”. №4, 1996).
- И.Н.Бронштейн, К.А.Семендяев. Справочник по математике для инженеров и учащихся втузов. М., 1986.
- В.Н.Сумароков. Государственные финансы в системе макроэкономического регулирования. М., 1996.
- V.V.Roley. A Theory of Federal Debt Management (“The American Economic Review”. No.5. Vol.69, 1979).
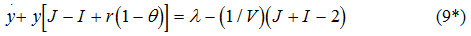
Ее решением является функция
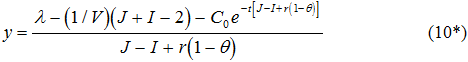



































Написать комментарий
Проблема обслуживания государственного внешнего долга - один из ключевых факторов макроэкономической стабильности в стране. От характера решения долговой проблемы будет зависеть бюджетная дееспособность России, состояние ее валютных резервов, а, следовательно, стабильность национальной валюты, уровень процентных ставок, инвестиционный климат, характер поведения всех сегментов отечественного финансового рынка. Практически все страны мира, проводя экономические преобразования, прибегают к внешним источникам финансирования. Рациональное использование иностранных займов, кредитов и помощи способствует ускорению экономического развития, решению социально-экономических проблем. Однако отсутствие целостной государственной политики по привлечению и использованию внешних финансовых ресурсов ведет к образованию внешней задолженности, которая становится серьезным препятствием на пути экономических преобразований. Экономические события последних лет, обусловили переход вопросов управления государственным долгом в разряд первостепенных. Более того, можно с уверенностью утверждать, что данная тема будет оставаться важнейшим предметом для обсуждения и в ближайшей перспективе. С макроэкономической точки зрения все государственные расходы делятся на: государственные закупки товаров и услуг (их стоимость включается в ВВП); трансферты (их стоимость не включается в ВВП); выплаты процентов по государственным облигациям (обслуживание государственного долга).