Что такое точки Лаффера? Какова их роль для национальной экономики? Как можно определить количественно величину этих пресловутых точек? Какими свойствами обладают эти аналитические объекты? Как с ними следует работать? Какие выводы можно сделать, опираясь на их анализ?
Существует множество работ, посвященных исследованию лафферовых эффектов [1-7]. Несмотря на это до сих пор не предложено удовлетворительной методики оценки точек Лаффера, особенно применительно к макроситуации. Большинство работ оперирует либо микроконструкциями, не позволяющими выйти на уровень макрообобщений, либо использует плохо верифицируемые параметры, слабо приспособленные к существующей статистической отчетности. Предполагаемые в некоторых работах методы в инструментальном плане достаточно сложны и, следовательно, мало пригодны для практических макрорасчетов. Кроме того, абсолютное большинство экономистов в своих разработках опирается на оптимизационную идеологию, которая, как было показано в [7], чревата высокой степенью субъективности получаемых оценок. Вместе с тем нынешнее состояние российской экономики выдвигает задачу определения точек Лаффера, которая не может быть решена без создания соответствующего методического аппарата. Целью данной статьи будет построение дескриптивной модели, воспроизводящей процесс формирования фискальных платежей в инфляционной среде, и разработка численного алгоритма отыскания точек Лаффера.
1. ДЕСКРИПТИВНАЯ МОДЕЛЬ ФОРМИРОВАНИЯ ФИСКАЛЬНЫХ ДОХОДОВ ГОСУДАРСТВА
Анализ литературы по теории налогов показывает, что практически все экономисты, пытавшиеся оценить точки Лаффера, культивируют оптимизационные модели. Однако все построения подобного рода весьма уязвимы как с теоретических, так и с практических позиций (критические тезисы по этому поводу приводятся в [7]). Мы же будем пропагандировать принципиально иной подход, основанный на дескриптивной модели, воспроизводящей поведенческие свойства экономической системы. Насколько нам известно, такая концептуальная линия применительно к теории налогов будет проводиться впервые.
Так как все современные экономические системы функционируют в инфляционном режиме, то мы будем полагать, что основным фактором, определяющим все экономические процессы, является рост цен. При этом каждый конкретный экономический режим характеризуется определенным набором показателей эластичности. В нашем случае будут рассмотрены эластичности основных макропоказателей по ценам. Конкретизируем сказанное.
Для обозримости всех модельных построений ограничимся тремя видами налогов: на добавленную стоимость, прибыль и заработную плату. В этом случае общая масса налоговых сборов складывается из трех составляющих фискальных платежей:
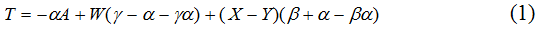
Предположим, что все рассматриваемые агрегаты T, A, W, X и Y зависят от уровня цен P. Тогда уравнение (1) можно переписать в форме эластичностей с учетом сложившейся народнохозяйственной структуры затрат:
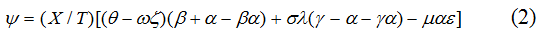
Учитывая, что
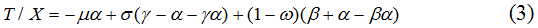

Выведенное дифференциальное уравнение (4) представляет собой дескриптивную модель формирования бюджетных доходов в инфляционной обстановке с учетом сложившейся производственной структуры затрат.
Введем в рассмотрение фискально-ценовой коэффициент k:
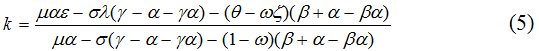
Фискально-ценовой коэффициент определяет величину эластичности налоговых сборов по ценам. Если все параметры эластичности и структурные показатели затрат постоянны, то решением (4) является следующая степенная функция:

Так как одним из факторов, ведущих к росту налоговых сборов, в нашем случае являются цены, то в дальнейшем будем рассматривать реальные (продефлированные) налоговые поступления

Коротко прокомментируем основные посылки дескриптивной идеологии, которая была нами использована при выводе зависимости (7). Дело в том, что в традиционных оптимизационных моделях фискальный эффект от увеличения ставок налогов расщепляется на два субэффекта: первый показывает влияние налоговых ставок на производственную активность экономики, второй - влияние роста производства на объем фискальных сборов [7]. Особые трудности вызывает оценка первого субэффекта. В нашем же случае оба субэффекта сливают в один, который и подлежит непосредственной оценке. Реакция производства на изменение экономических условий здесь также присутствует, но в модифицированном, скрытом виде и отображается показателями эластичности: θ, ζ, λ и ε. Таким образом, нами неявно предполагается, что на производственные стратегии предприятий влияют прежде всего ценовые сдвиги, а не изменения налоговых ставок.
Действительно, в результате варьирования налоговых ставок, как правило, меняется ценовая картина на экономических рынках, вслед за чем уже происходит пересмотр объемных показателей выпуска и затрат. Следовательно, фискальные импульсы сказываются на производственных параметрах опосредованно - через ценовые эффекты. Такой подход, на наш взгляд, даже предпочтительнее, чем традиционные, так как он внутренне более “динамичен”. Однако совершенно очевидно и то, что в общем случае изменения налогового климата могут вызывать не только сдвиги в уровне цен, но и в величине эластичностей θ, ζ, λ и ε. Данный факт нами не учитывается, и это является единственным существенным допущением предложенной методики анализа фискальных эффектов. Тем не менее представляется, что сформулированный постулат не является слишком уж абстрактным, так как для реальной экономики всегда характерна некоторая инерционность и консервативность в формировании той или иной реакции на рост цен. Кроме того, сама реакция выпуска на ценовые колебания является вообще вторичной по отношению к реакции спроса, так как именно спрос является верхним потолком для роста производства. Для статического анализа, включая метод сравнительной статики, который предполагает мгновенные изменения всех переменных, введенная нами посылка является тем более правомерной.
Таким образом, нами рассматривается экономическая система, пронизанная в каждый момент времени постоянно происходящими ценовыми импульсами. Ужесточение налоговых условий в лишь подстегивает инфляцию, которая в свою очередь и предопределяет все производственные характеристики. Для упрощения анализа будем полагать, что инфляционные тенденции носят автономный характер и обусловлены монетарной политикой государства.
2. АЛГОРИТМ ОТЫСКАНИЯ ТОЧЕК ЛАФФЕРА
Чтобы разобраться в специфике образования точек Лаффера, рассмотрим сначала простейший случай, когда в зависимости (7) изменяется только один налоговый параметр. Для определенности пусть это ставка налога на добавленную стоимость. Для случая k>1 из (7) легко получить условие, при котором
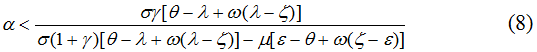
Аналогичная ситуация характерна и для ставки налога на прибыль. Для этого налога
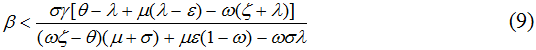
Из (8) и (9) видно, что в стабильной ценовой среде классический эффект Лаффера не проявляется и, соответственно, точка Лаффера отсутствует. Однако, как будет показано выше, ситуация в корне меняется, когда сдвиг налоговой ставки происходит на фоне ненулевой инфляции.
Рассмотрение условий (8) и (9) само по себе весьма полезно, так как последние показывают направленность возможных изменений объема налоговой массы при увеличении таких двух значительных фискальных инструментов, как налоги на прибыль и добавленую стоимость. Вместе с тем анализ автономного действия налоговых ставок является явным упрощением ситуации, так как в реальности воздействие активной фискальной политики “накладывается” на перманентный рост цен, который также изменяет величину как номинальных, так и реальных налоговых поступлений. Это особенно актуально в периоды высокой инфляции.
Чтобы определить совместное влияние роста цен и увеличения налоговой ставки (для определенности и наглядности ограничимся налогом на добавленную стоимость) необходимо рассмотреть поведение величины дифференциала dT0:

Введя обозначение темпа прироста цен ρ=dP/P и учитывая, что

Из (10) и (11) вытекает, что при ρ>0,

В целом, усиление инфляции действует в направлении “выталкивания” точки Лаффера за область допустимых значений и в соответствии с (13)

Таким образом, для экономики, находящейся на высокоинфляционной траектории, бессмысленно говорить об эффектах Лаффера и точках Лаффера, ибо таковых просто не существует. Мы полагаем этот вывод принципиальным, так как он проясняет одно из важнейших функциональных свойств экономической системы.
Рассмотренный случай k>1 можно считать типичным. Однако, как следует из (11), в такой ситуации точка Лаффера находится всегда правее фактической ставки налога, как это показано на рис.2. Однако совершенно очевидно, что в общем случае модель (4) должна предусматривать и такие случаи, когда точка Лаффера сдвинута влево от фактической ставки (см. рис.2). Анализ показывает, что такая ситуация действительно возможна при k<1. Подобный экономический режим можно считать аномальным, хотя и полностью исключить его нельзя. При k<1 точка Лаффера существует как и в предыдущем варианте только при

Соответственно корректируются формулы (12) и (13):


Таким образом, мы получили простой алгоритм определения точек Лаффера, который может быть выражен следующей четырехшаговой процедурой:
- точка Лаффера может существовать только при
- точка Лаффера превышает реально действующую ставку налога при k>1 и, наоборот, точка Лаффера ниже фактической ставки при k<1. Следовательно, следующий шаг вычислений предполагает оценку величины k. В ряде случаев, когда достаточно иметь только качественное представление о месторасположении точки Лаффера, расчетом значения k можно удовлетвориться и последующие вычисления не проводить.
- непосредственная величина точки Лаффера получается по формуле (11) для k>1 и по формуле (14) для k<1. Анализ показывает, что формула (11) по сути универсальна и работает в обоих случаях с учетом знака выражения, стоящего под логарифмом.
- точка Лаффера должна удовлетворять априорным ограничениям. Это означает, что значимость точки Лаффера может быть определена только, если β0<1 для случая k>1 и если β0>1 для случая k<1. При нарушении данных ограничений точка Лаффера лежит за пределами области допустимых значений, что в содержательном отношении равносильно ее отсутствию.
Вспомогательная формула для расчета ∂k/∂β получается из (5) и имеет вид:
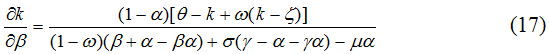
В заключение остановимся подробнее на том, насколько насыщенной является построенная модель (4) с точки зрения отображения лафферовых эффектов. Так, например, формула (11) позволяет выявить модифицированные автономные точки Лаффера 2-го рода (точки Лаффера 1-го рода моделью (4) вообще не затрагиваются; подобные фискальные эффекты находятся вне условий нашей аналитической схемы). Модификация автономных точек заключается во введении в рассмотрение инфляционной составляющей; без учета инфляционного фактора традиционные (в смысле [7]) точки Лаффера не проявляются. В этом смысле модель (4) представляет собой незначительное упрощение традиционных оптимизационных схем анализа. Что касается синхронных точек Лаффера, то здесь модель (4) дает классический результат. Так, например, если возмущения идут со стороны налога на добавленную стоимость и налога на прибыль, то из (4) автоматически получается пара точек Лаффера (α**;β**), которая определяется из условий (8) и (9), преобразуюшиеся в данном случае в строгие равенства. При этом полученные точки заведомо являются точками Лаффера, так как выход за них ведет к изменению знака производных ∂T/∂α и ∂T/∂β с “+” на “-”. При этом само существование синхронных точек Лаффера является безусловным, то есть не требует рассмотрения ценовых сдвигов. Иными словами, точки Лаффера, определяемые из соотношений (11) и (14), могут считаться динамическими, так как требуют ценовой нестабильности, в то время как синхронные точки (α**;β**) являются статическими, ибо возникают даже при фиксированных ценах.
Таким образом, построенная модель (4) в достаточно полной мере аккумулирует лафферовы эффекты и в целом ничем не уступает оптимизационным моделям теории налогов.
3. АПРОБАЦИЯ МЕТОДА
Проверим работоспособность предложенного метода для оценки точек Лаффера на российских данных. Исходной информацией для расчетов являются таблицы 1-3. Показатели эластичности нами оценивались грубым способом как отношение темпов прироста. Так, например, для θ использовалась формула:
| Доля в валовом общественном продукте | 1991 | 1992 | 1993 | 1994 | 1991-1994 |
|---|---|---|---|---|---|
| оплаты труда (σ) | 18,66 | 10,49 | 13,88 | 12,55 | 13,90 |
| материальных затрат (ω) | 52,24 | 58,59 | 51,00 | 58,59 | 55,11 |
| амортизации (μ) | 8,21 | 4,70 | 7,90 | 5,10 | 6,48 |
| Эластичность | 1991-1992 | 1992-1993 | 1993-1994 | 1991-1994 |
|---|---|---|---|---|
| выпуска по ценам (θ) | 0,68 | 0,72 | 1,23 | 0,88 |
| оплаты труда по ценам (λ) | 0,31 | 0,99 | 1,07 | 0,79 |
| материальных затрат по ценам (ζ) | 0,73 | 0,61 | 1,48 | 0,700,94 |
| амортизации по ценам (ε) | 0,70 | 1,29 | 0,63 | 0,87 |
| Сценарий расчета | Ставки налога на | ||
|---|---|---|---|
| прибыль (α) | добавленную стоимость (β) | заработную плату (γ) | |
| №1 | 20,0 | 20,0 | 41,0 |
| №2 | 20,0 | 20,0 | <41,0/td> |
В соответствии с нашим алгоритмом отыскания точек Лаффера оценим сначала реакцию фискальных доходов на изменение налоговой ставки. В качестве последней как и ранее ограничимся ставкой налога на добавленную стоимость. В соответствии с (4) для k<1 имеет место формула

К сожалению российские данные не позволяют в полной мере оценить возможности, заложенные в представленной выше вычислительной схеме. В конкретных расчетах нами использовался усредненный вариант экономических параметров россиской экономики за период времени 1992-1994 гг., так как по отдельным годам они были подвержены сильным флуктуациям. При этом, как показали расчеты, оба сценария таблицы 3 практически ничем не отличаются. Вычисления указывают на то, что в том и другом случае k=0,8, то есть каждый процент инфляции приводил к росту реальных фискальных доходов только на 0,8%, а незначительные вариации величин прочих налоговых ставок (в нашем случае налога на прибыль) не могли кардинально изменить фискально-ценовой климат. Таким образом, можно сделать вывод, что инфляция 1991-1994 гг. была крайне невыгодна российскому бюджету, ибо при сложившейся производственной структуре затрат и реакции производства на ценовые сдвиги доходы государства отставали от роста цен. В этих условиях эффект
Из сказанного напрашивается вывод, что в коллапсирующей экономике, каковой являлась российская экономика 1991-1994 гг., существование автономной точки Лаффера является весьма проблематичным. Разумеется, это не означает принципиальной невозможности появления точки Лаффера в кризисных условиях. Однако в этом случае глубина стагфляционных “ям” не должна быть чрезмерной.
Что касается синхронных точек Лаффера, определяемых из (8) и (9), то в соответствии с расчетами таковые также отсутствуют, что подтверждает вывод о сложной фискальной обстановке, сложившейся в российской экономике переходного периода. Конкретизируя сказанное укажем, что получившиеся оценки пары синхронных точек Лаффера (α**;β**) свидетельствует об их явной вырожденности: (α**=?75,5%; β**=43,6%). Отрицательность критической ставки налога на прибыль, на наш взгляд, свидетельствует об отсутствии рациональной системы налогообложения для “падающей” экономики России.
4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Рассмотрим более подробно некоторые методологические аспекты, связанные с практическим применением предложенного алгоритма по отысканию точек Лаффера.
Прежде всего коснемся специфики информационного обеспечения численного метода. Во-первых, чтобы получить оценки структурных показателей затрат и эластичностей необходимы данные третьего квадранта отчетных межотраслевых балансов, очищенные от налоговых выплат. Во-вторых, необходимы данные о темпах инфляции. Для этого следует определить показатель-дефлятор, который будет использоваться в расчетах. Данный момент достаточно важен, так как некорректные дефляторы приведут к смещению всех оценок вплоть до принципиального искажения истинной картины процесса.
При подготовке исходной информации следует также стремиться, чтобы все данные были сопоставимыми. Так, например, все параметры вычислительной схемы могут оцениваться на базе как среднемесячных, так ежеквартальных и среднегодовых данных. Особо следует следить за тем, чтобы была обеспечена временная однопорядковость показателей эластичности и темпа инфляции. На наш взгляд, предпочтение стоит отдавать годовой отчетности как более репрезентативной и устойчивой во времени.1
Относительно методов расчета эластичностей. Здесь возможны два подхода. Первый базируется на построении эконометрических зависимостей между объемами (или темпами роста) производственных затрат и цен. Такой способ предполагает наличие достаточно длинных динамических рядов и при удовлетворительных статистических параметрах регрессионных зависимостей дает хорошие результаты. Однако в ряде случаев длина ретроспективных рядов может быть недостаточной (что, кстати говоря, характерно для российской экономики переходного периода), а межвременные перепады в данных слишком значительными. В этом случае можно воспользоваться вторым подходом к оценке эластичностей, который предполагает исчисление отношения соответствующих темпов прироста в дискретной форме, то есть для каждого малого временного интервала получаются индивидуальные оценки эластичностей. Именно этим подходом мы пользовались в наших расчетах. Так как подобный “интервальный” способ является грубым, то на практике следует по возможности усреднять получаемые с его помощью оценки.
Теперь проанализируем некоторые побочные теоретические аспекты предложенного метода. В частности, автономные точки Лаффера получаются из условия (10) и предусматривают изменение только одного вида налога. На практике возможна ситуация, когда оказываются задействоваными несколько налогов. Тогда, например, для налога на прибыль и налога на добавленную стоимость условие для определения точки Лаффера примет вид:
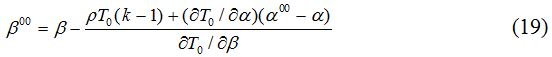
В этом случае точка Лаффера β00 зависит от изменения налоговой ставки α и может называться условной точкой Лаффера. Такого рода точки Лаффера возникают только при реализации дескриптивной схемы анализа, которую мы избрали в начале. В целом, методология нашего анализа может быть охарактеризована как дескриптивно-квазидинамическая в отличие от традиционной оптимизационно-статической. Как было показано выше, возможности дескриптивно-квазидинамической идеологии значительно шире. В частности, только в ее рамках появляются условные точки Лаффера типа (19). Вместе с тем, на наш взгляд, при разработке макрополитики фискального регулирования реальную значимость приобретают прежде всего условные точки Лаффера. Более того, вычислительная схема типа (19) открывает интересные возможности в отношении макропрогнозирования и проведения вариантных расчетов по согласованию монетарной и фискальной стратегий государства.
Соотношение между автономной точкой β0 и условной точкой β00 вытекает из (11) и (19):

Теперь взглянем на полученную фискальную зависимость (6) с точки зрения ее соответствия некоторым априорным условиям. Так, например, классическая кривая Лаффера обладает такими свойствами, как наличие строгих граничных условий, а именно: Т(0)=0; Т(1)=0. В этой связи возникает два взаимосвязанных вопроса. Первый: насколько наша фискальная кривая (6) удовлетворяет априорным граничным условиям и, следовательно, как хорошо она вписывается в классический фискальный анализ? Второй: насколько вообще реалистична и выполнима такая жесткая закрепленность кривой Лаффера на обоих концах?
В соответствии с (6) при всех налоговых параметрах, стремящихся к 0 и 1, имеем:
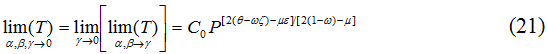

Таким образом, ни одно из априорных граничных условий для дескриптивной модели (4) не выполняется и в этом заключается один из ее серьезных минусов. Так как (6) генерирует ненулевые значения налоговых сборов на фискальных полюсах, то, видимо, и сама вычислительная процедура будет давать хорошие результаты только тогда, когда фискальные параметры находятся ближе к середине шкалы аргумента; при приближении параметров к своим границам метод может давать сильные погрешности. Вид кривой Лаффера, которая может иметь место в соответствии с (21) и (22), показан на рис.3; в зависимости от выполнения или невыполнения неравенства зависит какой из концов фискальной кривой выше. Таким образом, в соответствии с (21) и (22) кривая Лаффера асимметрична.
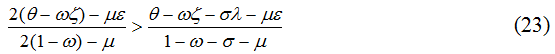
Несколько слов по поводу второго вопроса. Дело в том, что несмотря на кажущуюся очевидность, лафферовы граничные условия являются совершенно противоестественными и представляют собой лишь некую гипотетическую абстракцию. Так, например, равенство всех налоговых ставок нулю означает отсутствие самой налоговой системы, а, следовательно, и государства, неотъемлемым атрибутом которого она является. Как справедливо отмечал Р.Барр, не существует экономической политики без политики общей и нет политики вообще, если нет государства [8]. Хотя в этой ситуации сумма налогов и будет формально равна нулю, само ее наличие абсолютно нереалистично и сказать что-либо о закономерностях функционирования такой системы просто нельзя.
Другой крайний случай, когда все налоги завинчены до упора, представляется не менее вырожденным. Однако даже если такое и возможно, то отнюдь не факт, что производство полностью свернется, а государство ничего не получит в виде налогов. Бывшие социалистические страны с централизованной экономикой практиковали нечто подобное, тем не менее производственный сектор в них так или иначе развивался, а государство исправно собирало налоги и пополняло свой бюджет.
Из сказанного вытекает, что исследование лафферовых эффектов должно проводиться не на всей налоговой шкале [0;1], а на значительно более узком, усеченном отрезке; на концах шкалы все свойства экономической системы оказываются размытыми и неопределенными. Это в свою очередь означает, что нарушение априорно заданных граничных условий вряд ли может служить доказательством серьезных изъянов в сконструированной нами модели (4). Заметим, что даже оптимизационные постановки задачи приводят к нарушению канонических граничных свойств кривой Лаффера. Так, например, в [5] налоговые поступления обнуляются на правом конце фискальной кривой, лежащем значительно ближе единичной отметки.
5. НАПРАВЛЕНИЯ ИСПОЛЬЗОВАНИЯ МЕТОДА
В данной работе мы ограничились самыми общими расчетами точек Лаффера по предложенной схеме. При этом оказалось, что Россия в предыдущие кризисные годы имела экономические характеристики, чрезвычайно “невыгодные” для нашего анализа. Однако отсутствие лафферовых эффектов для российской экономики еще не означает малопродуктивность разработанного вычислительного алгоритма. В этой связи, по-видимому, подобные расчеты целесообразно продолжать, так как по мере стабилизации экономической ситуации в России возрастает вероятность “проявления” лафферовых эффектов, которые и могут быть своевременно выявлены с помощью нашего метода. Однако и сейчас имеются интересные направления дальнейших количественных исследований. На наш взгляд, это прежде всего межстрановой анализ и исследование специфики национальных экономик. Было бы в высшей степени интересно и полезно оценить точки Лаффера для различных видов налогов на примере США, Японии, Германии и других стран с мощным экономическим потенциалом.
Особого внимания заслуживает вопрос о том, какой из ныне существующих методов оценки точек Лаффера следует выбрать в качестве “главного”, который в дальнейшем мог бы получить статус “официального”. Представляется, что все они должны какое-то время находиться в состоянии мирного сосуществования, но ожесточенной конкуренции. Предпочтение должно отдаваться все же дескриптивным схемам, которые объективно воспроизводят функциональные свойства системы, нежели оптимизационным, использующим конкретные финансовые критерии эффективности деятельности экономических агентов [7].
Основными потенциальными потребителями разработанного инструментария являются федеральные ведомства в лице Министерства финансов, Министерства экономики и Центрального банка России. Оперативное отслеживание предельно допустимых налоговых ставок в совокупности с темпами инфляции, выпуска и производственных затрат позволяет вплотную приблизиться к макроэкономическому синтезу фискальной и монетарной политики государства, которые в настоящее время почти полностью “отъединены” друг от друга.
- С.В.Алексашенко, Д.А.Киселев, П.М.Теплухин, Е.Г.Ясин. Налоговые шкалы: функции, свойства, методы управления (“Экономика и математические методы”. Т.25. Вып.3. 1989).
- Л.Е.Соколовский. Подоходный налог и экономическое поведение (“Экономика и математические методы”. Т.25. Вып.4. 1989).
- Л.Е.Соколовский. Налог на добавленную стоимость и предприятие, максимизирующее прибыль (“Экономика и математические методы”. Т.28. Вып.4. 1992).
- С.М.Мовшович, Л.Е.Соколовский. Выпуск, налоги и кривая Лаффера (“Экономика и математические методы”. Т.30. Вып.3. 1994).
- В.В.Капитоненко. Инфляционный сдвиг налоговой ставки на кривой Лаффэра (“Экономика и технология: межвузовский сборник научных трудов”. М.: 1994).
- С.В.Гусаков, С.В.Жак. Оптимальные равновесные цены и точка Лаффера (“Экономика и математические методы”. Т.31. Вып.4. 1995).
- Е.В.Балацкий. Лафферовы эффекты и финансовые критерии экономической деятельности (“Мировая экономика и международные отношения”. №11. 1997).
- Р.Барр. Политическая экономия. Т.1. М.: 1995.



































Написать комментарий