Факторы формирования валютных курсов: плюрализм моделей, теорий и концепций

Хорошо известно, что валютный климат в стране оказывает огромное влияние на национальную экономику. В связи с этим неудивительно, что экономисты с давних пор пытаются понять законы, в соответствии с которыми происходит формирование валютных курсов национальных денежных единиц. Знание этих законов позволило бы прогнозировать динамику валютных курсов, а это в свою очередь помогло бы государству предотвращать кризисные ситуации в развитии экономики, а отдельным экономическим агентам – минимизировать хозяйственные потери. Однако проблема заключается в том, что искомые законы так и остаются скрытыми от нас, а вместо них имеются многочисленные теории, модели и концепции, позволяющие лишь слегка приблизиться к пониманию движущих сил формирования валютных курсов.

На наш взгляд, в настоящее время назрела проблема анализа накопленного аналитического арсенала в данной области. Это связано, по крайней мере, с двумя причинами. Во-первых, за последние годы (за последние примерно 10-15 лет) экономисты дополнительно продвинулись в понимании факторов валютной динамики. Во-вторых, до сих пор достаточно полного обзора разработок в данной области нет, в то время как практические задачи по прогнозированию валютных курсов требуют знания всего спектра экономических факторов, влияющих на их динамику. В данной статье попытаемся восполнить образовавшийся пробел в области так называемого фундаментального анализа; методы технического анализа выходят за рамки нашего исследования.

1. Теория абсолютного паритета покупательной силы. Основоположником данной теории считается Г.Кассель, обобщивший аналогичные разработки Д.Рикардо [1, с.66]. В соответствии с ней валютный курс определяется соотношением уровней цен в рассматриваемых странах:

Соотношение (1) предполагает действие так называемого «закона одной цены», согласно которому цены на товары в одной стране равны ценам на товары в другой стране [2, с.48].

Формула (1) отражает закон формирования валютного курса в статике. Однако этот закон может быть легко переведен в динамическую форму:

Многие аналитики подчеркивают, что закон одной цены в чистом виде выполняется только при наличии идеального равновесия во внешнеторговой сфере страны (торговый баланс должен быть равен нулю [1, с.67]). Как правило, это условие нереалистично. Попытки эмпирической проверки теории абсолютного паритета покупательной силы (способности) показали ее неоднозначность. С одной стороны, в целом эта теория не подтверждается, с другой – на определенных исторических участках развития она соответствует реальности. В частности, Я.Френкел оценил коэффициенты регрессионного уравнения k = α(P / P₀)σ, где α и σ – параметры регрессии. Результаты расчетов на основе ежемесячной статистики валютных курсов и оптовых цен с февраля 1921 г. по май 1925г. показали, что курсы немецкой, французской, английской и американской валют в основном подчинялись закону абсолютного паритета покупательной силы (1) [1, с.67-68].

В настоящее время специалисты сходятся во мнении, что закон одной цены (1) выполняется лишь в долгосрочном аспекте [1, с.69]. Действительно, сбои в «работе» данного закона приводят к несовпадению номинальных и реальных (дефлированных) валютных курсов, причем на одних участках времени номинальный курс оказывается выше реального, а на других – ниже [2, с.51-53]. Однако, как было указано выше, в ряде случаев указанный закон все же может эффективно использоваться и для исследования краткосрочных эффектов. Таким образом, теория абсолютного паритета покупательной силы (ППС) не может быть отброшена и должна использоваться как в теоретических, так и практических исследованиях. Вместе с тем ее применение в «автономном режиме» требует большой осторожности.

2. Теория относительного паритета покупательной силы. Данная теория также берет начало с работ Г.Касселя и утверждает, что валютный курс определяется не столько абсолютными ценами, сколько их относительными изменениями [2, с.49]:

Если в качестве k(0) в модели (3) использовать номинальный валютный курс в начальный момент времени, то и само соотношение (3) будет всего лишь динамическим аналогом уравнения (1). Таким образом, если не привязываться к каким-то особым схемам расчета равновесного курса в (3), то теории абсолютного и относительного паритета покупательной силы следует признать эквивалентными. По-видимому, именно этим фактом и обусловлен факт редкого упоминания в научной литературе теории относительного паритета покупательной силы.

3. Монетаристская версия теории абсолютного паритета покупательной силы. Вводя гипотезу монетаризма о том, что темпы инфляции определяются темпом роста денежной массы, уравнение (2) можно переписать в следующем виде [3, с.166]:

Фактически формула (4) и представляет собой квинтэссенцию монетаристской версии теории абсолютного паритета покупательной силы, хорошо известную в финансовой теории.

Надо сказать, что если модель (1) имеет ограниченную область применения, то модель (4) представляется еще более условной. Это особенно отчетливо проявляется для случая, когда одна из рассматриваемых валют является лишь внутренне конвертируемой. Типичными образчиками подобной ситуации могут служить российский рубль и израильский шекель [3, с.165]. В подобной ситуации более правомерна следующая версия (4):

В основе модели (5) лежит положение том, что вместо темпа роста всей иностранной денежной массы следует рассматривать темп роста иностранной валюты, располагаемой агентами внутреннего рынка. Действительно, было бы совершенно абсурдно привязывать курс «рубль/доллар» к росту общемировой долларовой массы. Значительно более логично привести привязку к долларовой массе, циркулирующей в экономике России, что и предполагает уравнение (5). Вместе с тем совершенно очевидно, что такая модификация исходной монетарной модели (4) по сути дела означает принципиальный пересмотр самого денежно-ценового механизма формирования валютных курсов.

Надо сказать, что монетаристские модели (4) и (5) теории покупательной силы следует признать не просто упрощенными, но и заведомо примитивными. В частности, при переходе от уравнения (2) к (4) игнорируется так называемое уравнение И.Фишера PX=VM, где X – объем товарной массы в экономике страны (в неизменных ценах); V – скорость обращения денег; остальные обозначения прежние. Для «внешней» экономики, к валюте которой котируется национальная денежная единица, можно записать аналогичное уравнение: P₀X₀ = V₀M₀. Тогда уравнение (2) можно записать в следующем виде:

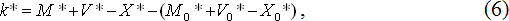
Несложно видеть различие между уравнениями (4) и (6). Из их сопоставления вытекает, что монетаристская версия теории паритета покупательной силы по умолчанию предполагает равенство: V*-X* = V₀*-X₀*. Данное условие заведомо выполняется при постоянстве объемов производства и скорости обращения денег в обеих странах. Фактически именно эта предпосылка и лежит в основе модели (4). Однако игнорирование таких двух макроэкономических параметров для обеих рассматриваемых стран лишь в очень редких случаях может быть оправданным. По-видимому, именно в этом и заключается основной изъян монетаристской теории паритета покупательной силы.

В защиту данной теории можно сказать лишь одно: как правило, в чистом виде эта теория на практике не используется. Но тогда возникает логичный вопрос: тогда зачем она вообще нужна? Наш ответ на данный вопрос таков: данная теория используется в качестве исходной точки для построения более адекватных и конструктивных моделей. Действительно, как методологическая база монетарная теория формирования валютных курсов очень удобна, чем и обусловлена ее ценность и значимость. Полностью отбросив ее, мы, по всей вероятности, потеряли бы целый ряд важных и интересных модельных схем.

4. Неравновесная теория абсолютного паритета покупательной силы. Краеугольным камнем теории абсолютного ППС является уравнение (1), представляющее собой некое условие ценового равновесия. Между тем простейшие расчеты показывают, что подобное равновесие наблюдается довольно редко. Следовательно, на практике мы в основном сталкиваемся с ситуацией отклонения от равновесия. Логичным шагом в учете данного факта является переход к рассмотрению неравновесных схем формирования валютных курсов на основе паритета покупательной силы.

Одной из наиболее простых и конструктивных моделей такого рода можно считать модель А.А.Первозванского [3]. Рассмотрим ее более подробно.

Первое уравнение модели имеет следующий вид [3, с.166]:

Несложно видеть, что данное выражение представляет собой нечто среднее между уравнениями (2) и (5). Фактически в монетаристской модели (5) произведена замена темпа роста денежной массы на темп инфляции и тем самым как бы осуществлен возврат к традиционной теории ППС. Таким образом, сама модель (7) может квалифицироваться как «полумонетаристская» концепция формирования динамики валютного курса. Уже на этом этапе построения модели видна ее определенная эклектичность, что можно смело отнести к числу ее минусов.

Второе уравнение модели задает простейшую линейную зависимость темпа поступления в страну иностранной валюты от степени расхождения валютного курса и ППС [3, с.166]:

В соответствии с логикой (8) при k(t) > P(t) / P₀(t) стимулируется экспорт и, следовательно, приток иностранной валюты в страну; в противном случае стимулируется импорт и происходит утечка иностранной валюты.

Если ввести в рассмотрение относительный коэффициент валютного неравновесия Ω(t) = k(t)P₀(t) / P(t) и принять гипотезу о неизменности цен во «внешней среде», т.е. об отсутствии инфляции в стране-носителе иностранной валюты, то подстановка соотношения (8) в (7) даст следующую редуцированную модель:

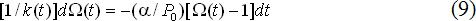
Модель (9) представляет собой обыкновенное дифференциальное уравнение, описывающее динамику коэффициента валютного неравновесия. Следовательно, и сама модель (7)-(8) представляет собой формальную схему неравновесной концепции ППС.

Как в большинстве экономических моделей, уравнение (9) основано на предпосылке стремления системы к равновесию. В соответствии с ним любое нарушение ценового паритета «включает» механизм перелива иностранной валюты, направленный на восстановление паритета. Безусловно, такой взгляд на природу валютных курсов значительно ближе к реальности, чем равновесная теория ППС.

Какова же практическая ценность неравновесной модели ППС (7)-(8)? Может ли она служить в качестве достойного заменителя всевозможным аранжировкам равновесной теории ППС?

Решение уравнения (9) можно записать в следующем виде [3, с.166]:

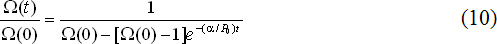
Полученная логистическая кривая (10) позволяет оценить скорость движения системы к равновесию, т.е. Ω(t) → 1. Расчеты показали, что тенденция, имевшая место в России в переходный период, довольно хорошо вписывается в теоретическую траекторию (10). Так, возникшее в первоначальный момент неравновесие между валютным курсом «рубль/доллар» и соответствующим ППС постепенно уменьшалось. Тенденция постепенной сходимости процесса к ценовому паритету очевидна из анализа динамики коэффициента неравновесия (Ω) за период 1992-1995 гг.: 11,5; 3,7; 3,1; 1,9 [3, с.167].

Идентификация параметров модели (10) позволила также А.А.Первозванскому сделать следующий прогноз: приближение валютного курса «рубль/доллар» к паритету с точностью до 5% произойдет к 2005 г. [3, с.167].

Все сказанное подводит к недвусмысленному пониманию, что если равновесные схемы ППС более или менее работоспособны в условиях стабильных экономических и валютных систем, то для формирующихся, «молодых» экономик они совершенно не пригодны. Для последних более приемлемыми оказываются неравновесные модели ППС типа (7)-(8). Вместе с тем, как справедливо подчеркивал А.А.Первозванский, такие модели носят тоже крайне упрощенный характер, и в лучшем случае могут использоваться в качестве теоретической схемы для «объяснения» происходящих событий на определенном отрезке экономического развития, но ни в коем случае не для осуществления численных прогнозов [3, с.167]. Надо сказать, что российский валютный кризис 1998 г. с мгновенной 4-кратной девальвацией рубля «разорвал» установившуюся довольно гладкую тенденцию к сближению валютного курса и ППС. Данный факт лишний раз продемонстрировал ограниченность не только равновесных теорий ППС, но и их неравновесных модификаций.

1. Концепция маржинальной эффективности внешнеторговых операций. Данная концепция была развита в работах С.Н.Журавлева в 1990-1992 гг. [4-6]. В соответствии с ней валютный курс представляет собой ни что иное, как предельный доход от внешнеторговых операций – импорта или экспорта.

Для случая осуществления экспортных операций валютный курс k(t) определяется следующим образом [5, с.1018]:

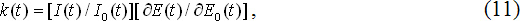
Содержательно соотношение (11) означает следующее: валютный курс (например, «рубль/доллар») показывает, сколько рублей надо дополнительно потратить, чтобы получить дополнительный доллар дохода.

Для случая осуществления импортных операций валютный курс k(t) определяется аналогичным образом [5, с.1018]:

В данном случае соотношение (12) предполагает следующую интерпретацию: валютный курс (например, рубль/доллар) показывает, сколько рублей можно дополнительно получить, если потратить дополнительный доллар на закупку импортного продукта.

Впоследствии С.Н.Журавлев встроил в эту систему еще и тарифные инструменты. В этом случае уравнения (11) и (12) уточняются следующим образом [6, с.580]:

Для оценки валютного курса по формулам (11)-(12) С.Н.Журавлев оценил коэффициенты регрессионного уравнения для экспорта E = α(E₀)^σ, где α и σ – параметры регрессии; для импорта им использовалась аналогичная модель [5, с.1018]. Вычисляя с помощью полученных эконометрических зависимостей соответствующие частные производные, он получил расчетные данные для валютного курса «рубль/доллар» на уровне 0,8–1,0 руб. за 1 долл. США. Как известно, именно такой курс и действовал в Советском Союзе. Таким образом, практические расчеты на стабильных статистических данных СССР подтвердили работоспособность концепции маржинальной эффективности внешнеторговых операций. Тем не менее, автором данных расчетов справедливо указывалось, что оцененный им курс плохо согласовался с интуитивными представлениями, согласно которым цена валюты должна быть по крайней мере на порядок выше, что подтверждалось валютным курсом «черного рынка» конца 80-х годов [4, с.633]. Данные неувязки базировались на огромных расхождениях в эффективности отдельных секторов экономики (потребительских продуктов и продукции производственно-технического назначения), что затрудняло «выведение» объективного обменного курса [4, с.634].

Нельзя не заметить и других недостатков изложенного метода. Хотя каждое из определений валютного курса (11) и (12) в целом можно признать экономически осмысленным и конструктивным, вызывает отторжение сама двойственность этого определения. Совершенно очевидно, что в ряде случаев оценки, получаемые на основе формул (11) и (12), будут неодинаковыми. В частности, С.Н.Журавлев и сам совершенно верно отмечал, что формулы (11)-(14) справедливы при условии внешнеторгового равновесия [6, с.580]. Но если это условие не выполняется (а на практике это бывает почти всегда), то как тогда рассчитать валютный курс?

В данном случае мы в очередной раз сталкиваемся с ограниченностью концепции равновесия. Для многих переходных и развивающихся экономик, а также экономик, находящихся в предкризисном или, наоборот, послекризисном состоянии, такой подход совершенно неприемлем. В этой связи можно констатировать, что в своем чистом виде концепция маржинальной эффективности внешнеторговых операций может применяться только для относительно благополучных экономических систем и, как правило, в долгосрочном аспекте.

2. Концепция удельной эффективности внешнеторговых операций. Данная концепция была предложена Л.А.Стрижковой в 1997 г. [7]. Центральным понятием данной концепции является удельная эффективность экспорта ƒ_E и импорта ƒ_M (все остальные обозначения прежние) [7, с.72]:

Подчеркнем, что в соотношениях (15)-(16) валютный курс используется как экзогенная (заданная) величина в отличие от формул (11)-(12), где он фигурирует в качестве эндогенной (определяемой) характеристики. Таким образом, рассматриваемая концепция изначально исходит из несовпадения удельных эффективностей экспорта ƒ_E и импорта ƒ_M. Но коль скоро валютный курс сам используется в расчетах в качестве исходной информации, то каков же закон его формирования в соответствии с рассматриваемой концепцией?

Пытаясь ответить на этот вопрос, Л.А.Стрижкова вводит понятие равновесного или «справедливого» валютного курса, при котором происходит выравнивание уровней доходности от операций с импортом и экспортом. Для этого соотношения (15)-(16) дополняются следующим условием равновесия:

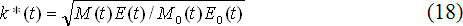
При разработке концепции удельной эффективности внешнеторговых операций изначально предполагалось, что она будет использоваться для анализа разбалансированной российской экономики переходного периода. В частности, расчеты по формулам (15), (16) и (18) показали, что в 1995 г. равновесный валютный курс «рубль/доллар» составлял 5,5 тыс. руб. за 1 доллар США против фактического курса в 4,6 тыс. руб. [7, с.72], т.е. российский рубль явно нуждался в девальвации. В 1996 г. эффективность импортных операций в 1,4 раза превышала аналогичную оценку для операций с экспортом [7, с.73], что по-прежнему предполагало девальвацию рубля.

В работе [4] Л.А.Стрижковой была дополнительно предложена модификация концепции удельной эффективности внешнеторговых операций, в которой вместо показателей (15)-(16) использовалось отношение прибыли к себестоимости. Фактически это означало замену предельно агрегированных макропоказателей (15)-(16) на микрохарактеристики, значительно более тонко учитывающие стимулы и мотивации экспортеров и импортеров. В частности, расчеты по данным показателям позволили выявить более яркую закономерность в российской экономике, чем на основе зависимостей (15)-(16): эффективность импорта в 1996 г. превышала эффективность экспорта примерно в 4 раза [7, с.71].

Последний факт говорит о том, что в России уже в 1996 году возникла объективная потребность в 2-кратной девальвации рубля. Эта потребность действительно была реализована, но в более широком масштабе и с запазданием на 2 года – в 1998 г. Таким образом, концепция удельной эффективности внешнеторговых операций имеет, если и не прогностическую ценность, то, по крайней мере, «объяснительное» значение при исследовании валютных курсов. Если же говорить о прикладных прогнозах, то данная концепция может претендовать в основном на формирование долгосрочных стратегических ориентиров в динамике обменного курса; учет краткосрочных эффектов данная методика не предполагает.

Однако следует отметить и некоторые специфические недостатки рассмотренной нами концепции. Во-первых, она ориентирована на определение так называемого равновесного валютного курса, а он, как правило, не совпадает с фактическим. В ряде случаев это несовпадение может быть очень существенным. Во-вторых, остается вопрос о том, какой вариант концепции следует применять: основанный на показателях (15)-(16) или на показателях рентабельности импортных и экспортных операций. Экономическая логика и практические расчеты говорят, что второй подход лучше, однако здесь имеется определенный «технический» нюанс. Остановимся на этом моменте чуть более подробно.

В работе [8] было показано, что при достаточно тщательной калькуляции показателя рентабельности для операций с импортом возникает «двойной эффект» со стороны валютного курса: он входит как в числитель, так и в знаменатель; для рентабельности экспортных операций такой ситуации не возникает. Если в этом случае воспользоваться условием равновесия (17), то получившееся искомое уравнение для отыскания равновесного валютного курса будет квадратным, которое предполагает значительно более сложную формулу расчета, чем соотношение (18). Кроме того, остается теоретическая возможность возникновения двух равновесных курсов, что еще больше осложняет прикладные расчеты.

Таким образом, для доведения рассмотренной выше концепции до уровня прикладного инструментария, по-видимому, должна быть усовершенствована сама методика расчетов показателей удельной эффективности импорта и экспорта. Использование же равновесного валютного курса в качестве ориентира для его фактической величины возможно только для более или менее сбалансированных экономик, чем ограничивается сфера применения концепции удельной эффективности внешнеторговых операций.

3. Неравновесные схемы концепции эффективности внешнеторговых операций. Данная концепция в настоящий момент до конца не оформилась, хотя и является логическим следствием предыдущих аналитических схем. В связи с этим дадим основные положения неравновесной концепции эффективности внешнеторговых операций в нашей собственной трактовке.

Если встать на позицию, в соответствии с которой, даже если равновесие отсутствует, то все равно в системе имеется тенденция к нему, то концепция удельной эффективности внешнеторговых операций позволяет записать следующее уравнение для динамики валютного курса (все обозначения прежние):

Модель (19) отражает тот факт, что изменения валютного курса определяются степенью несоответствия в эффективности импортных и экспортных операций; α – параметр, отражающий скорость адаптации валютного курса к неравновесию в эффективности внешнеторговых операций.

По-видимому, характер и направление основных движущих сил в формировании валютного курса модель (19) воспроизводит в целом правильно. Однако, как было отмечено выше, уже в 1996 г. с ее помощью можно было прогнозировать резкую (примерно 2-кратную) девальвацию. Однако этого не произошло, напряжение продолжало накапливаться на протяжении еще двух лет, после чего выразилось в катастрофическом обвале рубля. Сказанное свидетельствует, что наличие определенной инерционности наряду с резкими провалами в динамике валютного курса существенно ограничивают сферу практического использования неравновесной модели (19). Вместе с тем, она является хорошей теоретической основой для объяснения некоторых процессов, например, кризиса 1998 г.

Между тем и объяснительные возможности модели (19) ограничены. Так, например, она делает очевидной саму закономерность обвала рубля в 1998 г., но ничего не говорит о том, почему этот обвал произошел именно в 1998 г., а не в 1997 или в 1999 г. Следовательно, неравновесная схема эффективности внешнеторговых операций (19) в ряде случаев может успешно использоваться в долгосрочном прогнозировании; на коротких же временных отрезках она может только дезориентировать аналитика.

Применительно к теории предельной эффективности внешнеторговых операций обобщение на неравновесные случаи аналогично. Учитывая, что формулы (11) и (12) справедливы при равенстве предельных издержек экспорта и предельного дохода от импорта, фактический валютный курс должен изменяться в зависимости от расхождения между этими величинами:

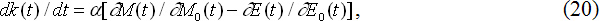
Все плюсы и минусы модели (20) точно такие же, как и модели (19). В этой связи встает еще одна проблема – какой концепции отдать предпочтение: удельной или предельной эффективности торговых операций? В настоящее время не хватает фактов, чтобы однозначно ответить на поставленный вопрос.

Представления о биржевом механизме формирования валютных курсов не являются новыми. Вместе с тем в своем законченном виде они «отшлифовались» относительно недавно. Наиболее простая и эффективная модель биржевых торгов применительно к курсу «рубль/доллар» была предложена в 1994 г. Ю.П.Лукашиным и А.С.Лушиным в работе [9]. Рассмотрим этот подход более подробно.

1. Общая схема биржевого механизма формирования валютных курсов. Теоретической и методологической основой построения модели биржевых торгов для валютного курса «рубль/доллар» являются два момента. Во-первых, в России фактический текущий валютный курс формируется на основе курса, устанавливаемого на очередных торгах Московской межбанковской валютной биржи (ММВБ). Во-вторых, сам процесс котировки иностранной валюты организован таким образом, что до начала торгов от коммерческих банков собираются заявки на покупку и продажу валюты. Данные заявки формируются коммерческими банками на основе валютного курса предыдущих торгов. Все это предполагает использование данной информации в качестве агрегатов спроса и предложения валюты. В-третьих, результатом проведения торгов является формирование такого валютного курса, при котором спрос на валюту и ее предложение уравновешиваются.

Схематично это означает, что переход в результате торгов от начального валютного курса k₀(t–1) к равновесному курсу k₁(t) = k₀(t–1) + Δk(t) приводит в равновесие изначально несбалансированный валютный рынок биржи, т.е. выполняется следующее уравнение [9, с.85]:

Помимо уравнения (21) модель валютных торгов включает зависимость спроса на валюту и предложения валюты от ее цены (валютного курса), которые в простейшем виде аппроксимируются следующими соотношениями [9, с.85]:

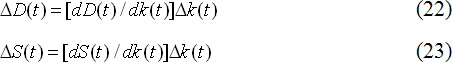
Тогда подстановка (22) и (23) в (21) дает искомую модель формирования валютного курса [9, с.85]:

где A(t) = 1/[dS(t) / dk(t) - dD(t) / dk(t)] – коэффициент пропорциональности, учитывающий степень гибкости спроса и предложения на изменения валютного курса.

Таким образом, модель (24) описывает реакцию валютного курса на несбалансированность биржевого валютного рынка. При этом через показатель A(t) в ней автоматически отражена обратная зависимость спроса и предложения от величины обменного курса.

Уже в таком общем виде, как уравнение (24), модель, предложенная Ю.П.Лукашиным и А.С.Лушиным, имеет важные особенности.

Во-первых, модель (24) является классической моделью рынка и в явном виде включает в свой состав такие величины, как спрос, предложение и цена. Фактически модель (24) есть ни что иное, как популярная модель ценообразования П.Самуэльсона. Разница лишь в содержании переменных: вместо цены в модели П.Самуэльсона в (24) фигурирует валютный курс, а вместо товарного спроса и предложения – денежно-валютный.

Во-вторых, модель (24), ориентированная на учет всех нюансов биржевого валютного рынка, носит краткосрочный характер. Среди моделей формирования валютного курса, рассмотренных нами выше, это первая модель такого рода. В этом заключается ее важное преимущество. Разумеется, оборотной стороной медали является то, что она совершенно не объясняет происхождение биржевых валютных потоков; она их берет в качестве экзогенных характеристик.

Безусловно, модель (24) следует воспринимать в качестве базовой конструкции. Различные модификации спроса и предложения от валютного курса будут автоматически сказываться на функциональной конфигурации коэффициента А(t).

2. Роль Центрального банка в формировании валютных курсов. Помимо возможности учета краткосрочных колебаний валютных курсов, неравновесная модель (24) имеет еще одно важное достоинство: в ней в явном виде может быть отражена регулирующая деятельность Центрального банка (ЦБ) страны. Для этого модель (24) переписывается в следующей форме [9, с.88]:

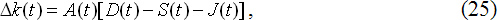
Исходя из того, что ЦБ может двояко вмешиваться в процесс валютных торгов, то и его интервенция J>0, если он продает валюту, и наоборот J<0, если ЦБ ее покупает. В первом случае (J>0) ЦБ увеличивает рыночное предложение валюты, а во втором (J<0) – он увеличивает рыночный спрос на нее.

Таким образом, Центральный банк страны, будучи самым мощным участником биржевого валютного рынка, оказывает непосредственное воздействие на рыночный валютный курс. Данный факт и отражает неравновесная модель (25).

Включение в теоретическую схему Центрального банка страны придает ей максимальную реалистичность и имеет большое объяснительное значение. В частности, именно в рамках этой модели можно элементарно объяснить произошедший обвал рубля в 1998 г.

Как известно, до августа 1998 г. действовал так называемый «валютный коридор», т.е. ЦБ России провозгласил, что как бы ни складывалась ситуация он своими валютными интервенциями удержит валютный курс в границах валютного коридора. Данный факт «выдавил» многих игроков с биржевого рынка, т.к. незначительные колебания валютного курса в рамках валютного коридора сильно ограничивали возможности получения спекулятивных прибылей. Однако систематические положительные интервенции ЦБ (J>0) предполагают наличие у него соответствующих валютных резервов. К середине 1998 г. данные резервы были исчерпаны и ЦБ объявил о «снятии» валютного коридора. Фактически в этот момент ЦБ России вышел из игры (J=0), а в условиях отсутствия централизованных интервенций биржевой спрос на валюту существенно превысил ее предложение, что и стимулировало катастрофический рост валютного курса. Ситуация усугубилась отказом Правительства РФ погашать свои долги. В этот момент практически весь спрос рынка ценных бумаг «перелился» на валютный рынок, стимулировав рост спроса на валюту.

Таким образом, именно модель (25) позволяет понять, почему и за счет чего валютный кризис 1998 г. произошел именно тогда, когда он произошел, а не раньше или позже. Кроме того, модель (25) предполагает два практических аспекта ее применения. Первый связан с прогнозированием валютного курса на основе имеющейся информации, второй – с расчетом величины необходимых интервенций для поддержания валютного курса на том или ином уровне. Подобный расчет выполняется элементарно, если выразить интервенцию через остальные переменные модели (25).

Разумеется, полное понимание возможностей Центрального банка страны для регулирования валютного курса предполагает еще учет динамики золотовалютных резервов ЦБ. Однако этот фактор связан с внешнеторговыми эффектами, которые в модели (25) никак не учитываются.

3. Асимметрия в биржевом процессе формирования валютных курсов. Возможности практического использования модели валютных торгов (25) ограничиваются еще рядом «технических» факторов. Рассмотрим некоторые из них.

Во-первых, процедура прогнозирования обменного курса требует «расщепления» базовой модели (25) на две субмодели: для растущего и падающего валютного курса. Это связано с тем, что на практике сам механизм формирования валютного курса существенно различается в зависимости от того, происходит его рост или снижение [9, с.88]. Более того, проведенные Ю.П.Лукашиным и А.С.Лушиным расчеты позволяют заключить, что механизм падения курса в целом хуже поддается количественному описанию, чем его рост [9, с.90]. Таким образом, можно говорить об определенной асимметрии процесса формирования курса с соответствующим прикладным результатом: в одну сторону его прогнозировать легче, в другую – труднее.

Во-вторых, сама природа биржевого валютного рынка такова, что отрицает тривиальные связи между спросом (предложением) и валютным курсом. Для построения соответствующих удовлетворительных эконометрических зависимостей приходится проводить определенную чистку ретроспективных рядов путем исключения из них некоторых точек, связанных, например, с паническим состоянием рынка [9, с.88]. Кроме того, выявленные зависимости оказываются весьма неустойчивыми и ненадежными; в любой момент может произойти перестройка механизма балансировки спроса и предложения.

Кроме того, эконометрические расчеты, проведенные С.В.Козловой в 1994 г. примерно за тот же период (1992-1993 гг.) на основе помесячной статистики, показали, что зависимости между валютным курсом «рубль/доллар» и валютными интервенциями ЦБ не наблюдается [10, с.76]. Это говорит о динамической ограниченности модели Лукашина-Лушина: агрегирование дневной биржевой статистики в ежемесячные данные приводит к «исчезновению» фактора валютных интервенций ЦБ. Между тем, на временном интервале с помесячной разбивкой на динамику курса начинают влиять совершенно другие, среднесрочные, факторы: неплатежи предприятий (с лагом в 1 месяц); централизованный кредит в целом и его составляющие [10, с.75].

Сказанное подводит к выводу, что модель (25), предложенная Ю.П.Лукашиным и А.С.Лушиным, относится к разряду «полутеоретических» моделей. Правильно отражая важные стороны в краткосрочном механизме формирования валютных курсов, она может быть применена и для практических расчетов. Однако это применение довольно ограничено и требует большой осторожности.

4. Учет динамики золотовалютных резервов Центрального банка страны. Как было указано выше, даже для приблизительной идентификации периода, когда биржевой валютный рынок может «обрушиться», как это было в России в августе 1998г., модель (25) необходимо дополнить уравнением динамики валютных резервов ЦБ. Так как в литературе подобного расширения модели (25) сделано не было, то ниже оно будет дано в авторской версии.

В самом упрощенном виде уравнение динамики золотовалютных резервов ЦБ можно записать следующим образом:

Модель (26) учитывает тот простой факт, что ЦБ, осуществляющий денежную эмиссию национальной валюты, фактически бесплатно для себя может покупать у юридических лиц ту часть выручки от экспорта, которая подлежит обязательной продаже. Разумеется, модель (26) очень грубо воспроизводит механизм формирования резервов. Так, в ней не учитывается доход ЦБ от игры на бирже и пополнение резервов за счет движения краткосрочных международных капиталов.

В соответствии с (26) валютные резервы ЦБ формируются за счет ежемесячных поступлений от экспорта и за счет серии биржевых валютных интервенций. Понятно, что при систематическом эффекте J>0 биржевые операции будут истощать резервы ЦБ страны, а при J<0 – они будут, наоборот, способствовать их накоплению. Вероятность возникновения девальвации национальной валюты начинает резко увеличиваться при приближении фактической величины валютных резервов ЦБ R(t) к своей минимально допустимой величине R_MIN, имеющей официальную регламентацию (R(t)→ R_MIN).

Таким образом, совместное использование моделей (25) и (26) позволяет осуществлять хотя бы ориентировочные прогнозы резкой девальвации национальной валюты.

Однако нельзя не отметить и ограниченности модели (25)-(26).

Во-первых, она ориентирована на весьма мощные тенденции в истощении валютных средств Центрального банка и не дает возможности прогнозировать незначительные сдвиги в стороны девальвации или ревальвации валюты.

Во-вторых, она имеет ярко выраженный «национальный» характер. Дело в том, что эта модель применима к экономике России, где сложился довольно простой биржевой механизм формирования валютного курса «рубль/доллар». Данный факт напрямую связан с тем, что российский рубль не является твердо конвертируемой валютой и зона его котировки вполне может ограничиваться площадкой ММВБ. Для твердо конвертируемых валют формируются мировые биржевые рынки, на которых механизм котировки национальных денежных единиц принципиально отличается от российского биржевого рынка.

1. Базовая версия концепции капитальных активов. Данная концепция разработана группой западных экономистов и к настоящему моменту является уже достаточно старой, можно сказать, классической. Ее основная идея заключается в том, что краткосрочная динамика валютного курса определяется текущими условиями на финансовых рынках [1, с.101]. Текущие же условия задаются процентными ставками. Тогда, согласно концепции капитальных активов, в силу высокой мобильности международных капиталов доход с денежных активов в любой валюте должен быть одинаковым. В этом случае обеспечивается валютное равновесие, общая схема которого может быть смоделирована в следующей форме.

Доход на имеющийся капитал в национальной валюте равен величине (1+r), где r – внутренняя номинальная процентная ставка (к примеру, процент по рублевым банковским вкладам). Однако владелец денежного актива может произвести альтернативную операцию: в начале рассматриваемого периода конвертировать свои средства в иностранную валюту по текущему валютному курсу k(t), «снять» с получившегося валютного актива процент (1+r₀), где r₀ – «зарубежная» номинальная процентная ставка (к примеру, процент по долларовым банковским вкладам), после чего произвести обратную конвертацию валютного актива в национальные денежные единицы по текущему валютному курсу следующего периода k(t+1). Тогда условие равновесия доходов с активов в национальных и иностранных денежных единицах запишется следующим образом [2, с.60]:

Данное уравнение можно преобразовать к виду (все обозначения прежние):

Таким образом, валютный курс определяется разрывом в соответствующих процентных ставках. Модель (28) является квинтэссенцией концепции капитальных активов (для большей наглядности и простоты знаменатель в (28) часто опускается, а числитель называется дифференциалом процентных ставок).

Ранние попытки эконометрической проверки данной концепции не дали четкого результата. В частности, исследование Л.Оксельхейма динамики курса шведской кроны по отношению к валютам США, Японии, ФРГ и Великобритании за 1974-1984 гг. на основе ежемесячной статистики показало существенные расхождения между динамикой курсов и процентных ставок, в качестве которых использовались ставки по трехмесячным государственным облигациям. Причем с 1978 по 1984 г. данные расхождения возросли, что говорит о «вклинивании» в процесс каких-то иных факторов, определяющих валютные курсы [1, с.124]. Таким образом, говорить о безусловной выполнимости условия (28) нельзя.

Более поздние расчеты, выполненные А.Ивантером и А.Пересецким на основе ежедневных данных о российских финансовых рынках за период с 5 мая по 31 июля 1997 г., показали определенную, хотя и очень небольшую, связь между текущим валютным курсом и доходностью государственных краткосрочных обязательств (ГКО) [11, с.33]. Следовательно, даже если модель (28) и не выполняется в чистом виде, то, по крайней мере, ее частные модификации могут быть вполне работоспособны.

Следует особо отметить следующий момент. Модель (28) оперирует процентными ставками. Однако в общем случае не ясно, что именно брать в качестве соответствующих индикаторов. Иногда в расчетах фигурируют проценты по государственным облигациям, иногда – ставки по банковским вкладам.

Однако в любом случае, похоже, что при всей своей ограниченности концепция капитальных активов имеет большее значение, чем это признается экономической теорией. Примером тому может служить ситуация с евро. Фактически вся недолгая история новой валюты представляет собой довольно жесткую схватку с долларом. После начального корректирующего понижения курса «доллар/евро» началась, порой, неоднозначная, но довольно верная тенденция его дальнейшего снижения. Дорогой доллар невыгоден европейским странам, в больших объемах импортирующих энергоносители и сырье. Дорогой импорт сказывается на их внутренних ценах и инициирует инфляционные тенденции. Данный факт и предопределил длящуюся уже около года так называемую «войну процентных ставок» [12, с.4]. Пытаясь изменить нежелательную курсовую тенденцию, Европейский центральный банк в середине 2000 г. осуществил беспрецедентную акцию – повысил процентную ставку по вкладам в евро сразу на 0,5%. Результат увеличения дифференциала процентных ставок не замедлил сказаться: котировка евро на мировых биржах пошла вверх. В целом же понижательная тенденция курса «доллар/евро» довольно хорошо согласуется с концепцией капитальных активов, т.к. до сих пор разрыв между ставкой по вкладам в евро (4,25% на середину 2000 г.) и в долларах (6,25%) составляет примерно 2% в пользу доллара [12, с.4].

Сказанное позволяет констатировать, что фактор процентных ставок не может не учитываться при формировании динамики валютных курсов. Возможно, связь между курсом и дифференциалом процентных ставок не столь проста, как это постулируется моделью (28), но и отрицать ее было бы неверно. Однако пока, на наш взгляд, остается открытым следующий вопрос: какова длина временного интервала, на котором применение концепции капитальных активов является эффективным?

2. Экспектационная версия концепции капитальных активов. Данная концепция представляет собой довольно простое обобщение модели (27). Для этого в приведенной выше базовой схеме (27) меняется только один элемент: обратная конвертация валютного актива в национальные денежные единицы происходит не по текущему валютному курсу следующего периода k(t+1), а в соответствии с неким ожидаемым в момент t значением k_E(t+1). Тогда условие равновесия (27) перепишется следующим образом:

В соответствии с моделью (29) текущий валютный курс формируется под непосредственным воздействием со стороны ожиданий (экспектаций) его будущих значений. В ряде случаев при конкретизации модели (29) в качестве фактического валютного курса фигурирует спот-курс k_S(t), а в качестве ожидаемого – форвардный курс k_F(t+1) [2, с.60]:

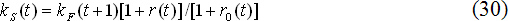
Основным недостатком обеих версий концепции капитальных активов является их равновесный характер. На самом деле полного выравнивания прибыльности различных активов никогда не происходит. Система просто колеблется между состояниями относительной выгодности и невыгодности той или иной валюты. И в ряде случаев валютный рынок может довольно далеко «убегать» от своего равновесного состояния.

1. Модели сосредоточенных экспектаций. Фактор ожиданий уже заложен в экспектационной версии концепции капитальных активов. Однако дальнейшее изучение этого фактора привело к оформлению теории экспектаций в самостоятельное направление экономического анализа. При построении прикладных моделей валютных курсов используется два кита указанной теории: гипотеза о рациональности ожиданий экономических агентов и гипотеза об эффективности валютного рынка. Применительно к исследованию динамики валютных курсов гипотеза о рациональности ожиданий означает, что фактический спот-курс совпадает со своим ожидаемым значением (т.е. ожидания настолько хороши, что попадают прямо в точку). Формально это можно записать следующим образом:

Гипотеза об эффективности валютного рынка означает, что форвардный курс «вбирает» в себя всю доступную информацию об ожиданиях экономических агентов в отношении будущего валютного курса. Формально это можно отразить следующим образом:

Комбинация соотношений (31) и (32) позволяет построить простейшую эконометрическую модель:

Так как вся позитивная информация, определяющая текущий валютный курс, сосредоточена в форвардном курсе за предыдущий период, то и модель (33) можно квалифицировать как модель сосредоточенных экспектаций.

Расчеты по модели (33), выполненный Я.Френкелом для курсов американского доллара по отношению к английскому фунту, французскому франку и немецкой марке на основе ежемесячной статистики с июня 1973 по июнь 1979 г., дали позитивный результат [1, с.106]. Эмпирическое исследование Ф.Абрахама, проведенное для курса бельгийского франка по отношению к марке ФРГ и доллару США на основе ежемесячных данных с 1978 по 1983 г., также подтвердило выполнимость уравнения (33) [1, с.107]. Более поздние расчеты, проведенные М.В.Ершовым для курса «марка/доллар» на основе квартальных данных с 4-го квартала 1975 по 2-ой квартал 1987 г., еще раз продемонстрировали справедливость модели (33) [2, с.56].

Особо стоит отметить более «свежие» расчеты, выполненные А.Ивантером и А.Пересецким на основе ежедневных данных о российских валютных рынках за период с 5 мая по 31 июля 1997 г., которые показали довольно высокую связь между форвардным и текущим курсами (коэффициент корреляции составил 0,9) [11, с.33]. Следовательно, даже для «молодого» финансового рынка России теория валютных ожиданий дает неплохие эмпирические результаты.

Таким образом, модель валютных экспектаций (33) вполне пригодна для учета краткосрочных эффектов в динамике валютных курсов. Однако справедливости ради следует отметить, что имеются исследования, отрицающие в определенных случаях работоспособность модели (33) [1, с.108].

2. Модели распределенных экспектаций. Итак, хотя модель (33) довольно хорошо зарекомендовала себя, она все же не является универсальной. Поэтому иногда приходится переходить к модифицированным моделям валютных экспектаций. Простейшим примером такой модификации может служить регрессия вида [1, с.107]:

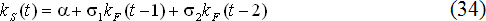
В соответствии с моделью (34) эффект, идущий со стороны форвардного рынка, распределен между двумя значениями форвардного курса, в связи с чем и сама модель отображает распределенные экспектации. Переход к такой модели связан с отбрасыванием гипотезы об эффективности валютного рынка. Теоретически данный факт является, конечно, достаточно неприятным, однако общая идея зависимости спот-курса от форвардного рынка сохраняется. Все остальные плюсы и минусы модели такие же, как для модели (33).

1. Концепция торгового баланса. В соответствии с кейнсианской моделью открытой экономики одним из факторов, влияющих на валютный курс, является торговый баланс страны [1, с.100]. Действительно, именно торговый баланс является первичным фактором формирования спроса и предложения на валютном рынке страны. Простейшей базовой моделью, которая может использоваться для описания движения валютного курса, такова (все обозначения прежние):

Данная модель по сути дела представляет собой макроэкономическую версию модели ценообразования П.Самуэльсона применительно к иностранной валюте.

В некоторых случаях более удобными считаются модификации модели (35), учитывающие внешнеторговые агрегаты не в абсолютной, а в относительной форме. К числу таких моделей относится, например, регрессионная модель Ю.В.Ермолаевой [13, с.49]:

Прикладные расчеты, проведенные Ю.В.Ермолаевой с помощью (36) на основе ежеквартальной статистики за период с 1 квартала 1995 г. по 1 квартал 2001 г., показали ее принципиальную пригодность, хотя точность аппроксимации оставляет желать лучшего [13, с.52]. Для повышения точности модельных расчетов модель может быть подвергнута дополнительной калибровке. В частности, вместо уравнения (36) можно использовать его рекурсивный аналог [13, с.56]:

Подобное использование «темповой» разновидности схемы торгового баланса позволяет существенно улучшить статистические характеристики эконометрической модели.

Таким образом, прикладные расчеты показывают, что, несмотря на свою явную упрощенность, концепция торгового баланса дает вполне приемлемые результаты.

Вместе с тем известно множество случаев, когда модели (35) и (36) не срабатывают. Как справедливо подметил Дж.Сорос, дефицит торгового баланса США составляет примерно 3% ВНП и имеет тенденцию к росту, в то время как 11 стран-членов зоны евро и Япония имеют положительное сальдо внешней торговли [14, с.372]. Казалось бы, что такая ситуация должна естественным образом привести к укреплению евро и йены по отношению к доллару, но на практике обе валюты постепенно девальвируются. Таким образом, даже при анализе таких фундаментальных соотношений сил в мировой экономике модели (35) и (36) способны дезориентировать исследователя.

Ограниченность объяснительных и предсказательных возможностей моделей (35) и (36) частично может быть объяснена тем, что в ней, как правило, импорт и экспорт учитывается в долларовом выражении [13, с.56]. Между тем масса импортных и экспортных операций проходит в совершенно другой валюте. Таким образом, данная схема даже для курса «рубль/доллар» подходит не идеально, а для курсов других валют (например, «рубль/евро») вообще сомнительна. Для адаптации схемы торгового баланса импорт и экспорт следует учитывать только в части объемов, проведенных в соответствующей валюте. Однако на практике такой статистический учет проблематичен.

2. Концепция платежного баланса. Ограниченность схемы (35)-(36) легко снимается путем ее обобщения на платежный баланс. Для этого модель (35) можно переписать в следующем виде:

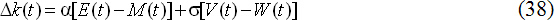
Необходимость перехода к расширенной схеме (38) хорошо выражена словами Дж.Сороса, характеризующего состояние в странах Юго-Восточной Азии накануне финансового кризиса 1997 г.: «диспропорции между состоянием торговых балансов и счетов операций с капиталом превысили разумные пределы» [14, с.279]. Иными словами, на практике следует учитывать двойное напряжение: в сфере внешней торговли и в сфере движения капиталов.

Осознавая тот факт, что экспорт и импорт товаров и услуг представляют собой довольно «грубые» статистические агрегаты, некоторые аналитики вводят в модельный анализ дополнительные факторы из платежного баланса. В частности, Ю.В.Ермолаевой была использована следующая модификация модели (2) [13, с.53]:

Однако опыт показал, что подобное уточнение модели (36) мало, что дало для повышения точности эмпирических расчетов [13].

Надо сказать, что наряду с указанной выше имели место и другие попытки более полного учета структуры платежного баланса при формировании величины валютного курса. В частности, модель (36) преобразовывалась в следующее соотношение [13, с.47]:

Однако точность расчетов по столь детализированной модели оказалась низкой [13, с.48] и, следовательно, скрупулезный учет ключевых агрегатов платежного баланса себя в целом не оправдал. Кстати говоря, корреляционный анализ показал, что связь между валютным курсом и изменениями валютных резервов оказалась крайне слабой [13, с.46].

Таким образом, практическое применение концепции платежного баланса для анализа и прогнозирования валютных курсов требует более тонких модельных схем; «лобовая атака» здесь, как правило, не приносит хороших результатов.

Представленный выше обзор моделей, теорий и концепций формирования валютных курсов являет собой довольно эклектичное методическое месиво. Как же быть с имеющимся модельным плюрализмом?

Попытка отбросить все «плохие» схемы, оставив только самую «хорошую», обречена на провал. Дело в том, что все они доказали на практике свою работоспособность в определенных ситуациях и, следовательно, ни от одной из них нельзя отмахнуться просто так. Вместе с тем, ни одна из них не является настолько универсальной, чтобы заменить собой все остальные. Как же тогда быть?

Первое, что приходит на ум, это интегрировать все рассмотренные схемы в рамках одной глобальной многофакторной модели. Почему бы, например, не построить эконометрическую модель, в которой в качестве факторов фигурировали бы паритет покупательной силы (или его отклонение от текущего валютного курса), дифференциал процентных ставок, торговый (платежный) баланс и т.д.?

К сожалению, это невозможно. Дело в том, что все представленные выше модели различаются, если так можно выразиться, по степени срочности. Одни рассчитаны на работу с дневной статистикой, которая не имеет квартальных или годовых аналогов (например, валютные интервенции ЦБ). Другие рассчитаны на работу с усредненными годовыми данными, детализация которых до дневных значений будет просто абсурдной (например, значения паритета покупательной силы и торгового баланса). Таким образом, нельзя «загнать» в одну модельную конструкцию принципиально несоизмеримые экономические показатели.

С другой стороны модельный плюрализм является объективным отражением ограниченности математического инструментария при описании экономических явлений. Коснемся этого вопроса с философской точки зрения.

Дело в том, что сама ограниченность математики в экономике связана с глубоким антагонизмом между математической и диалектической логикой. Математическая логика направлена на описание неких непротиворечивых целостностей. Жизнь же диалектична и протекает в соответствии с законами диалектической логики. В соответствии с последними все социальные целостности постоянно развиваются, доходя на определенном этапе до так называемого отрицания отрицания. Фактически речь идет об изменении самой целостности. Однако математика не может работать с «распадающейся» целостностью. Отрицание отрицания, естественное для социальных миров, представляет собой логическое противоречие для математики. Именно поэтому все экономические законы временны, а модели имеют ограниченную область применения. Качественно новые витки в развитии социальных систем не могут быть описаны в рамках одной математической модели. Здесь уместна аналогия с принципом несводимости различных форм материи друг к другу. Нельзя описать биологические процессы в рамках химических формул, так же как нельзя свести социальные процессы к биологическим.

Имеющийся плюрализм моделей формирования валютных курсов, на наш взгляд, имеет и еще одну, математическую, аналогию. Если мы попытаемся аппроксимировать сильно нелинейную кривую прямой линией на всей области ее определения, то получим чудовищную погрешность. Однако каждый отдельный маленький участок этой кривой можно довольно успешно аппроксимировать маленькими прямыми отрезками. То есть, чем более дробной мы представим исходную кривую и чем больше будет аппроксимирующих линейных отрезков, тем выше будет точность аппроксимации. На этом принципе базируется известный принцип математики о том, что все процессы линейны в малом. Тоже самое наблюдается при возникновении модельного плюрализма: на каждом отдельном временном отрезке действуют свои экономические законы и факторы формирования валютных курсов. При переходе к более длинным временным отрезкам сама социальная целостность преобразуется, в ней происходит отрицание отрицания. Этим и обусловлен переход к другой экономико-математической модели. В каком-то смысле, чем больше таких моделей, работающих для соответствующих интервалов времени, тем точнее будет каждая из них на своем участке и тем эффективней будет весь модельный комплекс.

Вышеприведенные умозрительные рассуждения легко конкретизируются для рассмотренной нами системы моделей формирования валютных курсов. Так, при объяснении и прогнозировании дневных колебаний курса решающее значение играет биржевой рынок. Спрос на валюту и ее предложение вкупе с вмешательством со стороны ЦБ в виде его валютных интервенций полностью определяют текущий курс. В свою очередь текущая ситуация формирует ожидания экономических агентов, а ожидания в значительной степени поддерживают текущий валютный курс. Поэтому на «короткой дистанции» себя довольно хорошо проявляют модели биржевых торгов и модели валютных экспектаций.

Если же рассмотрение процесса простирается на месяц и более, то законы биржевой торговли утрачивают свое значение и начинают «вклиниваться» другие факторы, которые уже формируют не дневные флуктуации курса, а способны придать его динамике то или иное направление, тренд. Власть форвардного рынка над будущей динамикой цены валюты не распространяется слишком далеко и в районе квартала начинает заметно убывать. В это же самое время начинают «встревать» в процесс такие инструменты как процентные ставки. На уровне квартальных отрезков времени подключаются еще и валютные потоки, формирующиеся в результате экспорта и импорта товаров и услуг. На годовых отрезках «включается» фактор эффективности экспорт- и импорториентированных секторов, а еще на более длинных временных интервалах начинает работать сила «притяжения» паритета покупательной силы.

Из сказанного ясно, что законы одного временного деления нельзя экстраполировать на другие, более длинные (или короткие), деления. Нельзя и просто «слепить» воедино все модели.

Но коль скоро нельзя построить всеобъемлющую интегральную модель, то как же все-таки быть?

На наш взгляд, в данной ситуации можно сделать только одно – придумать некий алгоритм эффективного манипулирования всеми концепциями и моделями. Иными словами, модельный плюрализм должен сохраняться, но с помощью предполагаемого алгоритма он примет упорядоченный характер, что снимет остроту существующего теоретического антагонизма.

Можно ли в настоящий момент предложить такой алгоритм? По-видимому, нет. В общих чертах этот алгоритм ясен: при агрегировании отрезков времени должен осуществляться последовательный переход от одной модели к другой. Однако сказать что-либо конкретное о длине этих отрезков и последовательности «модельных сдвигов» трудно. Для этого должны быть проведены специальные исследования, изначальной целью которых будет выявление периодов устойчивости для каждой модели.

Конкретизируем сказанное. Допустим, что расчеты показали следующее: информационное обеспечение модели валютных торгов требует ретроспективной ежедневной информации с «глубиной» в полтора месяца. При этом выявлено, что построенная на основе такой информации модель сохраняет свою силу в течении полумесяца, после чего ошибка прогноза начинает резко нарастать. Следовательно, данная модель может использоваться для прогнозов в рамках двух недель. Для получения более «длинных» прогнозов следует переходить к другой модели и т.д.

Следует иметь в виду, что даже если и удастся сформировать искомый модельный комплекс, то его эффективность будет зависеть от целей его использования. Скорее всего, ни одна модель не позволит проводить прогнозы в утилитарных коммерческих (спекулятивных) целях. Кроме того, работа на основе данного модельного комплекса никогда не сможет быть полностью автоматизирована; оперативное вмешательство здравого смысла может потребоваться в любой момент.

Большое значение на формирование самого набора моделей и, разумеется, алгоритма работы с ними оказывает тот факт, насколько рассматриваемая экономика является неравновесной. Важным моментом проведенного выше обзора является уяснение того, что в такой стране, как Россия деформации между основополагающими экономическими параметрами могут быть столь вопиющими, что ни о каких равновесных концепциях формирования валютного курса не может быть и речи. В этом случае следует переходить к построению индикаторов, фиксирующих отклонение фактического курса от его равновесного значения. Диагностика подобных показателей позволит отслеживать накапливающееся в экономической системе напряжение и тем самым понять направление будущей динамики курса и определить вероятность наступления «обвалов» типа девальвации рубля 1998 г.

1. Филаточев И.В. Концепции «открытой экономики»: Интернационализация и макроэкономическая политика государства. М.: Наука. 1991.
2. Ершов М.В. Валютно-финансовые механизмы в современном мире (кризисный опыт конца 90-х). М.: Экономика. 2000.
3. Первозванский А.А. О соотношении между темпом инфляции и обменным курсом// «Экономика и математические методы», №4, 1998.
4. Журавлев С.Н. О проблемах перехода к открытой экономике// «Экономика и математические методы», №4, 1990.
5. Журавлев С.Н. Иностранные инвестиции в экономику: возможности регулирования объемов и структуры// «Экономика и математические методы», №6, 1990.
6. Журавлев С.Н. Рецессия в экономике экс-СССР: общие закономерности и специфические черты// «Экономика и математические методы», №4, 1992.
7. Стрижкова Л.А. Роль макроэкономических исследований в государственном управлении экономикой переходного периода. М. ИМЭИ. 1997.
8. Балацкий Е.В. Эффективность внешнеторговых операций: тарифы и валютное равновесие// «Мировая экономика и международные отношения», №6, 1998.
9. Лукашин Ю.П., Лушин А.С. Статистическое моделирование торгов на Московской межбанковской валютной бирже// «Экономика и математические методы», №3, 1994.
10. Козлова С.В. Анализ факторов, влияющих на валютный курс рубля// «Экономика и математические методы», №3, 1994.
11. Ivanter A., Peresetsky A. The development of the state bond market// «Working paper series», №99/06, May 1999.
12. Катин В. Война процентных ставок// «Независимая газета», 16.06.2000.
13. Стрижкова Л.А., Ермолаева Ю.В., Гончаренко А.Н., Журавский В.П. Моделирование взаимосвязей платежного баланса с макроэкономическими показателями прогноза. Научный доклад. М.: ИМЭИ. Сентябрь 2001.
14. Сорос Дж. Открытое общество. Реформируя глобальный капитализм. М.: Некоммерческий фонд «Поддержки Культуры, Образования и Новых Информационных Технологий». 2001.