Модель региональной экономики в ситуации мирового кризиса

1. Новые вызовы технологии моделирования. Математическое моделирование – важный общепринятый инструмент социально-экономических исследований и прогнозов. Однако использование традиционных форм этого инструмента в условиях современного мирового кризиса существенным образом затруднено. Особенно сильно кризис ухудшил точность статистических прогнозов экономики, и это вполне понятно, поскольку статистические расчеты предполагают достаточное постоянство тенденций, а кризис проявляется как их нарушение.

Предлагаемая нами технология моделирования позволяет смягчить возникшие затруднения. В ситуации, осложненной мировым кризисом, эта технология позволяет решать такие задачи как:

Представляемую разработку отличает от ранее выполненных авторами работ принцип существенной избыточности расчетных условий, обеспечивающий компьютерное согласование неограниченного количества экспертных, статистических и теоретических оценок и зависимостей, определяющих как отдельные моделируемые показатели, так и связи между ними.

Для проверки адекватности предлагаемой технологии на примере данных ряда российских регионов проведено сопоставление модельных оценок для показателей 2004-2008 годов и 1-2 кварталов 2009 г с фактическими данными. Полученные по большинству показателей результаты являются вполне удовлетворительными.

2. Исходные требования к технологии моделирования. Отправным пунктом предлагаемой разработки являются три факта.

Во-первых, очевидная трудность «кризисного» моделирования состоит в опасности накопления больших ошибок, обусловленных тем, что в кризисной ситуации существенно снижается точность всех информационных составляющих социально-экономического моделей – экспертных оценок, статистических расчетов и теоретических зависимостей. Если в стабильной экономической ситуации экспертные и статистические годовые прогнозы объемов производства нередко имеют погрешность до 1%, то в условиях кризиса аналогичные оценки вполне могут давать ошибку в 5-10 и более процентов. При обычном подходе к моделированию, где ошибки используемых оценок накапливаются, погрешность исходных оценок в 1% выглядит приемлемой и дает ошибку 3-6% в результирующих оценках, но ошибка в 10% в исходных оценках полостью обесценивает прогноз.

Во-вторых, полезные сведения, заключенные в используемых информационных составляющих моделей (в частности, в экспертных оценках), при обычном подходе к моделированию задействуются не полностью; например, теряется «неудобная» информация, которая плохо увязывается с остальными учитываемыми моделью факторами.

В-третьих, неточно известные величины при обычном математическом моделировании либо заменяются точными по форме оценками, либо рассматриваются как случайные, характеризуемые определенным законом распределения, описанным тем или иным способом (например, математическим ожиданием и среднеквадратичным отклонением). Замена неточно известных величин точными оценками порождает большую неконтролируемую погрешность, а использование законов распределения неудобно и не вполне корректно, поскольку неточность и случайность – понятия отнюдь не тождественные.

Эти факты определили ключевые требования к предлагаемой технологии моделирования:

3. Методические принципы расчетов. Предлагаемая разработка опирается на классическое представление о неполной определенности (недоопределенности) поведения экономических систем [1–2]. Недоопределенное поведение находится в очевидном противоречии с обычной практикой математического моделирования экономики, где недоопределенность либо просто игнорируется как несущественный фактор, либо подменяется случайностью. Пренебрежение фактором недоопределенности или сведение этого фактора к случайности принципиально неадекватно любой экономической ситуации. В условиях кризиса эта неадекватность особенно важна.

В основе разработки лежат три методических принципа:

Недоопределенность показателей позволяет адекватно отразить в модели недоопределенность поведения экономических систем. С этой целью мы рассматриваем большинство моделируемых показателей как недоопределенные величины, область значений которых достаточно хорошо известна, но точные значения не вполне определены. Если обычная величина есть число, то недоопределенная – это числовой интервал (от… до…). По мере поступления дополнительной информации недоопределенность сужается и в пределе недоопределенная величина может стать точной.

Математические действия достаточно легко обобщаются на случай недоопределенных величин. Пусть, например, недоопределенные величины А и В есть интервалы А=[1,2] и В =[0,1]. Тогда А+В =[1,3], А-В=[0,2] и т.д.

Простейшая недоопределенная величина – это недоопределенная константа (Н-константа).

Обобщение математических действий на случай недоопределенных величин позволяет ввести и понятие недоопределенной функции. Например, линейная зависимость y=а+b*x при недоопределенности одной или обеих ее констант (параметров) а и b есть недоопределенная функция (Н-функция). Статистические уравнения регрессии, широко используемые в экономическом прогнозировании, во многих случаях удобно рассматривать именно как недоопределенные отношения.

Принцип представления зависимости показателей как ограничений касается и экспертных оценок, и результатов статистических расчетов, и теоретических зависимостей. В соответствии с этим принципом любая учитываемая взаимосвязь рассматривается как ограничение области возможных состояний экономики. При наличии нескольких ограничений область решений задачи есть пересечение подмножеств, отвечающих каждому из ограничений.

Отдельные ограничения могут быть очень грубыми, но когда их много, то их совместное рассмотрение позволяет получить достаточно точные результирующие оценки. Например, имеем три разные оценки годового роста потребительских цен: от 0 до 13%, от 3 до 18%, от 11 до 40%. Каждая из оценок выглядит слишком грубой. Но результирующая оценка, совместимая со всеми тремя, составляет от 11 до 13%, т.е. имеет вполне приемлемую для практических целей точность.

Представление зависимости показателей в виде ограничений хорошо согласуется с принципом недоопределенности. Например, система неравенств, вырезающая из области возможных значений величины С подобласть С>=2 и С=<3, позволяет рассматривать С как недоопределенную величину, значения которой есть интервал [2, 3].

По содержательному смыслу рассматриваемые ограничения подразделимы на две группы: исходные оценки показателей и связи показателей. Они позволяют выразить всю основную информацию, используемую при моделировании.

Ценным свойством возникающих систем ограничений является их способность без дополнительной внешней информации корректно уточнять недоопределенные величины. Пусть, например, задана система ограничений, включающая

Легко видеть, что эта система приводит к уточнению интервалов А и В: А =[7,8], В =[2,3], причем это уточнение не требует никакой информации помимо самих ограничений.

Понятно, что рост числа учитываемых ограничений позволяет дополнительно уточнить результат. Но увеличение количества ограничений при неизменном числе рассматриваемых показателей способно привести к появлению совокупности ограничений неразрешимых, несовместных. Например, может возникнуть система независимых друг от друга линейных уравнений с числом уравнений, превосходящим число неизвестных.

В такой ситуации кажется естественным исключить «лишние» уравнения из модели. Но какие уравнения следует исключить? Каков экономический смысл исключаемых уравнений? Действительно ли они не несут полезной информации? Вполне возможна ситуация, когда кажущаяся несовместность некоторых ограничений отражает их приближенный характер. В этом случае исключение «лишних» уравнений приведет к потере полезной, а, возможно, и важной информации. Чтобы эту информацию не потерять, надо устранить несовместность не путем отбрасывания «лишних» уравнений, а путем учета приближенного характера используемых ограничений. Например, два условия С=4.2 и С=4.4 формально противоречат друг другу, но если считать эти условия приближенными и имеющими ошибку 5%, то они означают оценки С=[3.99,4.41] и С=[4.18,4.62] соответственно. Учитываемые вместе, эти оценки дают результат С=[4.18,4.41], т.е. описывают Х точнее, чем взятые порознь.

Принцип избыточности расчетных условий предполагает использование максимально полных систем ограничений, учитывающих всю доступную информацию, относящуюся к рассматриваемой задаче. Такие системы формально выглядят избыточными и несовместными, но становятся совместимыми, если учитывать приближенный (недоопределенный) характер ограничений. Например, три нетождественных выражениях одной и той же зависимости формально противоречат друг другу, но при учете их погрешности, взятых вместе, дают более точное представление об описываемой ими зависимости, чем взятые порознь.

Разумеется, все учитываемые ограничения (в том числе – избыточные) должны быть разумными и обоснованными. Ложные или выпадающие из общего ряда оценок ограничения приходится отбрасывать подобно тому, как при обработке статистики отбрасывают данные ложные или слишком выпадающие из общего ряда.

Избыточность расчетных условий позволяет более полно учитывать используемую информацию, делает решение более устойчивым и противодействует накоплению ошибок. Например, при расчете расходов бюджета в дополнение к условиям, ограничивающим слагаемые расходов, полезно ввести формально избыточное условие, ограничивающее всю сумму расходов и мешающее накоплению ошибок в оценке этой суммы. Также полезно ввести промежуточные ограничения на суммы некоторых статей расходов. Иначе говоря, вместо накопления ошибок отдельных расчетных зависимостей, характерного для обычного подхода к моделированию, в предлагаемом подходе реализуется взаимопоглощение ошибок.

Легко заметить, что в рамках предлагаемого подхода обычное деление показателей моделирования на входные и выходные заменяется делением значений показателей на исходные и результирующие. Исходные оценки могут быть заданы для всех показателей модели и в этом смысле все показатели могут выглядеть как входные. Но в результате учета связей показателей их недоопределенные значения способны уточниться. Эти новые (уточненные) оценки являются результирующими (выходными) и также могут относиться ко всем или большей части параметров.

4. Расчетные показатели и зависимости. Пример перечня моделируемых показателей региона, а также содержательный смысл и особенности применения используемых при этом зависимостей, дает табл.1.

Отметим, что при работе модели все расчетные условия выступают как единая система уравнений. При этом изменение любого из показателей влечет за собой соответствующие изменения (уточнения) других параметров. Например, изменения бюджетных показателей влияют на оценки объемов производства через посредство налогов, оттоков и бюджетных инвестиций.

5. Аппарат расчетов. В общем виде рассматриваемая задача моделирования описывается следующим образом. Имеется список показателей x₁, x₂ ..., xn с исходными оценками (областями значений) X₁, X₂, ..., X_n , a также множество зависимостей r_i(x₁,x₂,...,x_n)=0, i=1,...,k, выражающих связи показателей. Требуется найти все наборы значений < a₁, a₂,...,a_n > (a_ieX_i), показателей x₁, x₂ ..., x_n, которые отвечают всем зависимостям r_i.

При внешней простоте формулировки такая задача несет в себе большую вычислительную сложность и обычно не решается средствами традиционной математики. Укажем лишь самые очевидные причины сложностей:

Невозможность решения задачи традиционными методами заставляет обратиться к методам нетрадиционным. В качестве такого метода нами использована технология недоопределенных вычислений и недоопределенных моделей [3–6], специально созданная для расчетов с использованием недоопределенных величин и относящаяся к области constraint programming. Отметим, что constraint programming с конца ХХ века активно развивается в мире в качестве одного из наиболее перспективных направлений прикладной математики, а недоопределенные модели (Н-модели) значительно повышают точность, достоверность и обоснованность расчетов в условиях неполной, недоопределенной, неточной и противоречивой информации [7–11].

6. Работа с моделью. Возможность директивного задания любых моделируемых показателей – крайне ценное свойство предлагаемой технологии. Например, если задан размер ВРП, который надо достичь в 2010 году, то модель путем согласования показателей автоматически определяет те значения показателей 2009 и 2010 гг., которые необходимы для достижения заданной величины ВРП. Если же в рамках расчетных условий желаемая величина ВРП недостижима, то модель уведомляет об этом пользователя. Весьма полезной для практики экономических исследований представляется возможность директивного задания цен, объемов производства, инвестиций.

Модель обеспечивает автоматическое сжатие интервальных оценок показателей при поступлении дополнительной информации: при вводе в модель новых статистических данных расчетные показатели автоматически уточняются, а соответствующие прогнозные интервалы сужаются. Способность модели к автоматическому уточнению при поступлении новых данных позволяет в течение длительного времени использовать однажды созданную модель, постепенно дополняя ее поступающей информацией.

В процессе работы с моделью не требуется с самого начала определять и водить в модель все необходимые для расчета условия. Целесообразность ввода многих расчетных условий может определяться по ходу моделирования.

Получив некоторый модельный расчетный результат, пользователь имеет возможность его оценить и ввести в расчет дополнительные условия, задав уточненные значения некоторых показателей либо зависимостей. Новый результат будет служить ориентиром, определяющим целесообразность других уточнений и этот процесс можно повторять многократно.

Уведомляя пользователя о задании невыполнимых условий, модель страхует его от возможных ошибок. Выполнимые условия, уточняя систему расчетных оценок, сужают интервалы недоопределенности показателей (как задаваемых пользователем, так и связанных с ними). В итоге можно получать весьма узкие интервалы прогнозных показателей.

В качестве примера рис.1–3 демонстрируют результаты расчета и пошагового уточнения ряда экономических показателей одного из регионов России:

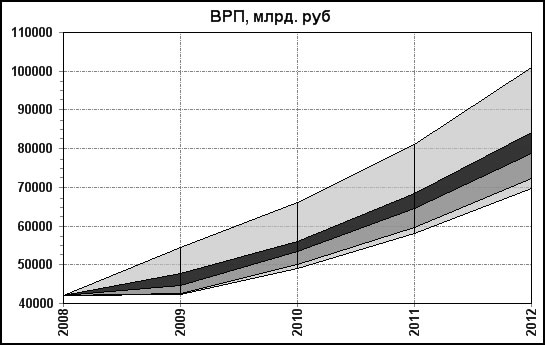
Рис.1. Пошаговое уточнение прогноза показателей ВРП.

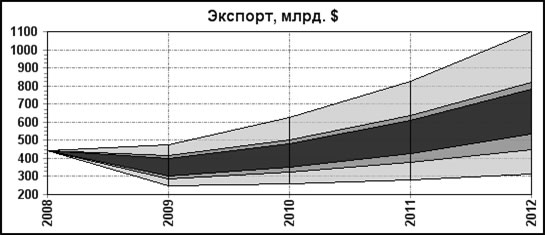
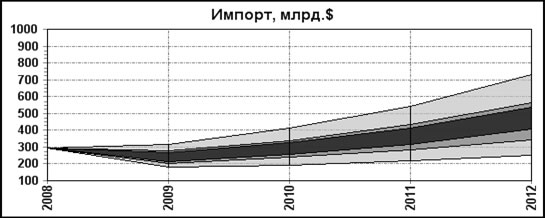
Рис.2. Уточнение экспорта и импорта при пошаговом уточнении ВРП.

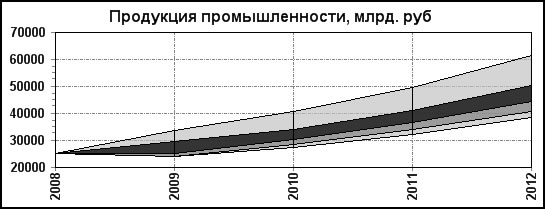
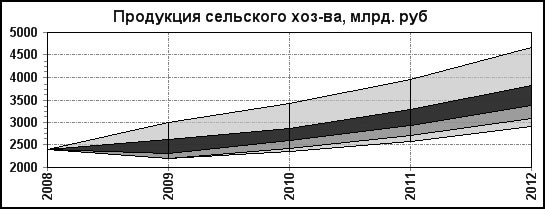
Рис.3. Уточнение отраслевых показателей при пошаговом уточнении ВРП.

7. Резюме. Разработанная технология моделирования при внесении в нее минимальных изменений может быть приспособлена для решения широкого круга задач, оставшихся за пределами нашего рассмотрения. В числе этих задач:

В качестве итога статьи считаем необходимым подчеркнуть следующее. Предшествовавший кризису этап «процветания» был характерен тем, что руководство регионов (и не только их) часто устраивало отсутствие прозрачности в экономике руководимых ими территорий, которое позволяло оперировать функциями управления достаточно свободно. При этом, в частности, бюджет не играл положенной ему роли директивного предписания, а использовался достаточно широко для маневра за счет его статей и внебюджетных фондов.

Кризис существенно усложнил обстановку: доходы бюджета сокращаются, социальная ситуация становится все более напряженной. Рукодство попало в положение капитана, которому в условиях шторма надо иметь достаточно ясное представление как о карте движения, так и о состоянии самого корабля. Чем дальше, тем более становится необходимой та самая прозрачность, которая еще недавно только усложняла «свободу маневра».

Именно такой информационной базой управления может быть только полноценная компьютерная социально-экономическая модель, обеспечивающая возможность как анализа текущего положения, так и реального прогноза последствий тех или иных действий руководства. До последнего времени такой базы просто не было, поскольку традиционная технология моделирования не обеспечивала необходимых возможностей модели, оставляя за ней в условиях низкого качества данных в основном декоративный характер.

Итак, прозрачность ситуации сегодня становится насущно необходимой руководству любого региона как для определения реальных экономических целей и формирования плана, обеспечивающего их достижение, так и для контроля самой системы управления. Пусть эта прозрачность закрыта в сейфе у лица, принимающего решения, но ее отсутствие гарантирует только провал.